算法基础
\(\text{Update: 2024 - 07 - 22}\)
复杂度
定义
衡量一个算法的快慢,一定要考虑数据规模的大小。
一般来说,数据规模越大,算法的用时就越长。
而在算法竞赛中,我们衡量一个算法的效率时,最重要的不是看它在某个数据规模下的用时,而是看它的用时随数据规模而增长的趋势,即时间复杂度。
符号定义
相等是 \(\Theta\),小于是 \(O\),大于是 \(\Omega\)。
大 \(\Theta\) 符号
对于函数 \(f(n)\) 和 \(g(n)\),\(f(n)=\Theta(g(n))\),当且仅当 \(\exists c_1,c_2,n_0>0\),使得 \(\forall n \ge n_0, 0\le c_1\cdot g(n)\le f(n) \le c_2\cdot g(n)\)。
大 \(O\) 符号
\(\Theta\) 符号同时给了我们一个函数的上下界,如果只知道一个函数的渐进上界而不知道其渐进下界,可以使用 \(O\) 符号。\(f(n) = O(g(n))\),当且仅当 \(\exists c,n_0\),使得 \(\forall n \ge n_0,0\le f(n)\le c\cdot g(n)\)。
研究时间复杂度时通常会使用 \(O\) 符号,因为我们关注的通常是程序用时的上界,而不关心其用时的下界。
大 \(\Omega\) 符号
同样的,我们使用 \(\Omega\) 符号来描述一个函数的渐进下界。\(f(n) = \Omega(g(n))\),当且仅当 \(\exists c, n_0\),使得 \(\forall n \ge n_0, 0 \le c \cdot g(n) \le f(n)\)。
主定理
建议背下来,不是很好理解。
\]
那么
\]
需要注意的是,这里的第二种情况还需要满足 \(\text{regularity condition}\), 即 \(a f(n/b) \leq c f(n)\),\(\text{for some constant}\) \(c < 1\) \(\text{and sufficiently large}\) \(n\)。
几个例子:
-
\(T(n) = 2T(\frac{n}{2}) + 1\),那么 \(a = 2, b = 2, {\log_2 2} = 1\),那么 \(\epsilon\) 可以取值在 \((0, 1]\) 之间,从而满足第一种情况,所以 \(T(n) = \Theta(n)\)。
-
\(T(n) = T(\frac{n}{2}) + n\),那么 \(a = 1, b = 2, {\log_2 1} = 0\),那么 \(\epsilon\) 可以取值在 \((0, 1]\) 之间,从而满足第二种情况,所以 \(T(n) = \Theta(n)\)。
-
\(T(n) = T(\frac{n}{2}) + {\log n}\),那么 \(a = 1, b = 2, {\log_2 1} = 0\),那么 \(k\) 可以取值为 \(1\),从而满足第三种情况,所以 \(T(n) = \Theta(\log^2 n)\)。
-
\(T(n) = T(\frac{n}{2}) + 1\),那么 \(a = 1, b = 2, {\log_2 1} = 0\),那么 \(k\) 可以取值为 \(0\),从而满足第三种情况,所以 \(T(n) = \Theta(\log n)\)。
空间复杂度
类似地,算法所使用的空间随输入规模变化的趋势可以用空间复杂度来衡量。
枚举
实际上一些题的正解就是枚举,但需要很多优化。
要点:
-
建立简洁的数学模型。
-
减少不必要的枚举空间。
-
选择合适的枚举顺序。
模拟
模拟即为将题目描述中的操作用代码实现,码量一般比较大,写错比较难调,相当浪费时间。
写模拟题时有以下注意的点:
-
在写代码之前,尽量在演草纸上自习分析题目的实现过程。
-
在代码中尽量把每个部分抽离出来写成函数,模块化。
-
将题目中的信息转化,不要残留多种表达。
-
如果一次没过大样例,分块调试。
-
实现代码时按照演草纸上的思路一步步实现。
递归
定义
我们可以用以下代码理解递归:
long long f(传入数值) {
if(终止条件) return 最小子问题解;
return f(缩小问题规模);
}
递归的优点
- 结构清晰、可读性强,可以参考归并排序的两种实现方式。
- 练习分析为题的结构,当发现问题可以分解成相同结构的小问题时,递归写多了就能敏锐发现这个特点,进而高效解决问题。
递归的缺点
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。而栈不是无限大的,当递归层数过多时,就会造成栈溢出 的后果。
显然有时候递归处理是高效的,比如归并排序;有时候是低效的,比如数孙悟空身上的毛,因为堆栈会消耗额外空间,而简单的递推不会消耗空间。比如这个例子,给一个链表头,计算它的长度:
// 典型的递推遍历框架
int size(Node *head) {
int size = 0;
for (Node *p = head; p != nullptr; p = p->next) size++;
return size;
}
// 我就是要写递归,递归天下第一
int size_recursion(Node *head) {
if (head == nullptr) return 0;
return size_recursion(head->next) + 1;
}
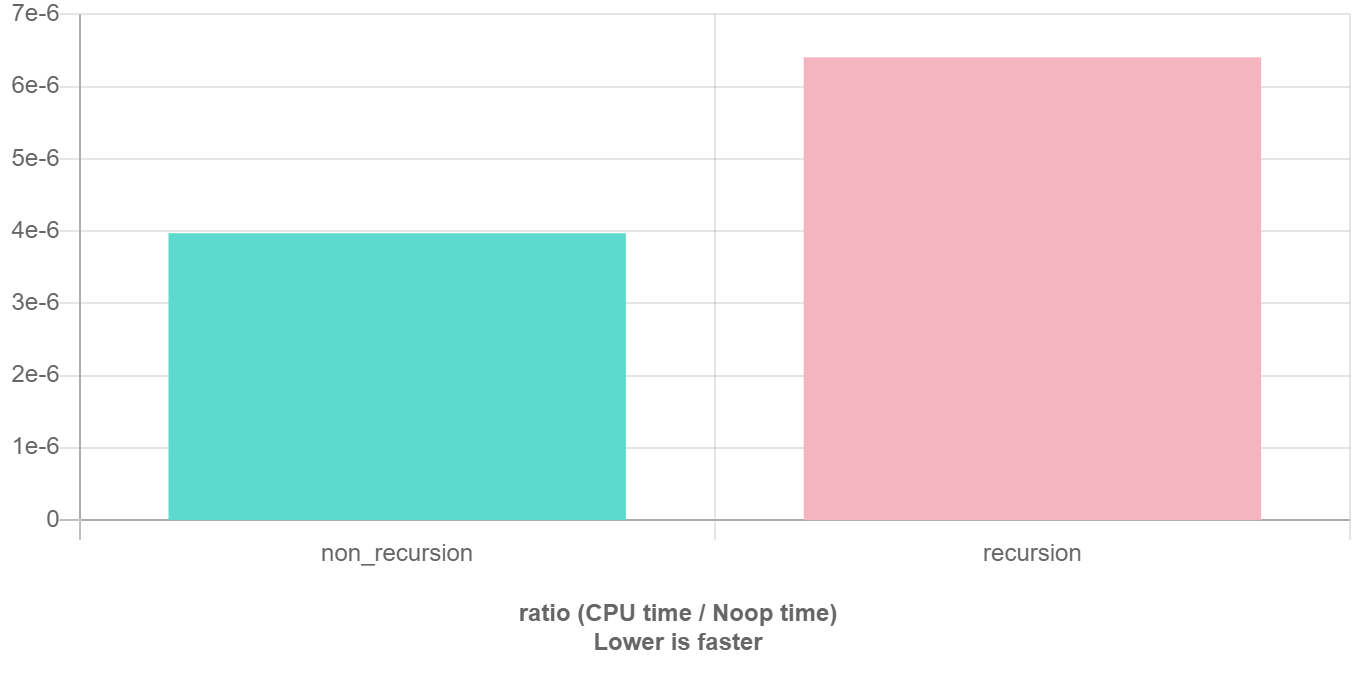
递归优化见后文搜索优化和记忆化搜索。
要点
明白一个函数的作用并相信它能完成这个任务,千万不要跳进这个函数里面企图探究更多细节,否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊。
递归与枚举的区别
枚举是横向地把问题划分,然后依次求解子问题;而递归是把问题逐级分解,是纵向的拆分。
递归与分治的区别
递归是一种编程技巧,一种解决问题的思维方式;分治算法很大程度上是基于递归的,解决更具体问题的算法思想。
分治
定义
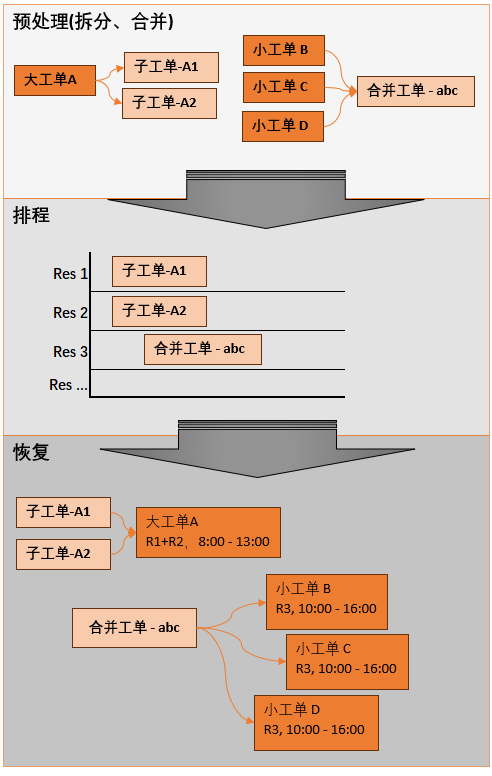
就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
过程
分治算法的核心思想就是「分而治之」。
大概的流程可以分为三步:分解 \(\to\) 解决 \(\to\) 合并。
-
分解原问题为结构相同的子问题。
-
分解到某个容易求解的边界之后,进行递归求解。
-
将子问题的解合并成原问题的解。
分治法能解决的问题一般有如下特征:
-
该问题的规模缩小到一定的程度就可以容易地解决。
-
该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质,利用该问题分解出的子问题的解可以合并为该问题的解。
-
该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
注意:如果各子问题是不独立的,则分治法要重复地解公共的子问题,也就做了许多不必要的工作。此时虽然也可用分治法,但一般用动态规划较好。
贪心
适用范围
贪心算法在有最优子结构的问题中尤为有效。
最优子结构的意思是问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
证明
贪心算法有两种证明方法:反证法和归纳法。
一般情况下,一道题只会用到其中的一种方法来证明。
-
反证法:如果交换方案中任意两个元素/相邻的两个元素后,答案不会变得更好,那么可以推定目前的解已经是最优解了。
-
归纳法:先算得出边界情况(例如 \(n = 1\))的最优解 \(F_1\),然后再证明:对于每个 \(n\),\(F_{n + 1}\) 都可以由 \(F_{n}\) 推导出结果。
常见题型
在提高组难度以下的题目中,最常见的贪心有两种。
-
「我们将 \(XXX\) 按照某某顺序排序,然后按某种顺序(例如从小到大)选择。」。
-
「我们每次都取 \(XXX\) 中最大/小的东西,并更新 \(XXX\)。」(有时「\(XXX\) 中最大/小的东西」可以优化,比如用优先队列维护)
二者的区别在于一种是离线的,先处理后选择;一种是在线的,边处理边选择。
排序解法
用排序法常见的情况是输入一个包含几个(一般一到两个)权值的数组,通过排序然后遍历模拟计算的方法求出最优值。
后悔解法
思路是无论当前的选项是否最优都接受,然后进行比较,如果选择之后不是最优了,则反悔,舍弃掉这个选项;否则,正式接受。如此往复。
排序
几种排序算法的比较
一张表格速通
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 空间 | 稳定性 |
|---|---|---|---|---|---|
| 选择排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 冒泡排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(1)\) | 稳定 |
| 插入排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(n)\) | 稳定 |
| 计数排序 | \(O(n + w)^1\) | \(O(n + w)\) | \(O(n + w)\) | \(O(n + w)\) | 稳定 |
| 基数排序 | \(O(kn + \sum\limits_{i = 1}^{k} w_i)^2\) | \(O(kn + \sum\limits_{i = 1}^{k} w_i)\) | \(O(kn + \sum\limits_{i = 1}^{k} w_i)\) | \(O(n + k)\) | 稳定 |
| 快速排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n^2)\) | \(O(\log n) \sim O(n)\) | 不稳定 |
| 归并排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | 稳定 |
| 堆排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(1)\) | 不稳定 |
| 桶排序 | \(O(n + \frac{n^2}{k} + k)^3\) | \(O(n)\) | \(O(n^2)\) | \(O(n + m)^4\) | 稳定 |
| 希尔排序 | \(O(n \log n) \sim O(n^2)\) | \(O(n^{1.3})\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 锦标赛排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | 稳定 |
| \(\text{tim}\) 排序 | \(O(n \log n)\) | \(O(n)\) | \(O(n \log n)\) | \(O(n)\) | 稳定 |
\(^1\):其中 \(w\) 为排序元素的值域。
\(^2\):其中 \(k\) 为排序元素的最大位数,\(w_i\) 为第 \(i\) 个关键字的值域。
\(^3\):其中 \(k\) 表示将 \(n\) 个元素放进 \(m\) 个桶中,每个桶的数据为 \(k = \frac{n}{m}\)。
\(^4\):其中 \(m\) 表示将 \(n\) 个元素放进的 \(m\) 个桶。
前缀和
定义
前缀和可以简单理解为「数列的前 \(\text{i}\) 项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
一维前缀和
预处理递推式为:
\]
查询 \([l, r]\) 的数值:
\]
二维前缀和
预处理递推式为:
\]
查询 \((i, j) \sim (k, w)\) 的数值:
\]
树上前缀和
设 \(s_i\) 表示结点 \(i\) 到根节点的权值总和。
若是点权,\(x, y\) 路径上的和为 \(s_x + s_y - s_{lca} - s_{fa_{lca}}\)
若是边权,\(x, y\) 路径上的和为 \(s_x + s_y - 2 \times s_{lca}\)
差分
定义
差分是一种和前缀和相对的策略,可以当作是求和的逆运算。
这种策略的定义是令 \(b_i = \begin{cases} a_i - a_{i - 1} \, &i \in[2, n] \\ a_1 \, &i = 1 \end{cases}\)
性质
-
\(a_i\) 的值是 \(b_i\) 的前缀和,即 \(a_n = \sum\limits_{i = 1}^n b_i\)。
-
计算 \(a_i\) 的前缀和 \(sum = \sum\limits_{i = 1}^n a_i = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{i} b_j = \sum\limits_{i = 1}^n (n - i + 1) b_i\)。
它可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。
树上差分
树上差分可以理解为对树上的某一段路径进行差分操作,这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作,并且询问某条边或者某个点在经过操作后的值的时候,就可以运用树上差分思想了。
树上差分通常会结合树基础和最近公共祖先来进行考察。树上差分又分为点差分与边差分,在实现上会稍有不同。
点差分
举例:对树上的一些路径 \(\delta(s_1, t_1), \delta(s_2, t_2), \delta(s_3, t_3)\dots\) 进行访问,问一条路径 \(\delta(s, t)\) 上的点被访问的次数。
对于一次 \(\delta(s, t)\) 的访问,需要找到 \(s\) 与 \(t\) 的公共祖先,然后对这条路径上的点进行访问(点的权值加一),若采用 \(\text{DFS}\) 算法对每个点进行访问,由于有太多的路径需要访问,时间上承受不了。这里进行差分操作:
&d_s\leftarrow d_s + 1\\
&d_{lca}\leftarrow d_{\textit{lca}} - 1\\
&d_t\leftarrow d_t + 1\\
&d_{f(\textit{lca})}\leftarrow d_{f(\textit{lca})} - 1\\
\end{aligned}
\]
其中 \(f(x)\) 表示 \(x\) 的父亲节点,\(d_i\) 为点权 \(a_i\) 的差分数组。
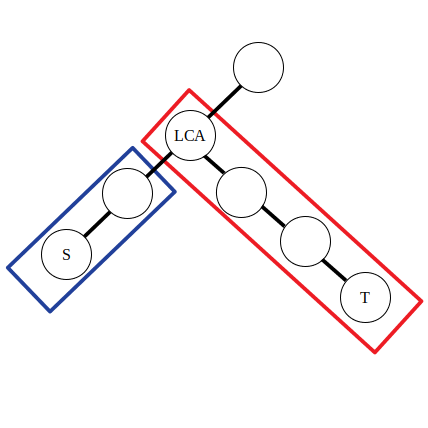
可以认为公式中的前两条是对蓝色方框内的路径进行操作,后两条是对红色方框内的路径进行操作。不妨令 \(\textit{lca}\) 左侧的直系子节点为 \(\textit{left}\)。那么有 \(d_{\textit{lca}} - 1 = a_{\textit{lca}} - (a_{\textit{left}} + 1)\),\(d_{f(\textit{lca})} - 1 = a_{f(\textit{lca})} - (a_{\textit{lca}} + 1)\)。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。
边差分
若是对路径中的边进行访问,就需要采用边差分策略了,使用以下公式:
&d_s\leftarrow d_s + 1\\
&d_t\leftarrow d_t + 1\\
&d_{\textit{lca}}\leftarrow d_{\textit{lca}} - 2\\
\end{aligned}
\]
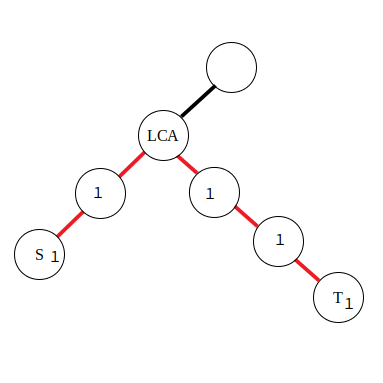
由于在边上直接进行差分比较困难,所以将本来应当累加到红色边上的值向下移动到附近的点里,那么操作起来也就方便了。对于公式,有了点差分的理解基础后也不难推导,同样是对两段区间进行差分。