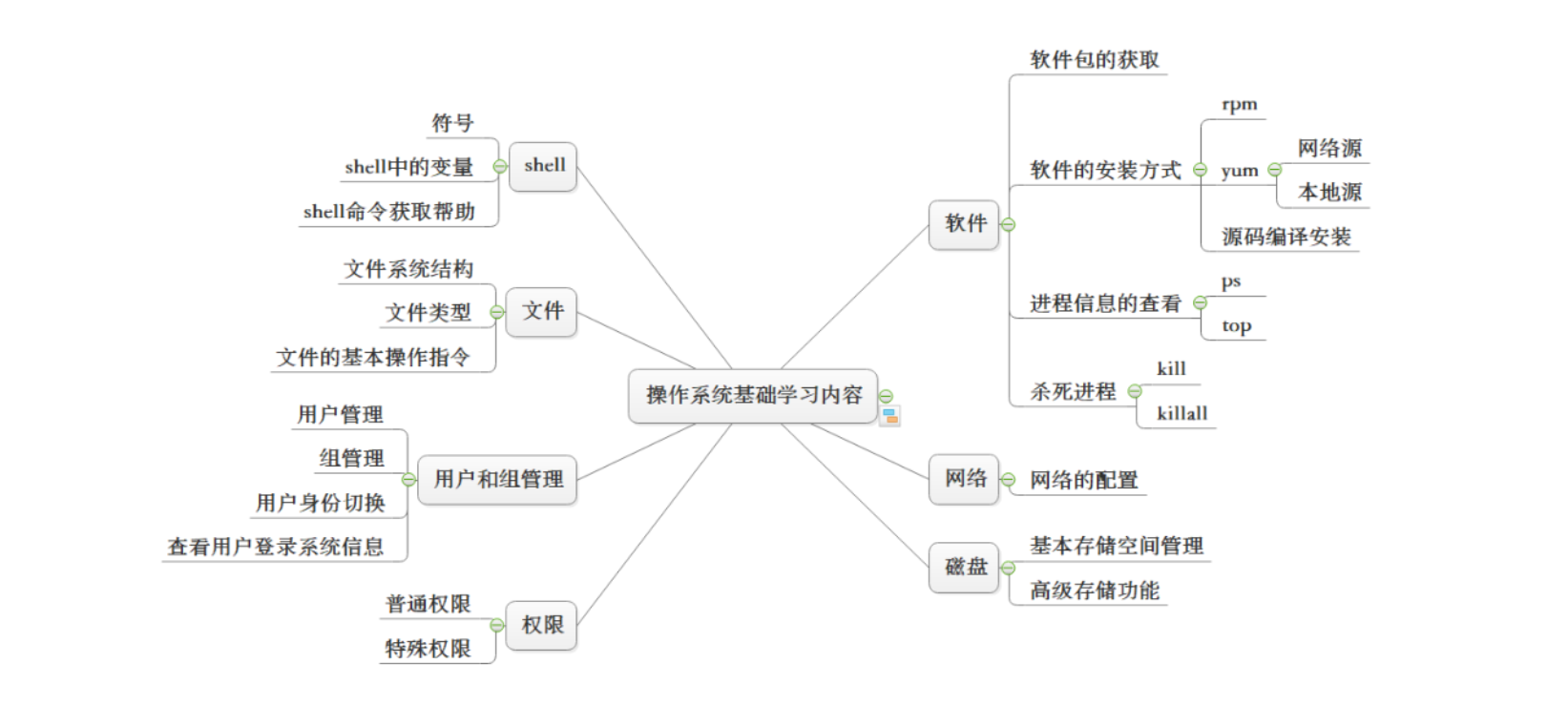
加强堆结构说明
作者:Grey
原文地址:
关于堆和堆排序的说明
可以参考这篇博客:与堆和堆排序相关的问题
基础的堆结构可以实现数据入堆和出堆以后(即: 调用堆的 pop 和 push 方法),使用O(logN)的时间复杂度可以将堆调整好,如果使用的是 Java 语言,可以用 java.util 包中的 PriorityQueue 实现堆的所有操作。
但是,在实际场景中,有一种情况是:在已知的一个堆中,堆中任意一个元素变换后,也要以O(logN)的时间复杂度把堆结构调整正确。这是 Java 语言自带的堆结构(PriorityQueue)无法做到的,这就引入了「加强堆」的概念。「加强堆」提供如下方法
public void resign(T obj) {
}
这个方法表示,对于堆中任意的一个元素 obj,如果调整了其对应的数值,整个堆结构还能在时间复杂度O(logN)下调整好。
普通堆结构之所以无法做到,是因为普通的堆结构没有记录任意一个数据所在的位置信息,所以无法从对应的位置进行堆结构调整。所以,「加强堆」结构引入了一个 HashMap
HashMap<T, Integer> indexMap; // 元素在堆中的位置
有了这个HashMap, 就可以很方便得到某个数据项在堆中的位置是什么,在堆的pop和push方法中,要把HashMap的逻辑加入
public void push(T obj) {
heap.add(obj);
// obj 这个数据在堆中是什么位置
indexMap.put(obj, heapSize);
heapInsert(heapSize++);
}
public T pop() {
T ans = heap.get(0);
swap(0, heapSize - 1);
// 要把对应的obj在堆中直接删除
indexMap.remove(ans);
heap.remove(--heapSize);
heapify(0);
return ans;
}
更重要的是,在堆的 heapify 和 heapInsert 操作中,涉及到的堆中两个元素的交换,也要把堆中元素的位置进行交换。
// 不要忘记把堆中元素的位置也要做交换!!!!
private void swap(int i, int j) {
T o1 = heap.get(i);
T o2 = heap.get(j);
heap.set(i, o2);
heap.set(j, o1);
indexMap.put(o2, i);
indexMap.put(o1, j);
}
以上是铺垫,到了最核心的resign方法,其逻辑如下
public void resign(T obj) {
heapInsert(indexMap.get(obj));
heapify(indexMap.get(obj));
}
整个过程也非常好理解,就是找到变化的那个数据项的位置,然后执行heapify和heapInsert,由于变换过程无非是变大或者变小,所以找到变换的位置,heapify和heapInsert操作只会执行一个操作!另外一个操作进去以后会直接跳出。
加强堆的完整代码如下(支持泛型):
import java.util.ArrayList;
import java.util.Comparator;
import java.util.HashMap;
import java.util.List;
public class Code_CustomHeap {
// 自己手写堆
public static class HeapGreater<T> {
private ArrayList<T> heap;
private HashMap<T, Integer> indexMap; // 元素在堆中的位置
private int heapSize; // 和heap配合使用
private Comparator<? super T> comp;
public HeapGreater(Comparator<T> c) {
heap = new ArrayList<>();
indexMap = new HashMap<>();
comp = c;
}
public boolean isEmpty() {
return heapSize == 0;
}
public int size() {
return heapSize;
}
public boolean contains(T obj) {
return indexMap.containsKey(obj);
}
public T peek() {
return heap.get(0);
}
public void push(T obj) {
heap.add(obj);
indexMap.put(obj, heapSize);
heapInsert(heapSize++);
}
public T pop() {
T ans = heap.get(0);
swap(0, heapSize - 1);
indexMap.remove(ans);
heap.remove(--heapSize);
heapify(0);
return ans;
}
public void remove(T obj) {
T replace = heap.get(heapSize - 1);
int index = indexMap.get(obj);
indexMap.remove(obj);
heap.remove(--heapSize);
if (obj != replace) { // obj == replace表示删掉的是最后一个位置的数据,此时不需要进行resign操作
heap.set(index, replace);
indexMap.put(replace, index);
resign(replace);
}
}
public void resign(T obj) {
heapInsert(indexMap.get(obj));
heapify(indexMap.get(obj));
}
// 请返回堆上的所有元素
public List<T> getAllElements() {
List<T> ans = new ArrayList<>();
for (T c : heap) {
ans.add(c);
}
return ans;
}
private void heapInsert(int index) {
while (comp.compare(heap.get(index), heap.get((index - 1) / 2)) < 0) {
swap(index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private void heapify(int index) {
int left = index * 2 + 1;
while (left < heapSize) {
int best =
left + 1 < heapSize && comp.compare(heap.get(left + 1), heap.get(left)) < 0
? (left + 1)
: left;
best = comp.compare(heap.get(best), heap.get(index)) < 0 ? best : index;
if (best == index) {
break;
}
swap(best, index);
index = best;
left = index * 2 + 1;
}
}
private void swap(int i, int j) {
T o1 = heap.get(i);
T o2 = heap.get(j);
heap.set(i, o2);
heap.set(j, o1);
indexMap.put(o2, i);
indexMap.put(o1, j);
}
}
}
使用加强堆来解决的问题示例,见使用加强堆解决 topK 问题

















![[Java]线程生命周期与线程通信](https://img-blog.csdnimg.cn/direct/8e1a396ad6f2425a8bea15c5fe54c1f3.png)