数组分成两个最接近集合问题
作者:Grey
原文地址:
问题描述
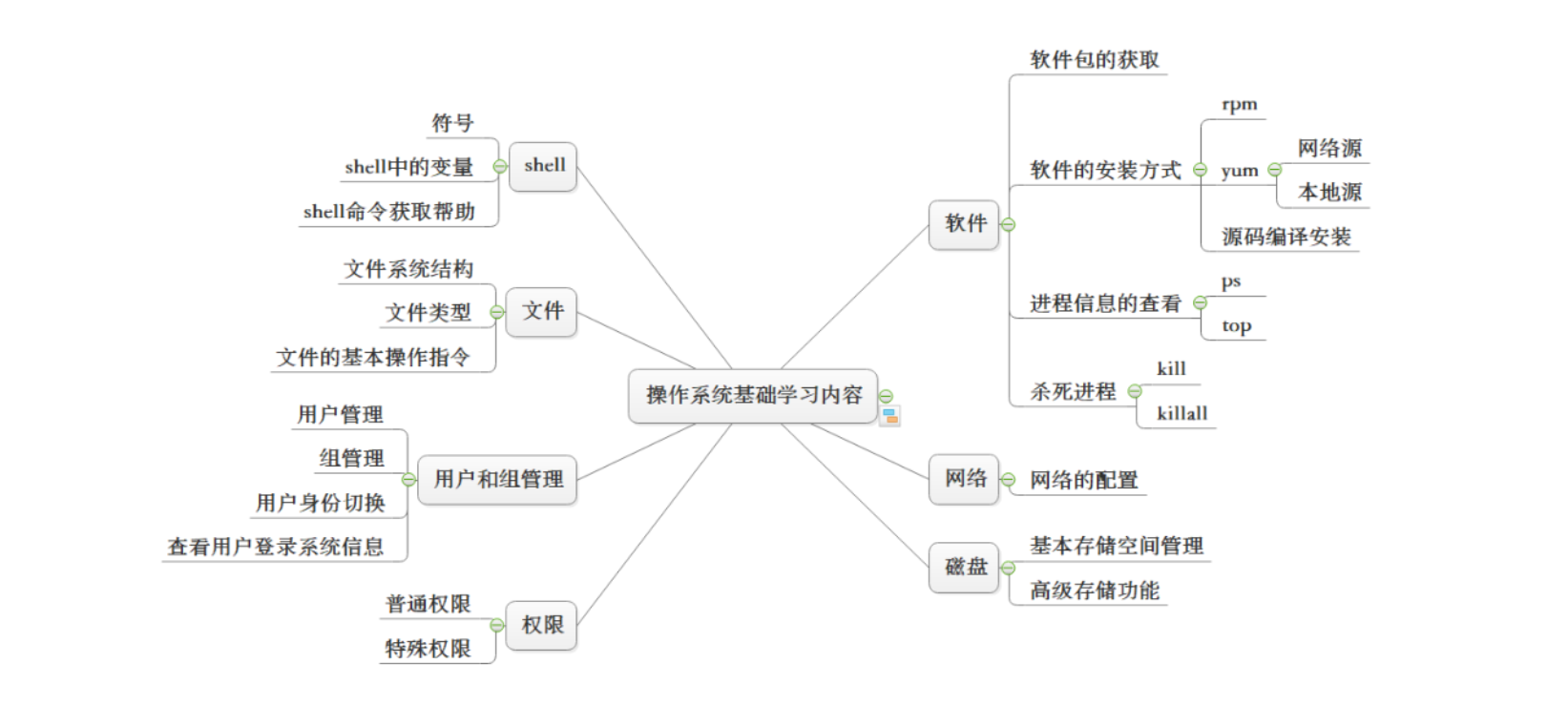
给定一个正数数组 arr, 请把 arr 中所有的数分成两个集合,尽量让两个集合的累加和接近;
返回:最接近的情况下,较小集合的累加和。
主要思路
首先把数组之和求出来,假设为 sum,那么sum/2就是累加和的一半,定义递归函数
int process(int[] arr, int i, int rest)
递归含义表示:数组 arr 从 i 开始,一直到最后,随意选取进行累加,得到的最接近 rest 且较小的集合的累加和。
接下来是 base case,i 到数组 arr 的结尾位置,显然返回 0。
if (i == arr.length) {
return 0;
}
接下来是普遍位置
int p1 = process(arr, i + 1, rest);
if (rest - arr[i] >= 0) {
p1 = Math.max(process(arr, i + 1, rest - arr[i]) + arr[i], p1);
}
其中 p1 表示:不选取 i 位置的值进行累加,得到的最接近 rest 且较小的集合的累加和。
process(arr, i + 1, rest - arr[i]) + arr[i]表示:选取了 i 位置的值进行累加,得到的最接近 rest 且较小的集合的累加和。
注:选取 i 位置的值进行累加有条件,即rest - arr[i] > 0,否则选取之后,会得到较大的那个集合的累加和。
递归方法的完整代码见(含对数器)
public static int splitSumClosed(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int num : arr) {
sum += num;
}
int aim = sum / 2;
return process(arr, 0, aim);
}
public static int process(int[] arr, int i, int rest) {
if (i == arr.length) {
return 0;
}
int p1 = process(arr, i + 1, rest);
if (rest - arr[i] >= 0) {
p1 = Math.max(process(arr, i + 1, rest - arr[i]) + arr[i], p1);
}
return p1;
}
以上暴力递归可以改成动态规划,由于递归函数的可变参数有两个,一个是 i,一个是 rest,且其变化范围是固定的,所以可以定义一个二维数组来存所有的递归过程值,
int[][] dp = new int[arr.length + 1][aim + 1];
接下来根据递归函数可知dp表的最后一行均为 0;
且dp[i][rest]依赖于dp[i+1][rest]和dp[i+1][rest - arr[i]]两个位置的值,所以整个 dp 表可以从最后一行开始依次往上递推。
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = 0; j < aim + 1; j++) {
int p1 = dp[i + 1][j];
if (j - arr[i] >= 0) {
p1 = Math.max(dp[i + 1][j - arr[i]] + arr[i], p1);
}
dp[i][j] = p1;
}
}
动态规划方法完整代码如下
public static int splitSumClosed2(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
int sum = 0;
for (int num : arr) {
sum += num;
}
int aim = sum / 2;
int[][] dp = new int[arr.length + 1][aim + 1];
// last row == 0
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = 0; j < aim + 1; j++) {
int p1 = dp[i + 1][j];
if (j - arr[i] >= 0) {
p1 = Math.max(dp[i + 1][j - arr[i]] + arr[i], p1);
}
dp[i][j] = p1;
}
}
return dp[0][aim];
}


















![[Java]线程生命周期与线程通信](https://img-blog.csdnimg.cn/direct/8e1a396ad6f2425a8bea15c5fe54c1f3.png)