【信息论】信息熵、损失熵、噪声熵和互信息量
原文链接:https://www.cnblogs.com/Baiyug/p/16908846.html
1 信息熵
信息熵(entropy)表征了某个信息的平均不确定度,是信息自信息量的数学期望。例如,某个信源发出L个信息序列(即L个信息符号),每个信息符号的取值有m个
X_i \in \{a_1,a_2,a_3,...,a_i,...a_m\}
\]
这里的 \(X_i\) 是个抽象的概念,实际上一个符号就代表一个码元,每个码元由比特位构成,也就是由0,1序列构成。
怎么理解\(a_i\)?
\(a_i\) 就是每个信息符号\(X_i\)可能取的值,比如说001,010或111等等,注意,一个信息符号只能取一个\(a_i\)。
看个例题
接着上面那个例子,我们讨论第一个信息符号,假设\(X_1\)的概率空间有
\[p(X_1) = p(a_i) =
\begin{bmatrix}
\frac{1}{2} && \frac{1}{3} && \frac{1}{6}
\end{bmatrix}\\
\]即,\(X_1\)这个符号可能取为\(a_1\),\(a_2\)或\(a_3\),并且各个取值的概率为
\[p(a_1) = \frac{1}{2}\\
p(a_2) = \frac{1}{3}\\
p(a_3) = \frac{1}{6}\\
\]我们求信息符号 \(X_1\) 的熵,用\(H(X_1)\)表示
计算结果如下
\[\begin{aligned}
H(X_1)&= E(I(a_i)) \\
&= \sum_{i=1}^{3} p(a_i)log_2\frac{1}{p(a_i)}\\
&= -\frac{1}{2}log_2(\frac{1}{2})-\frac{1}{3}log_2(\frac{1}{3})-\frac{1}{6}log_2(\frac{1}{6})\\
&\approx 1.46 (bit/符号)
\end{aligned}
\]
这是一个信息符号的熵,仅描述了一个信息符号的平均不确定度,要讨论一个信息序列的熵,则要更复杂一些,一般的对于无记忆信源,其信息序列的熵就是各个单符号信息熵的和;对于有记忆信源,其信息序列的熵的计算方法就比较复杂,这里不做讨论。
总之,符号信息熵表征为符号信息的平均不确定度,能够代表该符号所携带的信息量,或者说表示为符号携带的信息量的期望值。其值越大,表示符号最有可能携带的信息量越大。
符号信息熵不能无穷大,即存在最大值,当该符号的各个取值的概率相等时,即取值等概分布的条件下,符号信息熵取得最大值,
\]
\(M\)表示符号能够取值的个数,在上面那个例子中,\(M\) 就是\(a\)的个数,即 \(M = 3\),所以在上述例子中,
\[H(X)_{max} = log_2 3 \approx 1.58(bit/符号)
\]
2 有噪有损信道模型
信息传输中,一个重要的步骤就是经过信道,在信道中,我们传输的信息可能会受到干扰(即环境噪声会影响我们的有效信息),另外,我们要传输的信息可能会在信道中损失。下面我用图解的方法给出一个单符号信息在有噪有损信道传输的模型。
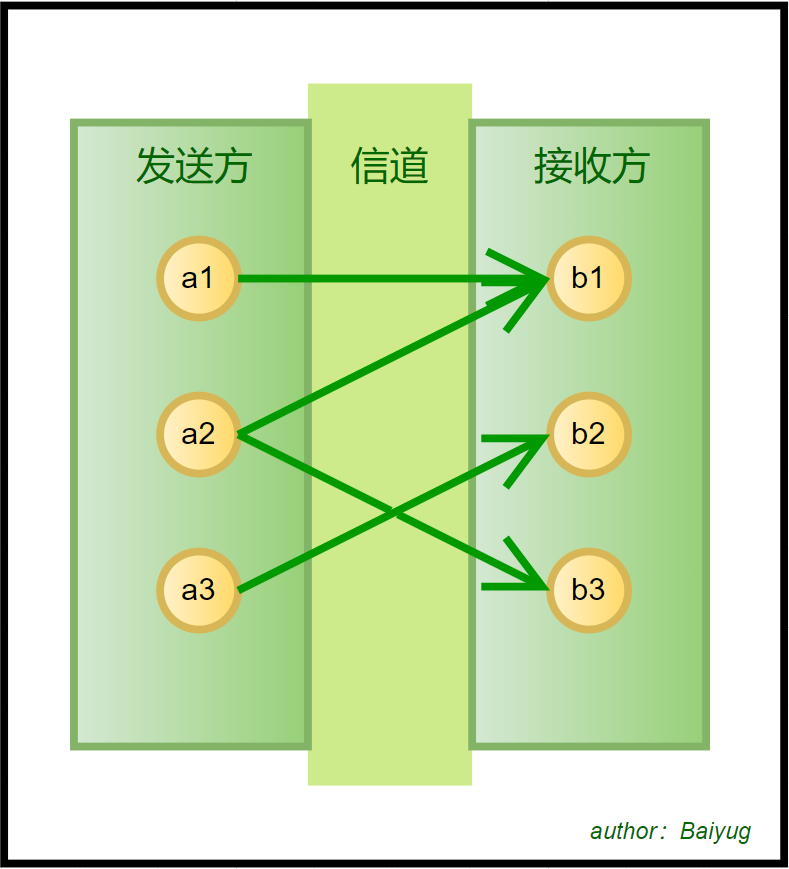
可以看到,发送端如果发送的是\(a_2\),那么接收端有可能收到\(b_1\),也可能收到\(b_3\),这是因为噪声的干扰;再看接收端,如果收到的是\(b_1\),那么对应的发送端有可能是\(a_1\),也可能是\(a_2\),这代表\(a_1\)或者\(a_2\)发送的信息有一定的损失。
3 图解信息熵、损失熵、噪声熵和互信息的关系
在上述的有噪有损信道中传输信息,涉及的信息量可以分成几类,
- 发送端的期望信息量,表示为\(H(X)\),即发送端的信息熵
- 接收端的期望信息量,表示为\(H(Y)\),即接收端的信息熵
- 传输中损失的期望信息量,表示为\(H(X|Y)\),即损失熵,又叫疑义度
- 噪声包含的期望信息量,表示为\(H(Y|X)\),即噪声熵
- 在信道中传输的期望信息量,表示为\(I(X;Y)\),即联系发送端与接收端的平均互信息量
话不多说,直接上图
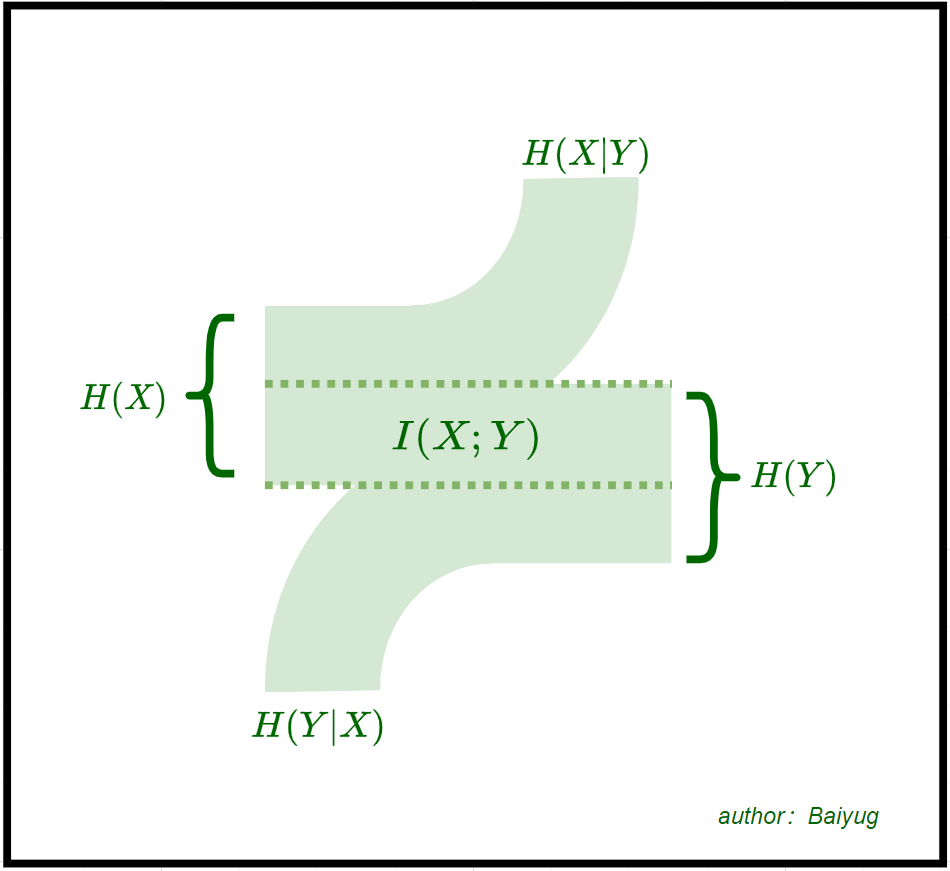
上图参考了一些其他的资料,从该图,我们可以形象的描述信息熵、损失熵、噪声熵和互信息之间的数量关系,并且理解什么叫损失,什么叫噪声干扰。







![[软件体系结构/架构]零拷贝技术(Zero-copy)[转发]](https://img2023.cnblogs.com/blog/1173617/202303/1173617-20230328135340551-1546815055.png)

![[Qt基础内容-08] Qt中MVC的M(Model)](https://img-blog.csdnimg.cn/img_convert/4f2ca75a9f193cca7544514bb980f8c2.jpeg)









