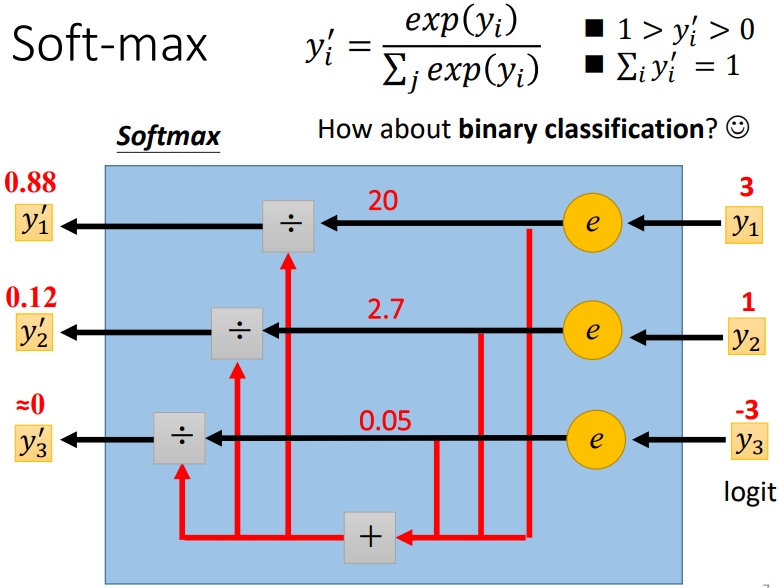
softmax求导的过程-小白菜博客
（图出自李宏毅老师的PPT）

对机器学习/深度学习有所了解的同学肯定不会对 softmax 陌生，它时而出现在多分类中用于得到每个类别的概率，时而出现在二分类中用于得到正样本的概率（当然，这个时候 softmax 以 sigmoid 的形式出现）。

1. 从 sigmoid 到 softmax

sigmoid 出现的频率在机器学习/深度学习中不可谓不高，从 logistic 回归到深度学习中的激活函数。先来看一下它的形式：

\[sigmoid(z) = \sigma(z) = \frac{1}{1 + e^{-z}}, \:\:\:\: z \in \mathbb{R}
\]

我们把它的图像画一下：

import numpy as np
imort matplotlib.pyplot as plt

x = np.arange(-5, -5, 0.05)
z = x / (1 + np.exp(-x))

plt.plot(x, z)
plt.show()

softmax求导的过程-小白菜博客
显然，sigmoid 将实数域的值压缩到了 \((0, 1)\) 之间。那么在二分类中又是怎么用的呢？以 logistic 回归为例。在逻辑回归中通常假设样本的类别呈现为伯努利分布，即：

\[P(y=1) = p_1 \\
P(y=0) = p_0
\]

且有 \(p_1 + p_0 = 1\)。用逻辑回归解决二分类问题时，我们用建模的时样本为正样本的概率（根据伯努利分布，为负样本的概率显而易见）：将逻辑回归得到的回归值输入到 sigmoid 中就得到了 \(p_1\)，即：

\[z = f(z) \\
p_1 = \frac{1}{1 + e^{-z}}
\]

其中 \(f\) 即是一个回归函数。那么 sigmoid 又与 softmax 有什么关系呢？先来看一下 softmax 的定义：

\[softmax(\mathbf{z}) = \frac{e^{\mathbf{z}}}{\sum_{i}^{n} e^{z_i}}, \:\:\:\: \mathbf{z} \in \mathbb{R}^n
\]

显然，softmax 是一个向量的函数，正如本文开头的图示一样。softmax 将一个向量中的值进行了归一化，我们在多分类中常将其视作样本属于不同类别的概率值。我们将设有一个二分类模型，其输出是一个向量 \(\mathbf{z} \in \mathbb{R}^2\)，其中 \(z_0, z_1\) 分别是样本属于类别 0, 1 的未归一化的值。如果我们用 \(softmax\) 得到类别概率，则：

\[p_0 = \frac{e^{z_0}}{e^{z_0} + e^{z_1}} \\
p_1 = \frac{e^{z_1}}{e^{z_0} + e^{z_1}}
\]

\(p_0, p_1\) 即是样本分别属于 0, 1 的概率，我们对其进行以下变形：

\[\begin{aligned}
p_1 &= \frac{e^{z_1}} {e^{z_0} + e^{z_1}} \\
&= \frac{e^{z_1}} {e^{z_0}( e^{z_0 - z_0} + e^{z_1 - z_0} )} \\
&= \frac{e^{z_1 - z_0}} {e^{z_0 - z_0} + e^{z_1 - z_0} } \\
&= \frac{e^\Delta} {e^{0} + e^{\Delta}} \\
&= \frac{e^\Delta} {1 + e^{\Delta}} \\
&= \frac{1} {1 + e^{-\Delta}}
\end{aligned}
\]

其中 \(\Delta = z_1 - z_0\)，同理可得 \(p_0 = \frac{1} {e^{\Delta} + 1}\)。回想到逻辑回归是对样本属于 1 概率进行建模，那么 \(\Delta\) 就是逻辑回归进入 sigmoid 之前的预测值，这里我们来看看 \(\Delta\) 到底是什么：

\[\frac{p_1} {p_0} = \frac{1} {e^\Delta} = e^{\Delta} \\
\log \frac{p_1} {p_0} = \Delta
\]

由上可知，逻辑回归是对样本为 1 和 为 0 的概率的比值（几率）的对数（对数几率）进行回归。所以说逻辑回归也是一种回归，只不过回归的是样本的对数几率，得到了对数几率后再来得到样本属于类别 1 的概率。

再说回 sigmoid 和 softmax 的关系，其实从上面的的世子我们也看出来了其实 sigmoid 只是 softmax 的一种情况，sigmoid 隐式地包含了另一个元素地 softmax 值。在对分类任务进行建模时，我们通常将二分类任务中的一个类别进行建模，假设其服从伯努利分布；或者建模为二项分布，分别建模样本属于每个类别地概率（即 \(\mathbf{z}\) 中的每一位表示样本为对应类别的对数几率，\(softmax(\mathbf{z})\) 中的每一位表示样本为对应类别的概率）。

2. softmax 损失的求导

在多分类任务中，我们通常使用对数损失（在二分类中就是交叉熵损失）：

\[\mathcal{L} = -\frac{1} {N} \sum_{i=1}^N \sum_{j=1}^C y_{ij} \log \hat{y}_{ij}
\]

其中，\(N, C\) 分别为样本数和类别数，\(y_{ij} \in \{0, 1\}\) 表示样本 \(x_i\) 是否属于类别 \(j\)，\(\hat{y}_{ij}\) 表示对应的预测概率。在多分类中，概率值通常通过 softmax 获得，即：

\[\hat{y}_{ij} = softmax(\mathbf{z}_i)_j = \frac{e^{z_{ij}}} {\sum_{k=1}^C e^{z_{ik}}}
\]

这里我们只考虑一个样本的损失，即：

\[\mathcal{l} = -\sum_{j=1}^C y_{j} \log \hat{y}_{j} \\
\hat{y}_{j} = softmax(\mathbf{z})_j = \frac{e^{z_{j}}} {\sum_{k=1}^C e^{z_{k}}}
\]

好了，开始重头戏，求多分类对数损失对 \(z_k\) 的偏导：

\[\begin{aligned}
\frac{\partial \mathcal{l}} {\partial z_k} &= - \frac{\partial} {\partial z_k} (\sum_{j=1}^C y_{j} \log \hat{y}_{j}) \\
&= - \sum_{j=1}^C y_{j} \frac{\partial \log \hat{y}_{j}} {\partial z_k} \\
&= - \sum_{j=1}^C y_{j} \frac{1} {\hat{y}_j} \frac{\partial \hat{y}_j} {\partial z_k}
\end{aligned}
\]

到这里其实以及很简单了，只需要算出 \(\frac{\partial \hat{y}_j} {\partial z_k}\) 就行了，那就来吧：

\[\begin{aligned}
\frac{\partial \hat{y}_j} {\partial z_k} &= \frac{\partial} {\partial z_k} (\frac{e^{z_j}} {\sum_{c=1}^C e^{z_c}}) \\
&= \frac{\frac{\partial e^{z_j}} {\partial z_k} \cdot \sum - e^{z_j} \cdot \frac{\partial \sum} {\partial z_k} } {(\sum)^2} \\
&= \frac{\frac{\partial e^{z_j}} {\partial z_k} \cdot \sum - e^{z_j} \cdot e^{z_k} } {(\sum)^2}
\end{aligned}
\]

其中 \(\sum = \sum_{c=1}^C e^{z_c}\)，其中 \(\frac{\partial e^{z_j}} {\partial z_k}\) 需要分情况讨论一下：

\[\frac{\partial e^{z_j}} {\partial z_k} =
\begin{cases}
e^{z_j} & k = j \\
0 & k \neq j
\end{cases}
\]

因此，

\[\frac{\partial \hat{y}_j} {\partial z_k} =
\begin{cases}
\frac{e^{z_j}\ \cdot \ \sum - (e^{z_j})^2 } {(\sum)^2} & k = j \\
\frac{0 \cdot \sum - e^{z_j} \cdot e^{z_k} } {(\sum)^2} & k \neq j
\end{cases}
\]

看起来有点复杂，我们来化简以下：

\[\frac{\partial \hat{y}_j} {\partial z_k} =
\begin{cases}
\hat{y}_j (1 - \hat{y}_j) & k = j \\
- \hat{y}_j \cdot \hat{y}_k & k \neq j
\end{cases}
\]

收工了吗？不！我们的目的是求 \(\frac{\partial \mathcal{l}} {\partial z_k}\)：

\[\begin{aligned}
\frac{\partial \mathcal{l}} {\partial z_k} &= -[y_k \frac{1} {\hat{y}_k} \frac{\partial \hat{y}_k} {\partial z_k} + \sum_{j \neq k} y_j \frac{1} {\hat{y}_j} \frac{\partial \hat{y}_j} {\partial z_k} ] \\
&= -[y_k \frac{1} {\hat{y}_k} \cdot \hat{y}_k (1 - \hat{y}_k) + \sum_{j \neq k} y_j \frac{1} {\hat{y}_j} \cdot (- \hat{y}_j \cdot \hat{y}_k) ] \\
&= -[y_k \cdot (1 - \hat{y}_k) - \sum_{j \neq k} y_j \cdot \hat{y}_k ] \\
&= -[y_k - y_k \cdot \hat{y}_k - \sum_{j \neq k} y_j \cdot \hat{y}_k ] \\
&= -[y_k - \sum_{j} y_j \cdot \hat{y}_k ] \\
&= \sum_{j} y_j \cdot \hat{y}_k - y_k \\
&= \hat{y}_k \cdot \sum_{j} y_j - y_k \\
&= \hat{y}_k - y_k
\end{aligned}
\]

别看求起来有一点复杂，但是最后的结果还是很优雅的嘛：预测值 - 真实值。

这里有几个要注意的点：

  • 上式第二部中依据 \(j\) 是否等于 \(k\) 将求和分成了两部分；
  • 上式的倒数第二步中，利用了多分类的目标中只有一个为 1，即 \(\sum_j y_j = 1\).

以上！