算法学习笔记（数学）：数论分块 + 容斥原理 + 莫比乌斯函数

这篇文章主要是要讲一道题目（链接在这里)
以及梳理一下数论分块，莫比乌斯函数，容斥原理这些知识。
先介绍下知识点吧qwq

数论分块

想必大家一定学过数据结构中的分块操作吧，通过\(sqrt(n)\)的区间分块去提高暴力的效率，其实数列分块在本质上与其是有异曲同工之妙的，大家可以先来想想这个问题：

\[\sum_{i = 1}^{n}\left \lfloor \frac{n}{i}\right \rfloor = ?
\]

对于这个问题，我们可以手动去模拟一下，比方说取\(n=9\)，遍历一遍\(i\)的取值，会发现\(\left \lfloor \frac{n}{i}\right \rfloor\)的值其实是很少的，所以我们也可以像分块一样去帮他们分成几个区间去操作处理。那么怎么分呢，我们可以定义这个式子成立\(\left \lfloor \frac{n}{x}\right \rfloor = \left \lfloor \frac{n}{g(x)}\right \rfloor\),然后令\(g(x)\)为当前等式成立的情况下,\(x\)最大的取值。
先讲结论:\(g(x) = \left \lfloor \frac{n}{\left \lfloor \frac{n}{x}\right \rfloor}\right \rfloor\)
证明：令\(k = \left \lfloor \frac{n}{x}\right \rfloor\)，则\(\left \lfloor\frac{n}{k} \right \rfloor >= \left \lfloor \frac{n}{\left \lfloor \frac{n}{x}\right \rfloor}\right \rfloor >= \left \lfloor x\right \rfloor = x\)，所以我们就知道\(x\)最大的时候的取值了。
再证明 \(\left \lfloor\frac{n}{\left \lfloor \frac{n}{x}\right \rfloor} \right \rfloor = \left \lfloor \frac{n}{x}\right \rfloor\)
贴一下y总的证明过程(思路还是比较简单的，证明一个大于等于和一个小于等于同时成立，所以等号成立)
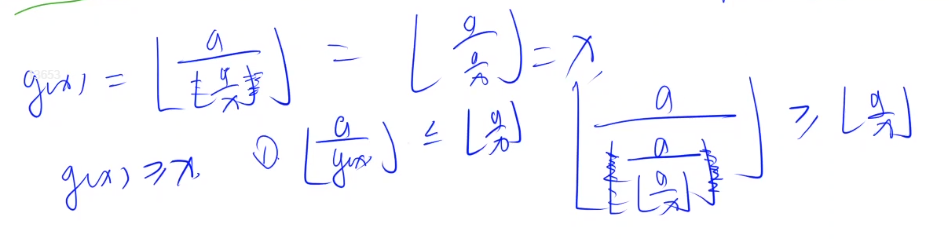
算法学习笔记（数学）：数论分块 + 容斥原理 + 莫比乌斯函数-小白菜博客
复杂度：
我们可以这么考虑复杂度，对于\(\frac{n}{i}\)，当\(i <= sqrt(n)\)时，从\((1,sqrt(n))\)是只最多只有\(sqrt(n)\)个值的，因为最多的情况就是每次除都会有新的值出现。同理，大于\(sqrt(n)\)时\(n / i <= sqrt(n)\)所以最多也只有根号种取值。
所以最多有\(2*sqrt(n)\)段，复杂度\(O(sqrt(n))\)。
然后我们就可以像数列分块一样，在\(O(sqrt(n))\)的复杂度去计算前面的式子啦。

莫比乌斯函数 + 容斥原理

这两个知识放在一起讲是因为其关联性还是比较大的。
比方说这个问题是求\(gcd(x,y) = 1,(x <= a,y <= b)\)的对数是，我们很自然的可以想到容斥原理，要求的对数就等于总对数减去不合理对数，所以我们可以列出这样的一条公式：\(ans =a*b - a/2*b/2 -a/3 *b/3-a/5*b/5....+a/6*b/6.....\)
标准的容斥原理公式啦！
那么莫比乌斯函数是干啥的呢，定义如下：

\[\mu (x)=\left\{\begin{matrix}
& 0 &\exists \alpha >1 \\
& (-1)^{k} & k为质因数分解项数 \\
& 1 & x=1 \\
\end{matrix}\right.\]

那么我们上面那条标准的式子是不是就可以进一步化简了？
化简式子如下:

\[\sum_{i=1}^{min(a,b)}\left \lfloor \frac{a}{i}\right \rfloor*\left \lfloor \frac{b}{i}\right \rfloor*\mu(i)
\]

然后我们就可以发现，可以用数论分块来加速这条式子哩。于是我们就可以切掉这道题了（链接在文章开头)

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long long ll;
#define int long long
#define endl '\n' 
typedef pair<int, int> PII;
const int N = 5e4 + 20;
const int Inf = 0x3f3f3f3f3f3f3f3f;
const int mod = 1e9 + 7;
int primes[N];
int mobius[N];
bool st[N];
int cnt;
int sum[N];
void init(int n) {
	mobius[1] = 1;
	for (int i = 2;i <= n;i ++) {
		if(!st[i]){
			primes[cnt++] = i;
			mobius[i] = -1; 
		}
		for (int j = 0;primes[j] * i <= n;j ++) {
			st[primes[j] * i] = true;
			if(i % primes[j] == 0) {
				mobius[i * primes[j]] = 0;
				break;
			}
			mobius[i * primes[j]] = mobius[i] * -1;
		}
	}
	for (int i = 1;i <= n;i ++) sum[i] = sum[i - 1] + mobius[i];
}

void solve(){
	int a,b,d;
	cin >> a >> b >> d;
	a = a / d;
	b = b / d;
	int n = min(a,b);
	int ans = 0;
	for (int l = 1,r;l <= n;l = r + 1) {
		r = min(n , min(a / (a/ l),b / (b / l))); // 不能超过n
		ans = ans + (sum[r] - sum[l - 1]) * (a / l) * (b / l); // 这里 a / l 和 b / l 是相同的，所以式子提取出来，就可以用莫比乌斯函数的前缀和了
	}
	cout << ans << endl;
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);cout.tie(nullptr);
	int t;
	init(N);
	cin >> t;
	while (t--) solve();
	// solve(); 
    return 0;
}

qwq希望这样的整理能有点用（latex公式确实很难打）
image