CHANGE LOG
- 2021.12.25:新增 ACAM 部分。
- 2021.12.26:新增 SAM 部分。
- 2022.2.9:计划重构文章。
- 2022.2.20:重构完成,增加部分例题。
基本定义与约定:
- 称字符串 \(T\) 匹配 \(S\) 为 \(T\) 在 \(S\) 中出现。
- 模式串:相当于题目给出的 字典,用于匹配的字符串。下文也称 单词。
- 文本串:被匹配的字符串。
- 更多约定见 常见字符串算法。
1. AC 自动机 ACAM
前置知识:字典树,KMP 算法与 动态规划 思想。
AC 自动机是一类确定有限状态自动机,这说明它有完整的 DFA 五要素,分别是起点 \(s\)(Trie 树根节点),状态集合 \(Q\)(Trie 树上所有节点),接受状态集合 \(F\)(所有以某个单词作为后缀的节点),字符集 \(\Sigma\)(题目给定)和转移函数 \(\delta\)(类似 KMP 求解)。
AC 自动机全称 Aho-Corasick Automaton,简称 ACAM。它的用途非常广泛,是重要的字符串算法(\(8\) 级)。
1.1 算法详解
AC 自动机用于解决 多模式串 匹配问题:给定 字典 \(s\) 和文本串 \(t\),求每个单词 \(s_i\) 在 \(t\) 中出现的次数。当然,它的实际应用十分广泛,远超这一基本问题。ACAM 与 KMP 的不同点在于后者仅有一个模式串,而前者有多个。
朴素的基于 KMP 的暴力时间复杂度为 \(|t|\times N + \sum |s_i|\),其中 \(N\) 是单词个数。因为进行一次匹配的时间复杂度为 \(|s_i| + |t|\)。当单词数量 \(N\) 较大时,无法接受。
多串问题自然首先考虑建出字典树。根据其定义,字典树上任意节点 \(q\in Q\) 与所有单词的某个前缀 一一对应。设节点(节点也称状态)\(i\) 表示的字符串为 \(t_i\)。
借鉴 KMP 算法的思想,我们考虑对于每个状态 \(q\),求出其 失配指针 \(fail_q\)。类似 KMP 的失配数组 \(nxt\),失配指针的含义为:\(q\) 所表示字符串 \(t_q\) 的 最长真后缀 \(t_q[j, |t_q|]\ (2\leq j\leq |t_q| + 1)\),使得该后缀作为某个单词的前缀出现。这说明 \(t_q[j, |t_q|]\) 恰好对应了字典树上某个状态,因此一个状态的失配指针指向另一个长度比它短的状态。注意,这样的后缀 可能不存在,因此失配指针可能指向表示空串的根节点。
从 \(q\) 向字符串 \(fail_q\) 连一条有向边,就得到了 ACAM 的 fail 树。
- 例如,当 \(s = \{\texttt{b},\ \texttt{ab}\}\) 时,\(\tt ab\) 会向 \(\tt b\) 连边,因为 \(\tt ab\) 最长的(也是唯一的)在 \(s_i\) 中作为前缀出现的后缀为 \(\tt b\)。
- 再例如,当 \(s = \{\texttt{aba},\ \texttt {baba}\}\) 时,\(\tt ab\) 会向 \(\tt b\) 连边, \(\tt bab\) 会向 \(\tt ab\) 连边,\(\tt aba\) 会向 \(\tt ba\) 连边,而 \(\tt baba\) 会向 \(\tt aba\) 连边。对于每一条有向边 \(q \to fail_q\),后者是前者的后缀,也是 \(s_i\) 的前缀。
考虑用类似 KMP 的算法求解失配指针:首先令 \(fail_q\gets fail_{fa_q}\)。若当前的 \(fail_q\) 没有 \(fa_q\to q\) 这条(字典树上的)边所表示的字符 \(c\) 的转移,则令 \(fail_q\gets fail_{fail_q}\),否则 \(fail_q = \mathrm{trans}(fail_q, c)\),即字典树上在 \(fail_q\) 处添加字符 \(c\) 后到达的状态。若 \(fail_q\) 已经指向根,但还是没找到出边,则 \(fail_q\) 最终就指向根。
失配指针已经足够强大,但这并不是 AC 自动机的完全体。我们尝试将每个状态的所有字符转移 \(\delta(i, c)\) 都封闭在状态集合 \(Q\) 里面。把 KMP 自动机的转移拎出来观察
\begin{cases}
i+1 & s_{i + 1} = c \\
0 & s_{i + 1} \neq c \land i = 0 \\
\delta(nxt_i, c) & s_{i + 1} \neq c \land i \neq 0 \\
\end{cases}
\]
设字典树的根为节点 \(0\),AC 自动机的转移可类似地写为:
\mathrm{trans}(i, c) & \mathrm{if}\ \mathrm{trans}(i, c)\ \mathrm{exist} \\
0 & \mathrm{if}\ \mathrm{trans}(i, c)\ \mathrm{doesn't\ exist} \land i = 0\ (\mathrm{which\ is \ root}) \\
\delta(fail_i, c) & \mathrm{if}\ \mathrm{trans}(i, c)\ \mathrm{doesn't\ exist} \land i \neq 0
\end{cases}
\]
\(\delta(i,c)\) 表示往状态 \(i\) 后面添加字符 \(c\),所得字符串的 最长的 与 \(s_i\) 前缀 匹配的 后缀 所表示的状态。也可理解为从 \(i\) 开始跳 \(fail\) 指针,遇到的第一个有字符 \(c\) 的转移对应转移到的节点:若 \(i\) 本身有转移,则 \(\delta(i, c)\) 就等于 \(\mathrm{trans}(i, c)\),否则向上跳一层 \(fail\) 指针,等于 \(\delta(fail_i, c)\)。
根据已有信息递推,这是 动态规划 的核心思想。即求解 \(\delta\) 函数的的过程本质上是一类 DP。
当 \(\mathrm{trans}(i, c)\) 存在时,设其为 \(q\), 则有 \(fail_q = \delta(fail_i, c)\)。因为根据求 \(fail_q\) 的方法,我们会先令 \(fail_q \gets fail_i\),然后跳到第一个有字符 \(c\) 的位置,令 \(fail_q\) 等于该位置添加 \(c\) 转移到的状态。这和 \(\delta(fail_i, c)\) 的定义等价。
有了这一性质,我们就不需要预先求出失配指针,而是在建造 AC 自动机的同时一并求出。由于我们需要保证在计算一个状态的转移时,其失配指针指向的状态的转移已经计算完毕,又因为失配指针长度小于原串长度,故使用 BFS 建立 AC 自动机。一般形式的 AC 自动机代码如下:
int node, son[N][S], fa[N];
void ins(string s) { // 建出 trie 树
int p = 0;
for(char it : s) {
if(!son[p][it - 'a']) son[p][it - 'a'] = ++node;
p = son[p][it - 'a'];
}
}
void build() { // 建出 AC 自动机
queue <int> q;
for(int i = 0; i < S; i++) if(son[0][i]) q.push(son[0][i]); // 对于第一层特判,因为 fa[0] = 0,此处即转移的第二种情况
while(!q.empty()) { // 求得的 son[t][i] 就是文章中的转移函数 delta(t, i),相当于合并了 trie 和 AC 自动机的转移函数
int t = q.front(); q.pop();
for(int i = 0; i < S; i++)
if(son[t][i]) fa[son[t][i]] = son[fa[t]][i], q.push(son[t][i]); // 转移的第一种情况:原 trie 图有 trans(t, i) 的转移
else son[t][i] = son[fa[t]][i]; // 转移的第三种情况
}
}
特别的,在 ACAM 上会有一些 终止节点 \(p\),代表一个单词或以一个单词结尾,即 \(p\) 对应的字符串 \(t_p\) 的某个 后缀 在字典 \(s\) 中作为 单词 出现。 若状态 \(p\) 本身表示一个单词,即 \(t_p\in s\),则称为 单词节点。所有终止节点 \(p\) 对应着 DFA 的 接受状态集合 \(F\):ACAM 接受且仅接受以给定词典中的某一个单词结尾的字符串。
总结一下我们使用到的约定和定义:
- 节点也被称为 状态。
- 设字典树上状态 \(i\) 所表示的字符串为 \(t_i\)。
- 失配指针 \(fail_q\) 的含义为 \(q\) 所表示字符串 \(t_q\) 的最长真后缀 \(t_q[j, |t_q|]\ (2\leq j\leq |t_q| + 1)\) 使得该后缀作为某个单词的前缀出现。
- \(\delta(i,c)\) 表示往状态 \(i\) 后添加字符 \(c\),所得字符串的 最长的 与某个单词的 前缀 匹配的 后缀 所表示的状态。它也是从 \(i\) 开始,不断跳失配指针直到遇到一个有字符 \(c\) 转移的状态 \(p\),添加字符 \(c\) 后得到的状态 \(\mathrm{trans}(p, c)\)。
- 终止节点 \(p\) 代表一个单词,或以一个单词结尾。
- 所有终止节点 \(p\) 组成的集合对应着 DFA 的 接受状态集合 \(F\)。
- 若状态 \(p\) 本身表示一个单词,即 \(t_p\in s\),则称为 单词节点。
1.2 fail 树的性质与应用
AC 自动机的核心就在于 fail 树。它有非常好的性质,能够帮我们解决很多问题。
- 性质 0:它是一棵 有根树,支持树剖,时间戳拍平,求 LCA 等各种树上路径或子树操作。
- 性质 1:对于节点 \(p\) 及其对应字符串 \(t_p\),对于其子树内部所有节点 \(q\in \mathrm{subtree}(p)\),都有 \(t_p\) 是 \(t_q\) 的后缀,且 \(t_p\) 是 \(t_q\) 的后缀 当且仅当 \(q\in \mathrm{subtree}(p)\)。根据失配指针的定义易证。
- 性质 2:若 \(p\) 是终止节点,则 \(p\) 的子树全部都是终止节点。根据 fail 指针的定义,容易发现对于在 fail 树上具有祖先 - 后代关系的点对 \(p,q\),\(t_p\) 是 \(t_q\) 的 Border,这意味着 \(t_p\) 是 \(t_q\) 的后缀。因此,若 \(t_p\) 以某个单词结尾,则 \(t_q\) 也一定以该单词结尾,得证。
- 性质 3:定义 \(ed_p\) 表示作为 \(t_p\) 后缀的单词数量。若单词互不相同,则 \(ed_p\) 等于 fail 树从 \(p\) 到根节点上单词节点的数量。若单词可以重复,则 \(ed_p\) 等于这些单词节点所对应的单词的出现次数之和。
- 常用结论:一个单词在匹配串 \(S\) 中出现次数之和,等于它在 \(S\) 的 所有前缀中作为后缀出现 的次数之和。
根据性质 3,有这样一类问题:单词有带修权值,多次询问对于某个给定的字符串 \(S\),所有单词的权值乘以其在 \(S\) 中出现次数之和。根据常用结论,问题初步转化为 fail 树上带修点权,并对于 \(S\) 的每个前缀,查询该前缀所表示的状态到根的权值之和。
通常带修链求和要用到树剖,但查询具有特殊性质:一个端点是根。因此,与其单点修改链求和,不如 子树修改单点查询。实时维护每个节点的答案,这样修改一个点相当于更新子树,而查询时只需查单点。转化之前的问题需要树剖 + 数据结构 \(\log ^ 2\) 维护,但转化后即可时间戳拍平 + 树状数组单 \(\log\) 小常数解决。
补充:对于普通的链求和,只需差分转化为三个到根链求和也可以使用上述技巧。链加,单点查询 也可以通过转化变成 单点加,子树求和。只要包含一个单点操作,一个链操作,均可以将链操作转化为子树操作,即可将时间复杂度更大的树剖 BIT 换成普通 BIT。
- 性质 4:把字符串 \(t\) 放在字典 \(s\) 的 AC 自动机上跑,得到的状态为 \(t\) 的最长后缀,满足它是 \(s\) 的前缀。
1.3 应用
大部分时候,我们借助 ACAM 刻画多模式串的匹配关系,求出文本串与字典的 最长匹配后缀。但 ACAM 也可以和动态规划结合:在利用动态规划思想构建的自动机上进行 DP,这是 DP 自动机 算法。
1.3.1 结合动态规划
ACAM 除了能够进行字符串匹配,还常与动态规划相结合,因为它精确刻画了文本串与 所有 模式串的匹配情况。同时,\(\delta\) 函数自然地为动态规划的转移指明了方向。因此,当遇到形如 “不能出现若干单词” 的字符串 计数或最优化 问题,可以考虑在 ACAM 上 DP,将 ACAM 的状态写进 DP 的一个维度。
例如非常经典的 [JSOI2007]文本生成器。题目要求至少包含一个单词,补集转化相当于求 不包含任何一个单词 的长为 \(m\) 的字符串数量。考虑到我们只关心当前字符串的长度,和它与所有单词的匹配情况,设 \(f_{i,j}\) 表示长为 \(i\) 且放到所有单词建出的 ACAM 上能够转移到状态 \(j\) 的字符串数量。转移即枚举下一个字符 \(c\) 是什么,\(f_{i,j}\to f_{i+1,\delta(j,c)}\)。根据限制,需要保证 \(j\) 和 \(\delta(j,c)\) 都不是终止节点,最终答案即 \(26^m-\sum_{\\ q\in Q\land q\notin F} f_{m, q}\)。时间复杂度 \(\mathcal{O}(nm|\Sigma||s_i|)\)。
1.3.2 结合矩阵快速幂
在上一部分的基础上,若 \(\sum |s_i|\) 很小而转移轮数非常多,可以将转移写成矩阵的形式。\(\delta(p, c)\) 为我们提供了转移矩阵:添加一个字符后,从状态 \(p\) 转移到 \(q\) 的方案数为 \(\sum_\limits{c} [\delta(p, c) = q]\),即 \(A_{i, j} = \sum_\limits c [\delta(i, c) = j]\)。
具体转移方式视题目而定。矩阵乘法也可以是广义矩阵乘法,如例 XII.
1.4 注意点
- 建出字典树后不要忘记调用
build建出 ACAM。 - 注意模式串是否可以重复。
- 在构建 ACAM 的过程中,不要忘记递推每个节点需要的信息。如 \(ed_p\) 由 \(ed_{fa_p}\) 和状态 \(p\) 所表示的单词数量相加得到。
1.5 例题
I. P3808 【模板】AC 自动机(简单版)
本题相同编号的串多次出现仅算一次,因此题目相当于求:文本串 \(t\) 在模式串 \(s_i\) 建出的 ACAM 上匹配时经过的所有节点到根的路径的并上单词节点的个数。
设当前状态为 \(p\),每次跳 \(p\) 的失配指针,加上经过节点表示的单词个数(单词可能相同)并标记,直到遇到标记节点 \(q\),说明 \(q\) 到根都已经被考虑到。注意上述过程并不改变 \(p\) 本身。时间复杂度线性。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
const int S = 26;
int n, node, son[N][S], fa[N], ed[N];
string s;
void ins(string s) {
int p = 0;
for(char it : s) {
if(!son[p][it - 'a']) son[p][it - 'a'] = ++node;
p = son[p][it - 'a'];
} ed[p]++;
}
void build() {
queue <int> q;
for(int i = 0; i < S; i++) if(son[0][i]) q.push(son[0][i]);
while(!q.empty()) {
int t = q.front(); q.pop();
for(int i = 0; i < S; i++)
if(son[t][i]) fa[son[t][i]] = son[fa[t]][i], q.push(son[t][i]);
else son[t][i] = son[fa[t]][i];
}
}
int main() {
cin >> n;
for(int i = 1; i <= n; i++) cin >> s, ins(s);
int p = 0, ans = 0; cin >> s, build();
for(char it : s) {
int tmp = p = son[p][it - 'a'];
while(ed[tmp] != -1) ans += ed[tmp], ed[tmp] = -1, tmp = fa[tmp];
} cout << ans << endl;
return 0;
}
II. P2292 [HNOI2004] L 语言
首先我们有个显然的 DP:设 \(f_i\) 表示 \(i\) 前缀能否理解,那么若 存在 \(f_j = 1 \land t[j + 1,i]\in D\),则 \(f_i = 1\)。否则 \(f_i = 0\)。对 \(D\) 建出 ACAM,设 \(t[1,i]\) 跳到了状态 \(p\),我们只需要知道 \(p\) 的哪些长度的后缀是单词,这样就可以 \(\mathcal{O}(|t||s|)\) 回答单次询问,但不够快。
注意到 \(|s|\leq 20\),因此考虑状压,设 \(msk_p\):若 \(p\) 的长度为 \(l\) 的后缀是单词,则 \(msk_p\) 第 \(l\) 位为 \(1\)。这样,再用 \(S\) 记录 \(f_{i - 20}\sim f_{i - 1}\) 的状态,就可以通过位运算快速得到当前 \(f_i\) 的结果,并更新 \(S\)。
时间复杂度 \(\mathcal{O}(n|s||\Sigma| + m|t|)\),其中 \(|\Sigma|\) 表示字符集大小。
*III. P2414 [NOI2011] 阿狸的打字机
由于删去一个字符和添加一个字符对字典树大小的影响均为 \(1\),因此尽管单词长度之和可能很大,但建出的字典树大小仅有 \(m\)。设第 \(i\) 个单词在 trie 上的节点为 \(f_i\),根据应用 1,求 \(x\) 在 \(y\) 中的出现次数可以在 \(y\) 到根的每个节点上打标记,查询 \(x\) 的子树内有标记的节点个数。
因此将询问离线,按 \(y\) 从小到大的顺序处理询问(为保证修改标记的总次数线性),套上 BIT 即可。时间复杂度线性对数。代码。
IV. P5357 【模板】AC 自动机(二次加强版)
根据 fail 树的性质 1,文本串 \(S\) 在 AC 自动机上每经过一个节点就将其权值增加 \(1\),则每个单词 \(T_i\) 在 \(S\) 中的出现次数即 \(T_i\) 在 fail 树上的子树节点权值和。时间复杂度线性对数。
*V. P4052 [JSOI2007]文本生成器
ACAM 与 DP 相结合的例题。
VI. P3041 [USACO12JAN]Video Game G
非常套路的 ACAM 上 DP:设 \(f_{i, j}\) 表示长度为 \(i\) 且在 ACAM 上转移到状态 \(j\) 的字符串的最大权值,有转移 \(f_{i, j} + ed_{\delta(j, c)} \to f_{i + 1,\delta(j, c)}\)。时间复杂度 \(\mathcal{O}(nk|s_i||\Sigma|)\)。
*VII. CF1202E You Are Given Some Strings...
还算有趣的一道题目。对于同时与两个字符串相关的问题,考虑 在拼接处计算贡献,即求出 \(f_i\) 表示有多少单词是 \(t[1, i]\) 的后缀,\(g_i\) 表示有多少单词是 \(t[i, n]\) 的前缀。\(f_i\) 和 \(g_i\) 都可以用 ACAM 求出。最终答案为 \(\sum\limits_{i = 2} ^ {|t|} f_{i - 1} g_i\),时间复杂度线性。代码。
VIII. CF163E e-Government
裸题。对 \(s\) 建出 ACAM,根据应用 1,使用性质 3 部分所给出的技巧:单点修改链上求和转化为子树修改单点求和(前提是一个端点为树根),BIT 维护即可。时间复杂度线性对数。代码。
*IX. P7456 [CERC2018] The ABCD Murderer
由于单词可以重叠(否则就不可做了),我们只需求出对于每个位置 \(i\),以 \(i\) 结尾的最长单词的长度 \(L_i\)。因为对于相同的出现位置,用更短的单词去代替最长单词并不会让答案更优。使用 ACAM 即可求出 \(L_i\)。
最优化问题考虑 DP:设 \(f_i\) 表示拼出 \(s[1,i]\) 的最小代价。不难得到转移 \(f_i = \min_{\\j = i - L_i} ^ {i - 1} f_j\)。特别的,若 \(L_i\) 不存在(即没有单词在 \(s\) 中以 \(i\) 为结束位置出现)则 \(f_i\) 为无穷大。若 \(f_n\) 为无穷大则无解。可以线段树解决。
如果不想写线段树,还有一种方法:从后往前 DP。这样,每个位置可以转移到的地方是固定的(\(i-L_i\sim i - 1\)),所以用小根堆维护,懒惰删除即可。时间复杂度均为线性对数。
X. P3121 [USACO15FEB]Censoring G
非常经典的 AC 自动机题目。对 \(t\) 建出 SAM 加速匹配,每次加入一个字符,用栈在线维护字符串 \(s\) 即可。时间复杂度线性。
XI. P3715 [BJOI2017]魔法咒语
二合一屑题。考虑在 ACAM 上 DP,对于前 \(50\%\) 的数据,由于 \(L\) 很小,所以可以暴力 DP,时间复杂度 \(\mathcal{O}(L \times \sum |s_i| \times \sum |t_i|)\)。对于后 \(50\%\) 的数据,由于基本词汇长度 \(\leq 2\),故直接把 \(f_i\) 和 \(f_{i - 1}\) 放到矩阵里面递推即可。时间复杂度 \(\mathcal{O}((\sum |t_i|) ^ 3\log L)\)。
XII. CF696D Legen...
非常套路地设 \(f_{i, j}\) 表示长度为 \(i\) 且 ACAM 上状态为 \(j\) 时的最大贡献,令 \(ed_i\) 表示状态 \(i\) 所有后缀对应的所有单词权值之和,即不停跳 \(\mathrm{fail}\) 到达的所有节点权值之和,一个字典树上节点的权值为其所表示的所有单词权值之和。
显然有转移:\(f_{i, j} + ed_{\delta(j, c)}\to f_{i + 1, \delta(j, c)}\),使用矩阵快速幂优化即可。时间复杂度 \(\mathcal{O}((\sum |s_i|) ^ 3\log L)\)。代码。
*XIII. P5840 [COCI2015]Divljak
由于 \(T\) 的形态会改变,所以考虑对 \(S\) 建出 ACAM。根据 fail 树的性质,问题即转化为对给定节点 \(p\ (t_p = S_x)\) 求存在多少个 \(P\in T\) 使得 \(p\) 的子树内存在 \(P\) 的每个前缀在 ACAM 上匹配到的节点。这相当于在添加 \(P\) 时,求出其依次匹配到的节点 \(q_1, q_2, \cdots, q_{|P|}\),在 fail 树上对所有 \(q_i\) 到根的 链并 上的所有节点加 \(1\)。
上述经典问题可以通过将 \(q_i\) 按 dfs 序排序后,对 \(q_1\) 到根执行链加,然后对于每个 \(q_i\ (i > 1)\),对 \(q_i\) 到 \(\mathrm{lca}(q_{i - 1}, q_i)\) 包含 \(q_i\) 的儿子执行链加。
考虑使用 1.2 提到的技巧,将链加和单点查询转化为单点修改,子树查询,此时只需对所有 \(q_i\) 加上 \(1\),所有 \(\mathrm{lca}(q_{i - 1}, q_i)\ (i > 1)\) 减去 \(1\) 即可。时间复杂度线性对数。
2. 后缀自动机 SAM
后缀自动机全称 Suffix Automaton,简称 SAM,是一类极其有用但难以真正理解的字符串后缀结构(\(10\) 级)。它是笔者一年以前学习的算法,现在进行复习并重构学习笔记,看看能不能悟到一些新的东西。
2.1 基本定义与引理
SAM 相关的定义非常多,需要牢记并充分理解它们,否则学习 SAM 会非常吃力,因为符号化的语言相较于直观的图片和实例更难以理解。
首先,我们给出 SAM 的定义:一个长为 \(n\) 的字符串 \(s\) 的 SAM 是一个接受 \(s\) 的所有 后缀 的 最小 的有限状态自动机。具体地,SAM 有 状态集合 \(Q\),每个状态是有向无环图上的一个节点。从每个状态出发有若干条或零条 转移边,每条转移边都 对应一个字符(因此,一条路径表示一个 字符串),且从一个状态出发的转移互不相同。根据 DFA 的定义,SAM 还存在 终止状态集合 \(F\),表示从初始状态 \(T\) 到任意终止状态的任意一条路径与 \(s\) 的一个 后缀 一一对应。
SAM 最重要,也是最基本的一个性质:从 \(T\) 到任意状态的所有路径与 \(s\) 的 所有 子串 一一对应。我们称状态 \(p\) 表示字符串 \(t_p\),当且仅当存在一条 \(T\to p\) 的路径使得该路径所表示的字符串为 \(t_p\)。根据上述性质,\(t_p\) 是 \(s\) 的子串。
- 定义转移边 \(p\to q\) 表示的字符为 \(c_{p, q}\)。
- 定义 \(\delta(p, c)\) 表示状态 \(p\) 添加字符 \(c\) 转移到的状态。
- 定义 前缀 状态集合 \(P\) 由所有前缀 \(s[1, i]\) 对应的状态组成。
- SAM 的有向无环转移图也是有向无环单词图(DAWG, Directed Acyclic Word Graph)。
- \(\mathrm{endpos}(t)\):字符串 \(t\) 在 \(s\) 中所有出现的 结束位置 的 集合。例如,当 \(s = \texttt{"abcab"}\) 时,\(\mathrm{endpos}(\texttt{"ab"}) = \{2, 5\}\),因为 \(s[1 : 2] = s[4 : 5] = \texttt{"ab"}\)。
- \(\mathrm{substr}(p)\):状态 \(p\) 所表示的所有子串的 集合。
- \(\mathrm{shortest}(p)\):状态 \(p\) 所表示的所有子串中,长度 最短 的那一个子串。
- \(\mathrm{longest}(p)\):状态 \(p\) 所表示的所有子串中,长度 最长 的那一个子串。
- \(\mathrm{minlen}(p)\):状态 \(p\) 所表示的所有子串中,长度 最短 的那一个子串的 长度。\(\mathrm{minlen}(i) = |\mathrm{shortest}(i)|\)。
- \(\mathrm{len}(i)\):状态 \(p\) 所表示的所有子串中,长度 最长 的那一个子串的 长度。\(\mathrm{len}(i)=|\mathrm{longest}(i)|\)。
两个字符串 \(t_1, t_2\) 的 \(\mathrm{endpos}\) 可能相等。例如当 \(s = \texttt{"abab"}\) 时,\(\mathrm{endpos}(\texttt{"b"}) = \mathrm{endpos}(\texttt{"ab"})\)。这样,我们可以将 \(s\) 的子串划分为若干 等价类,用一个状态表示。SAM 的每个状态对应若干 \(\mathrm{endpos}\) 集合相同的子串。换句话说,\(\forall t\in \mathrm{substr}(p)\),\(\mathrm{endpos}(t)\) 相等。因此,SAM 的状态数等于所有子串的等价类个数(初始状态对应空串)。
读者应该有这样的直观印象:SAM 的每个状态 \(p\) 都表示一个独一无二的 \(\mathrm{endpos}\) 等价类,它对应着在 \(s\) 中出现位置相同的一些子串 \(\mathrm{substr}(p)\)。\(\mathrm{shortest}(p),\mathrm{longest}(p),\mathrm{minlen}(p)\) 和 \(\mathrm{len}(p)\) 描述了 \(\mathrm{substr}(p)\) 最短和最长的子串及其长度。
转移边与 \(\mathrm{substr}\) 的联系:任意一条 \(T\to p\) 的路径 \(P\) 所表示的字符串 \(t_{P}\in \mathrm{substr}(p)\)。
在引出 SAM 的核心定义「后缀链接」前,我们需要证明关于上述概念的一些性质。下列引理的内容部分来自 OI-wiki,相关链接见 Part 2.4.
引理 1:考虑两个非空子串 \(u\) 和 \(w\)(假设 \(|u|\leq |w|\))。要么 \(\mathrm{endpos}(u)\cup \mathrm{endpos}(w)=\varnothing\),要么 \(\mathrm{endpos}(w) \subseteq \mathrm{endpos}(u)\),取决于 \(u\) 是否为 \(w\) 的一个后缀:
\[\begin{cases}
\mathrm{endpos}(w) \subseteq \mathrm{endpos}(u) & \mathrm{if} \ u\ \mathrm{is\ a\ suffix\ of}\ w \\
\mathrm{endpos}(u) \cup \mathrm{endpos}(w) = \varnothing & \mathrm{otherwise}
\end{cases}
\]
证明:若存在位置 \(i\) 满足 \(i\in \mathrm{endpos}(u)\) 且 \(i\in \mathrm{endpos}(w)\),说明 \(u\) 和 \(w\) 以 \(i\) 为结束位置在 \(s\) 中出现。由于 \(|u|\leq |w|\),所以 \(u\) 必然是 \(w\) 的后缀,因此 \(w\) 出现的位置 \(u\) 必然以 \(w\) 的后缀形式出现,即对于任意 \(i\in \mathrm{endpos}(w)\) 有 \(i\in \mathrm{endpos}(u)\)。否则不存在这样的位置 \(i\),即 \(\mathrm{endpos}(u) \cup \mathrm{endpos}(w) = \varnothing\)。
引理 2:考虑一个状态 \(p\)。\(p\) 所表示的所有子串长度连续,且 较短者总是较长者的后缀。
证明:根据引理 1,若两个子串 \(\mathrm{endpos}\) 相同(这也说明它们属于相同状态),则较短者总是较长者的后缀,后半部分得证。
对于前半部分考虑反证:假设 \(\mathrm{longest}(p)\) 长为 \(L\ (\mathrm{minlen}(p) < L < \mathrm{len}(p))\) 的后缀 \(t_L\notin \mathrm{substr}(p)\)。由于 \(t_L\) 是 \(\mathrm{longest}(p)\) 的 真后缀,故 \(\mathrm{endpos}(\mathrm{longest}(p)) \subseteq \mathrm{endpos}(t_L)\)。根据假设,\(\mathrm{endpos}(\mathrm{longest}(p)) \neq \mathrm{endpos}(t_L)\)。又因为 \(\mathrm{shortest}(p)\) 是 \(t_L\) 的 真后缀,故 \(\mathrm{endpos}(t_L) \subseteq \mathrm{endpos}(\mathrm{shortest}(p))\),因此 \(|\mathrm{endpos}(\mathrm{longest}(p))| < |\mathrm{endpos}(t_L)| \leq |\mathrm{endpos}(\mathrm{shortest}(p))|\),这与 \(\mathrm{endpos}(\mathrm{longest}(p)) = \mathrm{endpos}(\mathrm{shortest}(p))\) 矛盾,证毕。
简单地说,对于一个子串 \(t\) 的所有后缀,其 \(\mathrm{endpos}\) 集合大小随着后缀长度减小而单调不降。这很好理解:后缀越长,在 \(s\) 中出现的位置就越少。
推论 1:对于子串 \(t\) 的所有后缀,其 \(\mathrm{endpos}\) 集合大小随后缀长度减小而单调不降,且 较小的 \(\mathrm{endpos}\) 集合包含于较大的 \(\mathrm{endpos}\) 集合。
引理 2 是非常重要的性质。有了它,我们就可以定义后缀链接了。
- 定义状态 \(p\) 的 后缀链接 \(\mathrm{link}(p)\) 指向 \(\mathrm{longest}(p)\) 最长 的一个后缀 \(w\) 满足 \(w\notin \mathrm{substr}(p)\) 所在的状态。换句话说,一个后缀链接 \(\mathrm{link}(p)\) 连接到对应于 \(\mathrm{longest}(p)\) 最长的处于另一个 \(\mathrm{endpos}\) 等价类的后缀所在的状态。根据引理 2,\(\mathrm{minlen}(i) = \mathrm{len(link}(i))+1\)。
引理 3:所有后缀链接形成一棵以 \(T\) 为根的树。
证明:对于任意不等于 \(T\) 的状态,沿着后缀链接移动总能达到一个所表示字符串更短的状态,直到 \(T\)。
- 定义 后缀路径 \(p\to q\) 表示在后缀链接形成的树上 \(p\to q\) 的路径。
引理 4:通过 \(\mathrm{endpos}\) 集合构造的树(每个子节点的 \(\mathrm {subset}\) 都包含在父节点的 \(\mathrm{subset}\) 中)与通过后缀链接 \(\mathrm{link}\) 构造的树相同。
根据推论 1 与后缀链接的定义容易证明。因此,后缀链接构成的树本质上是 \(\mathrm{endpos}\) 集合构成的一棵树。
上图图源 OI-wiki。我们给出每个状态的 \(\mathrm{endpos}\) 集合以便更好理解引理 4:\(\mathrm{endpos}(\texttt{"a"}) = \{1\}\),
\mathrm{endpos}(\texttt{"ab"}) = \{2\} \\
\mathrm{endpos}(\texttt{"abcb", "bcb", "cb"}) = \{4\} \\
\end{aligned}
\subsetneq
\mathrm{endpos}(\texttt{"b"}) = \{2, 4\} \\
\]
\mathrm{endpos}(\texttt{"abc"}) = \{3\} \\
\mathrm{endpos}(\texttt{"abcbc", "bcbc", "cbc"}) = \{5\} \\
\end{aligned}
\subsetneq
\mathrm{endpos}(\texttt{"bc", "c"}) = \{3, 5\} \\
\]
2.2 关键结论
我们还需要以下定理确保构建 SAM 的算法的正确性,并使读者对上述定义形成感性的直观的认知。
结论 1.1:从任意状态 \(p\) 出发跳后缀链接到 \(T\) 的路径,所有状态 \(q\in p\to T\) 的 \([\mathrm{minlen}(q),\mathrm{len}(q)]\) 不交,单调递减且并集形成 连续 区间 \([0,\mathrm{len}(p)]\)。
证明:根据后缀链接的性质 \(\mathrm{len}(\mathrm{link}(p)) + 1 = \mathrm{minlen}(p)\) 即证。
结论 1.2:从任意状态 \(p\) 出发跳后缀链接到 \(T\) 的路径,所有状态 \(q\in p\to T\) 的 \(\mathrm{substr}(q)\) 的并集为 \(\mathrm{longest}(p)\) 的 所有后缀。
证明:由结论 1.1 和后缀链接的定义易证。
结论 2.1:\(\forall t_p\in \mathrm{substr}(p)\),若存在 \(p\to q\) 的 转移边,则 \(t_p + c_{p,q}\in \mathrm{substr}(q)\)。
证明:根据 \(\mathrm{substr}\) 的定义可得。
结论 2.2:\(\forall t_q\in \mathrm{substr}(q)\),若存在 \(p\to q\) 的转移边,则 \(\exist t_p\in \mathrm{substr}(p)\) 使得 \(t_p+c_{p,q} = t_q\)。
证明:结论 2.1 的逆命题。这很好理解,因为对于任意 \(t_q\in \mathrm{substr}(q)\),若不存在这样的 \(t_p + c_{p,q} = t_q\),那么就不存在 \(T\to q\) 的路径使得其所表示字符串为 \(t_p + c_{p,q}\),这与 \(t_q\in \mathrm{substr}(q)\) 矛盾。
结论 3.1:考虑状态 \(q\),不存在转移 \(p\to q\) 使得 \(\mathrm{len}(p) + 1 > \mathrm{len}(q)\)。
证明:显然。
结论 3.2:考虑状态 \(q\),**唯一 **存在状态 \(p\) 和转移 \(p\to q\) 使得 \(\mathrm{len}(p) + 1 = \mathrm{len}(q)\)。
证明:考虑反证法,若不存在这样的 \(p\),说明 \(\forall p,\mathrm{len}(p)+1<\mathrm{len}(q)\)。根据结论 2.2,\(\mathrm{substr}(q)\) 中最长的一个串的长度为 \(\max_{\\ t_p\in \mathrm{substr}(p)} |t_p| + 1\) 即 \(\max_{\\ p} \mathrm{len}(p) + 1\)。根据 \(\mathrm{len}\) 的定义与 \(\mathrm{len}(p) + 1 < \mathrm{len}(q)\),推得 \(\mathrm{len}(q) < \mathrm{len}(q)\),矛盾。唯一性不难证明。
简单地说,若数集 \(T\) 由若干数集 \(S\) 的并加上 \(1\) 后得到,那么 \(\max_{\\ s\in S}s + 1 = \max_{\\ t\in T}t\)。
结论 3.3:考虑状态 \(q\),唯一 存在转移 \(p\to q\) 使得 \(\mathrm{minlen}(p) + 1 = \mathrm{minlen}(q)\)。
证明:同理。
- 定义 \(\mathrm{maxtrans}(q)\) 表示使得 \(\mathrm{len}(p) + 1 = \mathrm{len}(q)\) 且存在转移 \(p\to q\) 的唯一的 \(p\)。
- 定义 \(\mathrm{mintrans}(q)\) 表示使得 \(\mathrm{minlen}(p) + 1 = \mathrm{minlen}(q)\) 且存在转移 \(p\to q\) 的唯一的 \(p\)。
结论 4.1:考虑状态 \(q\),若存在转移 \(p\to q\),则 \(p\) 在后缀链接树上是 \(\mathrm{maxtrans}(q)\) 或其祖先。
证明:由于所有 \(p\) 转移到相同状态 \(q\),故所有 \(p\) 的 \(\mathrm{substr}(p)\) 的并,短串为长串的后缀。根据 \(\mathrm{link}\) 树的性质即证。
结论 4.2:考虑状态 \(q\),若存在转移 \(p\to q\),则 \(p\) 在后缀链接树上是 \(\mathrm{mintrans}(q)\) 或其子节点。
证明:同理。
结论 4.3:考虑状态 \(q\),若存在转移 \(p\to q\),则所有这样的 \(p\) 在 \(\mathrm{link}\) 树上形成了一条 深度递减的链 \(\mathrm{maxtrans}(q)\to \mathrm{mintrans}(q)\)。
证明:结合结论 4.1 与结论 4.2 易证。
可以发现上述性质大都与后缀链接有关,因为后缀链接是 SAM 所提供的最重要的核心信息。我们甚至可以抛弃 SAM 的 DAWG,仅仅使用后缀链接就可以解决大部分字符串相关问题。
- 扩展定义:\(\mathrm{substr}(p\to q)\) 表示后缀路径 \(p\to q\) 上所有状态的 \(\mathrm{substr}\) 的并。
2.3 构建 SAM
铺垫了这么多,我们终于有足够的性质来建造 SAM 了。之前的长篇大论可能让读者认为它是一个非常复杂的算法:是,但不完全是。至少在代码实现方面,它比同级的 LCT 简单到不知道到哪里去了。
SAM 的构建核心思想是 增量法。我们在 \(s[1,i-1]\) 的 SAM \(A_{i - 1}\) 的基础上进行更新,从而得到 \(s[1,i]\) 的 SAM \(A_i\)。因此,该算法是 在线 算法。它主要分为三个步骤:
- 打开 SAM。
- 把字符插进去。
- 关上 SAM。
设 \(s[1,i - 1]\) 在 \(A_{i - 1}\) 上的状态为 \(las\),当前状态数量为 \(cnt\)。\(las\) 和 \(cnt\) 的初始值均为 \(1\),表示初始状态 \(T = 1\)。不要忘记初始化 \(las\) 和 \(cnt\)。
新建初始状态 \(cur \gets cnt + 1\),并令 \(cnt\) 自增 \(1\) 表示状态数量增加 \(1\)。\(cur\) 即 \(s[1,i]\) 在 \(A_i\) 上对应的状态。\(\mathrm{endpos}(cur) = \{i\}\)。令变量 \(p\gets las\) 防止接下来的操作改变 \(las\)。
接下来我们考虑如何连指向 \(cur\) 的转移边:由于 \(las\to T\) 的后缀路径上的所有状态表示了所有 \(s[1, i - 1]\) 的后缀,因此若 \(p\) 没有 \(s_i\) 的转移边,就新建 \(p\to cur\) 字符为 \(s_i\) 的转移,并令 \(p\gets \mathrm{link}(p)\) 表示跳后缀链接。直到遇到路径上第一个有 \(s_i\) 出边的状态 \(p\),此时就应该 停止 了,因为再连下去 \(T\to p\to \delta(p, s_i)\) 和 \(T\to p\to cur\) 会表示相同字符串,使相同出边指向两个不同节点,与 SAM 的性质相违背。此时需要分三种情况讨论:
Case 1:不存在 \(p\)。即后缀路径 \(las\to T\) 上的所有状态都没有字符 \(s_i\) 的转移边。
容易发现这种情况仅在 \(s_i\) 未在 \(s[1:i-1]\) 中出现过时发生。我们只需令 \(\mathrm{link}(cur)\gets T\) 即可。
Case 2:存在 \(p\),令 \(q = \delta(p,s_i)\) 且 \(\mathrm{len}(p) + 1 = \mathrm{len}(q)\)。
令 \(\mathrm{link}(cur)\gets q\) 即可,原因如下:设 \(las\to T\) 后缀路径上 \(p\) 的前一个状态为 \(p'\)。根据操作,可知 \(p'\to cur\) 有一条转移边。则此时 \(\mathrm{minlen}(cur) = \mathrm{minlen}(p') + 1 = (\mathrm{len}(p) + 1) + 1 = \mathrm{len}(q) + 1\),说明 \(q\) 恰好与 \(cur\) 的后缀链接的定义相匹配。
可以证明 \(\mathrm{substr}(q\to T)\) 是 \(s[1,i]\) 所有长度 \(\leq \mathrm{len}(q)\) 的后缀:由于 \(\mathrm{substr}(las\to T)\) 是 \(s[1,i - 1]\) 的所有后缀,又因为 \(p\) 在 \(las\to T\) 上,所以 \(\mathrm{longest}(p)\) 是 \(s[1,i-1]\) 长为 \(\mathrm{len}(p)\) 的后缀。而 \(p\to q\) 存在字符为 \(s_i\) 的转移边,故 \(\mathrm{longest}(q)\) 是 \(s[1,i]\) 长为 \(\mathrm{len}(p) + 1=\mathrm{len}(q)\) 的后缀。再根据结论 1.2 得证。这同时也证明了 \(\mathrm{link}(cur)\gets q\) 这一操作的正确性。
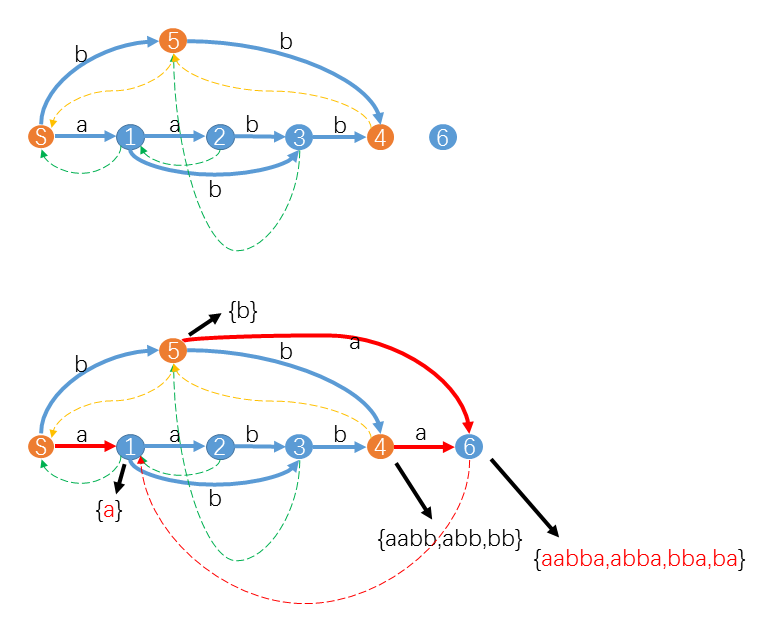
图源 hihocoder。上图中,在插入 \(s_5 = \texttt{a}\) 时,状态 \(p=las = 4\) 没有字符 \(\tt a\) 的转移,因此令 \(\delta(4,\texttt a ) = cur = 6\),然后 \(p\gets \mathrm{link}(p) = 5\)。状态 \(5\) 也没有字符 \(\tt a\) 的转移,因此令 \(\delta(5,\texttt a ) = 6\),然后 \(p\gets \mathrm{link}(p)= T\),也就是图中的 \(S\)。
\(\delta(T,\texttt a )\) 存在,此时 \(p = T, q = \delta(T,\texttt a ) = 1\)。因为 \(\mathrm{len}(T) + 1 = \mathrm{len}(1)\),所以令 \(\mathrm{link}(6)\gets 1\) 即可。
注意状态 \(4,5,6\) 所表示的子串,可以发现 \((\mathrm{substr}(4)\cup \mathrm{substr}(5)) + \texttt{a} = \mathrm{substr}(6)\)。这很好地验证了结论 2.1 和结论 2.2。
Case 3:存在 \(p\),令 \(q = \delta(p,s_i)\) 但 \(\mathrm{len}(p) + 1 \neq \mathrm{len}(q)\)。
此时 \(\mathrm{len}(p) + 1 < \mathrm{len}(q)\),我们需要将 \(q\) 拆成两个状态 \(q_1\) 和 \(q_2\),将 \(\mathrm{substr}(q)\) 分成长度小于等于 \(\mathrm{len}(p) + 1\) 和大于 \(\mathrm{len}(p) + 1\) 两部分。具体地,先令 \(cnt \gets cnt + 1\),然后新建一个状态 \(cl \gets cnt\) 表示将 \(\mathrm{substr}(q)\) 长度 \(\leq \mathrm{len}(p) + 1\) 的部分丢给 \(cl\):
- \(\mathrm{minlen}(cl)\) 等于原来的 \(\mathrm{minlen}(q)\)。
- \(\mathrm{len}(cl)\) 等于 \(\mathrm{len}(p) + 1\)。
- 新的 \(\mathrm{minlen}(q)\) 等于 \(\mathrm{len}(cl) + 1\)。
考虑 \(cl\) 如何继承 \(q\) 这一状态:首先,\(q\) 的所有转移要原封不动地存下来,故对于每个字符 \(c\) 都要 \(\delta(cl, c) \gets \delta(q, c)\)。此外,由于 \(\mathrm{minlen}(cl)\) 等于原来的 \(\mathrm{minlen}(q)\),因此 \(\mathrm{link}(cl) \gets\) 原来的 \(\mathrm{link}(q)\)。同时,新的 \(\mathrm{minlen}(q)\) 等于 \(\mathrm{len}(cl) + 1\) 也即 \(\mathrm{len}(p) + 1\),所以 \(\mathrm{link}(q),\mathrm{link}(cur)\gets cl\)。
此外,根据结论 4.3,我们知道后缀路径 \(p\to T\) 上转移到 \(q\) 的状态一定是路径的一段前缀,对于前缀上的所有节点 \(p’\),我们需要把 \(\delta(p', s_i)\) 从本来的 \(q\) 改成 \(cl\),因为我们把 \(\mathrm{substr}(q)\) 长度 \(\leq \mathrm{len}(p) + 1\) 的串丢给了状态 \(cl\),所以对于原本能转移到 \(q\) 的所有 \(\mathrm{len}\) 值 \(\leq \mathrm{len}(p)\) 的状态(显然也是 \(p\to T\) 路径的前缀),都需要将字符 \(s_i\) 的转移 重定向 至 \(cl\)。
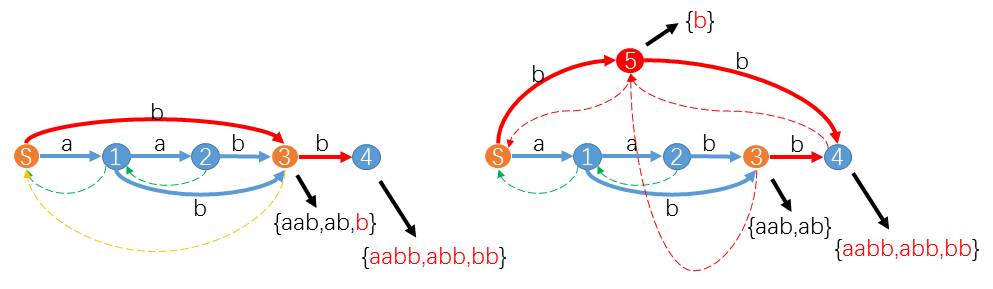
上图中,我们把 \(q = 3\) 的不大于 \(\mathrm{len}(p = T) + 1 = 1\) 的所有子串提出来,丢给一个新建的状态 \(cl=5\),然后 \(\mathrm{link}(cur = 4)\gets cl = 5\)。内部 \(\mathrm{link}(q = 3)\gets cl = 5\),同时 \(\mathrm{link}(cl = 5) \gets p = T\),即原来的 \(\mathrm{link}(q)\)。
然后,从 \(p = T\) 往上跳后缀连接直到不存在连向 \(q = 3\) 的路径或到达根节点 \(T\),表示对于 \(p\to T\) 的一段前缀,满足前缀上所有状态添加字符 \(s_i\) 能够转移到 \(q = 3\),将它们字符为 \(s_i\) 的转移重定向至 \(cl = 5\)(当然,上例只有 \(T\) 一个点,不过并不一定会跳到 \(T\),因为可能跳到中间的某个状态 \(p'\) 时就没有转移 \((p',q = 3)\) 了),即 \((T,3)\) 变为了 \((T,5)\)。
上述分类讨论结束后,令 \(las\gets cur\) 表示添加字符 \(s_{i+1}\) 时 \(s[1,i]\) 在 \(A_i\) 对应状态 \(cur\)。在实现中,我们通常在连接转移边之前执行该操作。构建 SAM 的代码如下:
const int N = 1e5 + 5;
const int S = 26;
int cnt = 1, las = 1, son[N][S], fa[N], len[N];
void ins(char s) {
int it = s - 'a', p = las, cur = ++cnt;
len[cur] = len[p] + 1, las = cur; // 计算 len[cur],更新 las
while(!son[p][it]) son[p][it] = cur, p = fa[p]; // 添加转移边
if(!p) return fa[cur] = 1, void(); // case 1
int q = son[p][it];
if(len[p] + 1 == len[q]) return fa[cur] = q, void(); // case 2
int cl = ++cnt; cpy(son[cl], son[q], S); // 新建节点,cl 继承 q 的所有转移
len[cl] = len[p] + 1, fa[cl] = fa[q], fa[q] = fa[cur] = cl; // 计算 len[cl] 以及 cl, q, cur 的后缀链接,注意 fa[cl] = fa[q] 要在 fa[q] = cl 之前
while(son[p][it] == q) son[p][it] = cl, p = fa[p]; // 修改后缀路径 p -> T 的一段前缀
}
当字符集 \(\Sigma\) 非常大的时候,时空复杂度均无法接受,因此需要使用平衡树维护每个状态的所有转移边,可以用 map 代替。
2.4 时间复杂度证明
下设字符串 \(s\) 长度为 \(n\),证明大部分摘自 OI wiki。
2.4.1 状态数上界
构建后缀自动机的算法本身就已经证明了其 SAM 状态数不超过 \(2n-1\):插入 \(s_1,s_2\) 时分别产生一个状态,后续插入每个 \(s_i\) 时最多产生两个状态,因此当 \(n>1\) 时状态数不超过 \(2n-2\),形如 \(\tt abb\cdots bb\) 的字符串达到上界。当 \(n=1\) 时状态数为 \(2n-1\)。
2.4.2 转移数上界
称 \(\mathrm{len}(p) + 1 = \mathrm{len}(q)\) 的转移 \((p, q)\) 为连续的,显然,从一个非终止状态 \(p\) 出发 有且仅有 一条连续转移 \((p,q)\),对于 \(q\) 也有且仅有一个对应的 \(p\)。因此,连续转移总数不超过 \(2n-2\)。对于不连续的转移,找到从根节点 \(T\to p\) 的一条连续路径,设其所表示字符串为 \(u\);找到从 \(q\) 到任意一个终止节点 \(f\in F\) 的一条连续路径,设其所表示字符串为 \(v\)。对于不同的 \(p,q\),\(s_{p,q} = u + c_{p,q} + v\) 互不相同:若两个转移 \((p,q)\) 和 \((p', q')\) 出现 \(s_{p, q} = s_{p', q'}\) 的情况,由于不同路径所表示字符串不同,因此 \((p, q)\) 和 \((p', q')\) 在同一条路径,这与 \(T\to p\) 和 \(q\to F\) 连续矛盾。又因为 \(s_{p, q}\) 是 \(s\) 的真后缀(\(s\) 对应的路径转移显然连续),因此不连续的转移数量不超过 \(n-1\)。这样,我们得到了转移数上界 \(3n-3\)。
由于最大的状态数量仅在形如 \(\tt abb \cdots bb\) 的字符串中达到,此时转移数量小于 \(3n - 3\)。形如 \(\tt abb\cdots bbc\) 的字符串达到了 \(3n - 4\) 的上界。
2.4.3 操作次数上界
该部分 OI Wiki 上讲得较为简略,因此笔者自行证明了这一结论。在构建 SAM 的过程中,有且仅有将 \(p\to q\) 的转移边改为 \(p\to cl\) 的操作 不新建 转移边。因此,基于 转移数线性 这一结论,其它操作的时间复杂度均为线性。
定义 \(\mathrm{depth}(p)\) 表示 \(p\) 在 \(\rm link\) 树上的 深度。引理:若 \(p\to q\) 存在转移边,则 \(\mathrm{depth}(p)\geq \mathrm{depth}(q)\)。证明:
- 考虑后缀路径 \(q\to T\) 上的任意两个不同状态 \(q_1, q_2\ (q_1 \neq q_2)\)。设 \(p_1\) 为任意能转移到 \(q_1\) 的状态,\(p_2\) 为任意能转移到 \(q_2\) 的状态。因为 \(\mathrm{substr}(q_1), \mathrm{substr}(q_2)\) 均为 \(\mathrm{longest}(q)\) 的后缀,因此 \(\mathrm{substr}(p_1), \mathrm{substr}(p_2)\) 均为 \(\mathrm{longest}(p)\) 的后缀。所以 \(p_1, p_2\) 均在后缀路径 \(p\to T\) 上。
- 若 \(p_1 = p_2\),则 \(p_1\) 通过同一字符能转移到不同状态,矛盾。因此 \(p_1\neq p_2\)。故能转移到 \(q\to T\) 上 任意 状态 \(q’\) 的所有状态 \(p'\) 均在 \(p\to T\) 上且 互不相同。由于对于每个 \(q'\) 至少存在一个与之对应的 \(p'\)(可能存在多个),因此 \(|q\to T|\leq |p\to T|\),即 \(\mathrm{depth}(p)\geq \mathrm{depth}(q)\)。证毕。
- 可结合下图以更好理解,其中 \(i \to i - 1\) 的边表示一条后缀链接,其余边表示转移边。
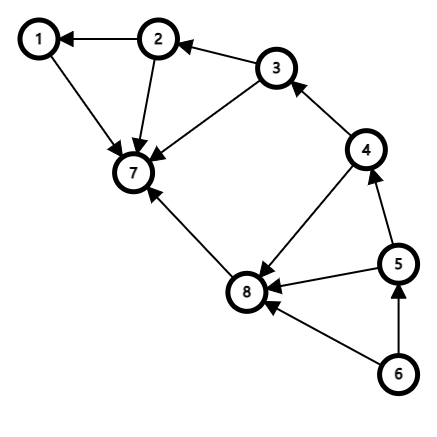
假设我们从 \(p\) 一直跳到 \(p'\),并将 \(p\to p'\) 路径上所有状态指向 \(q\) 的转移边改为指向 \(cl\)。设 \(q' = \delta(\mathrm{link}(p'), s_i)\),容易证明 原 \(\mathrm{link}(q)\) 即 现 \(\mathrm{link}(cl) = q'\)。设 \(d = \mathrm{depth}(p) - \mathrm{depth}(p')\),即从 \(p\) 开始跳 \(\mathrm{link}\) 的次数。根据上述引理,我们有 \(\mathrm{depth}(q') \leq \mathrm{depth}(p') = \mathrm{depth}(p) - d \leq \mathrm{depth}(las) - 1 - d\)。
同时,根据 \(\mathrm{link}(cur) = cl\),\(\mathrm{link}(cl) = q'\) 可知 \(\mathrm{depth}(cur) - 2 \leq \mathrm{depth}(las) - 1 - d\),即 \(d\leq \mathrm{depth}(las) - \mathrm{depth}(cur) + 1\),这一不等式通过精确分析还可以更紧。因此,该部分操作的总时间复杂度可用 \(cur\) 相对于 \(las\) 的 深度减少量之和 来估计。同时,若进入 Case 1 或 Case 2,则因为 \(las\to cur\) 存在转移边,由引理得 \(\mathrm{depth}(cur)\leq \mathrm{depth}(las)\),若进入 Case 3,则根据上述不等式有 \(\mathrm{depth}(cur) \leq \mathrm{depth}(las) + 1\)。因此,势能分析得到 \(\sum d\) 的级别为线性。
2.5 应用
2.5.1 求本质不同子串个数
根据 SAM 的性质,每个子串唯一对应一个状态,因此答案即 \(\sum \mathrm{len}(i) - \mathrm{len}(\mathrm{link}(i))\)。
2.5.2 字符串匹配
用文本串 \(t\) 在 \(s\) 的 SAM 上跑匹配时,我们可以得到对于 \(t\) 的每个 前缀 \(t[1, i]\),其作为 \(s\) 的子串出现的 最长后缀 \(L_i\):若当前状态 \(p\)(即 \(t[i - L_{i - 1}, i - 1]\) 所表示的状态)不能匹配 \(t_i\)(即 \(\delta(p, t_i)\) 不存在),就跳后缀链接令 \(p\gets \mathrm{link}(p)\) 并实时更新 \(L_i = \mathrm{len}(p)\) 直到 \(p = T\) 或 \(\delta(p, t_i)\) 存在,对于后者令 \(p\gets \delta(p, t_i)\),\(L_i\) 还需再加上 \(1\)。若能匹配,则直接令 \(p\gets \delta(p, t_i)\) 并令 \(L_i\gets L_{i - 1} + 1\)。综合一下,我们得到如下代码:
for(int i = 1, p = 1, L = 0; i <= n; i++) {
while(p > 1 && !son[p][t[i] - 'a']) L = len[p = fa[p]];
if(son[p][t[i] - 'a']) L = min(L + 1, len[p = son[p][t[i] - 'a']]);
}
2.6 广义 SAM
广义 SAM,GSAM,全称 General Suffix Automaton,相对于普通 SAM 它支持对多个字符串进行处理。它可以看做对 trie 建后缀自动机。
一般的写法是每插入一个字符串前将 \(las\) 指针置为 \(T\),非常方便。一个细节:构建单串 SAM 时,\(\delta(las, s_i)\) 一定不存在,但对于多串 SAM 可能存在。这说明当前字符串 \(s\) 的 \(i\) 前缀是某个已经添加过的字符串的子串。我们需要进行以下特判,否则会出现这种情况:https://www.luogu.com.cn/discuss/322224 。
- 当 \(q = \delta(las, s_i)\) 存在,且 \(\mathrm{len}(las) + 1 = \mathrm{len}(q)\) 时,令 \(las\gets q\) 并直接返回。
- 当 \(q = \delta(las, s_i)\) 存在,且 \(\mathrm{len}(las) + 1 \neq \mathrm{len}(q)\) 时,我们会新建节点 \(cl\),并进行复制。此时,令 \(las\gets cl\) 而非 \(cur\)。这是因为 \(\mathrm{len}(cur) = \mathrm{len}(las) + 1\) 且 \(\mathrm{len}(cl) = \mathrm{len}(las) + 1\),又因为 \(\mathrm{link}(cur) = cl\),所以这说明 \(\mathrm{substr}(cur) = \varnothing\),即 节点 \(cur\) 是空壳,真正的信息在 \(cl\) 上面。为此,我们舍弃掉这个 \(cur\),并用 \(cl\) 代替它。
int ins(int p, int it) {
if(son[p][it] && len[son[p][it]] == len[p] + 1) return son[p][it]; // 如果节点已经存在,且 len 值相对应,即 (p, son[p][it]) 是连续转移,则直接转移。
int cur = ++cnt, chk = son[p][it]; len[cur] = len[p] + 1;
while(!son[p][it]) son[p][it] = cur, p = fa[p];
if(!p) return fa[cur] = 1, cur;
int q = son[p][it];
if(len[p] + 1 == len[q]) return fa[cur] = q, cur;
int cl = ++cnt; cpy(son[cl], son[q], S);
len[cl] = len[p] + 1, fa[cl] = fa[q], fa[q] = fa[cur] = cl;
while(son[p][it] == q) son[p][it] = cl, p = fa[p];
return chk ? cl : cur; // 如果 len[las][it] 存在,则 cur 是空壳,返回 cl 即可
}
上述方法本质相当于对匹配串建出 trie 后进行 dfs 构建 SAM。部分特殊题目会直接给出 trie 而非模板串,此时模板串长度之和的级别为 \(\mathcal{O}(|S| ^ 2)\),因此只能 bfs 构建 SAM:设 \(P_p\) 表示 trie 树上状态 \(p\) 在 SAM 上对应的位置,若 trie 树 \(T\) 上的转移 \(q = \delta_T(p, c)\) 存在,其中 \(c\) 是 \(p\to q\) 所表示字符,那么以 \(P_p\) 作为 \(las\),插入字符 \(c\) 后新的 \(las\) 即 \(P_q\)。此时 不需要 像上面一样特判,因为 \(\delta(P_p, c)\) 必然不存在,这是由于 bfs 使得 \(\mathrm{len}(P_p)\) 单调不降。模板题 P6139 代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define cpy(x, y, s) memcpy(x, y, sizeof(x[0]) * (s))
const int N = 2e6 + 5;
const int S = 26;
ll n, ans, cnt = 1;
string s;
int len[N], fa[N], son[N][S];
int ins(int p, int it) {
int cur = ++cnt; len[cur] = len[p] + 1;
while(!son[p][it]) son[p][it] = cur, p = fa[p];
if(!p) return fa[cur] = 1, cur;
int q = son[p][it];
if(len[p] + 1 == len[q]) return fa[cur] = q, cur;
int cl = ++cnt; cpy(son[cl], son[q], S);
len[cl] = len[p] + 1, fa[cl] = fa[q], fa[q] = fa[cur] = cl;
while(son[p][it] == q) son[p][it] = cl, p = fa[p];
return cur;
}
int node = 1, pos[N], tr[N][S];
void ins(string s) {
int p = 1;
for(char it : s) {
if(!tr[p][it - 'a']) tr[p][it - 'a'] = ++node;
p = tr[p][it - 'a'];
}
}
void build() {
queue <int> q; q.push(pos[1] = 1);
while(!q.empty()) {
int t = q.front(); q.pop();
for(int i = 0, p; i < S; i++) if(p = tr[t][i])
pos[p] = ins(pos[t], i), q.push(p);
}
}
int main() {
cin >> n;
for(int i = 1; i <= n; i++) cin >> s, ins(s);
build();
for(int i = 2; i <= cnt; i++) ans += len[i] - len[fa[i]];
cout << ans << endl;
return 0;
}
2.7 常用技巧与结论
2.7.1 线段树合并维护 \(\mathrm{endpos}\) 集合
对于部分题目,我们需要维护每个状态的 \(\mathrm{endpos}\) 集合,以刻画每个子串在字符串中所有出现位置的信息。
为此,我们在 \(s[1, i]\) 对应状态的 \(\mathrm{endpos}\) 集合里插入位置 \(i\),再根据 \(\mathrm{endpos}\) 集合构造出来的树本质上就是后缀链接树这一事实,在 \(\mathrm{link}\) 树上进行 线段树合并 即可得到每个状态的 \(\mathrm{endpos}\) 集合。这是一个非常有用且常见的技巧。
注意,线段树合并时会破坏原有线段树的结构,因此若需要在线段树合并后保留每个状态的 \(\rm endpos\) 集合对应的线段树的结构,需要在线段树合并时 新建节点。即 可持久化线段树合并。SAM 相关问题的线段树合并通常均需要可持久化。
特别的,如果仅为了得到 \(\mathrm{endpos}\) 集合大小,那么只需求出每个状态在 \(\mathrm{link}\) 树上的子树有多少个表示 \(s\) 的前缀的状态。前缀状态即所有曾作为 \(cur\) 的节点。对此,有两种解决方法:直接建图 dfs,以及 ——
2.7.2 桶排确定 dfs 顺序
显然后缀链接树上父亲的 \(\mathrm{len}\) 值一定小于儿子,但千万不能认为编号小的节点 \(\mathrm{len}\) 值也小。因此,对所有节点按照 \(\mathrm{len}\) 值从大到小进行桶排序,然后按顺序合并每个状态及其父亲是正确的,并且常数比建图 + dfs 小不少,代码见例题 I.
2.7.3 快速定位子串
给定区间 \([l, r]\),求 \(s_{l, r}\) 在 SAM 上的对应状态:在构建 SAM 时容易预处理 \(s_{1, i}\) 所表示的状态 \(pos_i\)。从 \(pos_r\) 开始在 \(\mathrm{link}\) 树上倍增找到最浅的,\(\rm len\) 值 \(\geq r - l + 1\) 的状态 \(p\) 即为所求。
2.7.4 其它结论
- 在 \(\rm link\) 树上,若 \(p\) 是 \(q\) 的祖先,则 \(\mathrm{substr}(p)\) 中所有字符串在 \(\mathrm{longest}(q)\)(下记为 \(s\))中出现次数与出现位置相同。具体证明见 CF700E 题解区。
2.8 注意点总结
- 做题时不要忘记初始化 \(las\) 和 \(cnt\)。
- 第二个
while不要写成son[p][it] = cur,应为son[p][it] = cl。 - SAM 开两倍空间。
- 对于多串 SAM,如果每插入一个新字符串时令 \(las\gets T\),且插入字符时不特判 \(\delta(las, s_i)\) 是否存在,会导致出现空状态,从而父节点的 \(\mathrm{len}\) 值 不一定严格小于 子节点,使得桶排失效。对此要格外注意。
2.9 例题
I. P3804 【模板】后缀自动机 (SAM)
对 \(s\) 建出 SAM,对于每个状态 \(p\) 求出其 \(\mathrm{endpos}\) 集合大小。根据题目限制,答案即 \(\sum_{\\ \mathrm{|endpos}(p)|\geq 2}\mathrm{len}(p)\times |\mathrm{endpos}(p)|\)。视字符集大小为常数,时间复杂度线性。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define cpy(x, y, s) memcpy(x, y, sizeof(x[0]) * (s))
const int N = 2e6 + 5; // 不要忘记开两倍空间
const int S = 26;
char s[N];
int cnt = 1, las = 1;
int son[N][S], len[N], fa[N];
int ed[N], buc[N], id[N];
ll n, ans;
void ins(char s) {
int it = s - 'a', cur = ++cnt, p = las;
las = cur, len[cur] = len[p] + 1, ed[cur] = 1;
while(!son[p][it]) son[p][it] = cur, p = fa[p];
if(!p) return fa[cur] = 1, void();
int q = son[p][it];
if(len[p] + 1 == len[q]) return fa[cur] = q, void();
int cl = ++cnt; cpy(son[cl], son[q], S);
len[cl] = len[p] + 1, fa[cl] = fa[q], fa[q] = fa[cur] = cl;
while(son[p][it] == q) son[p][it] = cur, p = fa[p];
}
int main() {
scanf("%s", s + 1), n = strlen(s + 1);
for(int i = 1; i <= n; i++) ins(s[i]);
for(int i = 1; i <= cnt; i++) buc[len[i]]++;
for(int i = 1; i <= n; i++) buc[i] += buc[i - 1];
for(int i = cnt; i; i--) id[buc[len[i]]--] = i;
for(int i = cnt; i; i--) ed[fa[id[i]]] += ed[id[i]];
for(int i = 1; i <= cnt; i++) if(ed[i] > 1) ans = max(ans, 1ll * ed[i] * len[i]);
cout << ans << endl;
return 0;
}
II. P4070 [SDOI2016]生成魔咒
非常裸的 SAM,插入每个字符后新增的子串个数为 \(\mathrm{len}(cur) - \mathrm{len}(\mathrm{link}(cur))\),求和即可。由于字符集太大,需要使用 map 存转移数组。时间复杂度线性对数。
*III. P4022 [CTSC2012]熟悉的文章
首先二分答案 \(m\),考虑设 \(f_i\) 表示文章的 \(i\) 前缀最长的符合限制的匹配长度。根据应用 2.5.2 我们可以求出文章的每个前缀作为字典子串出现的最长后缀长度 \(L_i\),则 \(f_i = \max\limits_{j \in [i - L_i, i - m]} f_j + (i - j)\)。显然,\(L_i \leq L_{i - 1} + 1\),因此 \(i - L_i\) 单调不降,故可以使用单调队列优化。时间复杂度线性对数。
IV. P5546 [POI2000]公共串
建出 GSAM 后,设 \(msk_i\) 表示 \(\mathrm{substr}(i)\) 在哪些串中出现过,以状压形式存储,直接在 \(\mathrm{link}\) 树上合并即可。
V. P3346 [ZJOI2015]诸神眷顾的幻想乡
由于叶子节点仅有 \(20\) 个,因此从每个叶子节点开始,整棵树都会形成一个字典树。将这 \(20\) 棵 Trie 树拼在一起求 GSAM 就做完了。
VI. P3181 [HAOI2016]找相同字符
建出两个串的 GSAM,设 \(ed_{1, i}\) 表示状态 \(i\) 关于 \(s_1\) 的 \(\mathrm{endpos}\) 集合大小,\(ed_{2,i}\) 同理。答案显然为 \(\sum ed_{1, i}\times ed_{2, i}\times (\mathrm{len}(i) - \mathrm{len}(\mathrm{link}(i)))\)。
VII. P5341 [TJOI2019]甲苯先生和大中锋的字符串
建出 \(s\) 的 SAM 后容易得到所有出现 \(k\) 次的子串状态。每个符合题意的状态的子串长度是一段区间,差分即可。时间复杂度线性。
VIII. P4341 [BJWC2010]外星联络
SAM 的转移函数刻画了一个字符串 \(s\) 的所有子串,因此直接在该 DAG 上贪心遍历即可。贪心指优先走字符小的出边。
*IX. P3975 [TJOI2015]弦论
根据一条路径表示一个子串的性质,考虑求出从每个节点开始的路径条数 \(d_i = 1 + \sum_\limits{\delta(i, c)} d_{\delta(i, c)}\) 帮助跳过不可能的分支,然后在 SAM 的 DAG 上模拟跑一遍即可。对于 \(t = 1\) 只需将上式中的 \(1\) 改为 \(ed_i\)。
*X. H1079 退群杯 3rd E.
给定字符串 \(s\),多次询问求 \(s_{c\sim d}\) 有多少个子串包含 \(s_{a\sim b}\)。\(|s|, q \leq 2 \times 10 ^ 5\)。
设 \(L = b - a + 1\)。我们对每个位置 \(p \in [c + L - 1, d]\),求出有多少个左端点 \(l \geq c\) 使得 \(s_{l \sim p}\) 包含 \(s_{a\sim b}\)。考虑找到 \(p\) 前面 \(s_{a\sim b}\) 的最后一次出现位置 \(q\),则贡献显然为 \(\max(0, (q - L + 1) - c + 1)\)。
转化贡献形式,考虑每个落在 \([c + L - 1, d]\) 的 \(s_{a\sim b}\) 的出现位置 \(q\) 对答案的贡献。为方便说明,我们不妨假设 \(s_{a\sim b}\) 在 \(d + 1\) 处出现。考虑 \(s_{a\sim b}\) 在 \(q\) 之后的下一次出现 \(q'\),则对于 \(p\in [q, q' - 1]\),贡献均为 \((q - L + 1) - c + 1\)。注意到 \(2 - c - L\) 均与询问有关,与 \(q\) 无关,因此提出。则贡献可写为 \(q \times (q' - q)\)。即每个位置的下标值乘以和下一次出现之间的距离。线段树维护区间出现位置最小值,最大值即可维护该信息。
\(2 - c - L\) 的贡献次数为 \(d - (\min q) + 1\),因为所有 \([q, q' - 1]\) 的区间并起来形成了区间 \([\min q, d]\)。对 \(\rm endpos\) 集合 可持久化 线段树合并,再使用 2.7.3 的技巧,即可做到 \(\log\) 时间内回答每个询问。时间复杂度线性对数。代码。
XI. CF316G3 Good Substrings
对所有串建出 GSAM,求出每个状态所表示的串在 \(s\) 和每个模式串中出现了多少次,若合法则统计答案即可。时间复杂度线性。
如果用先建出字典树再建 GSAM 的方法,空间开销会比较大,需要用 unsigned short 卡空间。
XII. SP8222 NSUBSTR - Substrings
这就属于 SAM 超级无敌大水题了吧。
XIII. 某模拟赛 一切的开始
给定字符串 \(s\),求其两个 不相交 子串的长度乘积最大值,满足其中一个子串为另一个子串的子串。\(|s| \leq 10 ^ 5\)。
对 \(s\) 建出 SAM,对于每个状态 \(i\),我们只关心其第一次出现 \(a\) 和最后一次出现的位置 \(b\),因为这样最优,反证法可证。若前者是后者的子串,那么后者显然取满 \([a + 1, n]\),前者长度即 \(L = \min(\mathrm{len}(i), b - a)\)。若后者是前者的子串,则后者一定尽量长,长度为 \(L\),那么前者取满 \([1, b - L]\) 最优,长度即 \(b - L\)。
综上,答案即 \(\max\limits_i L \times \max(n - a, b - L)\)。时间复杂度线性。
*XIV. CF1037H Security
考虑直接在后缀自动机的 DAWG 上贪心。使用线段树合并判断当前字符串是否作为 \([l, r]\) 的子串出现过,时间复杂度 \(\mathcal{O}(|\Sigma|n\log n)\)。代码。
*XV. CF700E Cool Slogans
容易发现 \(s_{i - 1}\) 在 \(s_i\) 中一定同时以前缀和后缀的形式出现,否则调整法证明可以做到更优。我们使用 \(s_{i - 1}\) 在 \(s_i\) 中作为后缀的性质,考虑直接在 \(\rm link\) 树上 DP。
再根据 2.7.4 的结论一(实际上这个结论是笔者做本题时才遇到的),我们可以设 \(f_p\) 表示 \(\mathrm{longest}(p)\) 的答案,以及 \(g_p\) 表示 \(p\) 的祖先中答案取到 \(f_p\) 的深度最小的状态,因为我们要让串长尽可能小,这样出现次数更多。转移即检查 \(\mathrm{longest}(g_{\mathrm{link}(p)})\) 在 \(\mathrm{longest}(p)\) 中是否出现了至少两次,这相当于检查 \(\mathrm{longest}(g_{\mathrm{link}(p)})\) 是否在 \(\mathrm{longest}(p)\) 的某个出现位置 \(pos\) 之前的一段区间 \([pos - \mathrm{len}(p) + \mathrm{len}(g_{\mathrm{link}(p)}), pos - 1]\) 处出现,容易用线段树合并维护 \(\rm endpos\) 集合做到。若是,则令 \(f_p = f_{\mathrm{link}(p)} + 1\),\(g_p = p\)。否则 \(f_p = f_{\mathrm{link}(p)}\),\(g_p = g_{\mathrm{link}(p)}\)。
\(\max f_p\) 即为答案,时空复杂度线性对数。代码。
*XVI. CF666E Forensic Examination
SAM 各种常用技巧结合版。首先对 \(s\) 和 \(t_i\) 一并建出 GSAM,线段树维护每个节点对应的子串在每个 \(t_i\) 中出现的次数,即线段树 \(T_p\) 的位置 \(i\) 上记录着 \(p\) 所表示的所有串在 \(t_i\) 中的出现次数。由于题目还需求最小编号,所以线段树维护区间最大出现次数以及对应最小编号。
使用线段树合并,预处理 \(\rm link\) 的倍增数组以快速定位子串,单次询问只需倍增到 \(s[pl, pr]\) 的对应状态 \(p\),查询 \(T_p\) 上 \([l, r]\) 的信息即可。时空复杂度均为线性对数。代码。
2.10 相关链接与资料
- OI wiki:后缀自动机(SAM)。
- hihoCoder:后缀自动机一。
- hihoCoder:后缀自动机二。
- Linshey:对 SAM 和 PAM 的一点理解。
- 洛谷题单:SA & SAM。
- 辰星凌:题解 P6139 【模板】广义后缀自动机(广义SAM)。
3. 回文自动机 PAM
省选前两周填坑。之所以不是省选之后是因为担心省选考这玩意。