圆方树基础知识梳理

腾云今天首飞了吗转载文章 2023-04-02 63 0 原文

由于树有不具有环等性质，在树上处理信息往往比在图上处理信息更加方便。圆方树就是这样一种把图转换成树的方法/思想，由此达到更便捷地维护图上信息，处理图上问题的目的。

仙人掌

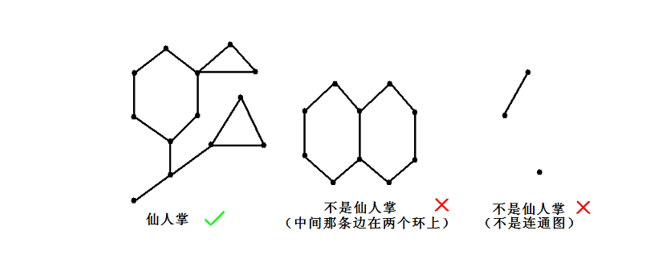
仙人掌是满足每条边处于不超过一个简单环的无向连通图。

圆方树

*这里讨论的圆方树为广义圆方树。
对于一个仙人掌，该仙人掌中原有的点称为圆点。任意选定一个圆点，钦定它为树根开始 \(dfs\)，找出图中的所有点双连通分量，对于每个点双连通分量，新建一个方点，将该方点与点双连通分量里的所有点连一条边，删除原图上的所有边，如此便能得到一个树形结构。这棵树叫做圆方树。求点双连通分量还是用 \(tarjan\) 算法，在此基础上稍作修改即可。
\(Code:\)

void tarjan(int u) {
	low[u] = dfn[u] = ++tim;
	s[++s[0]] = u;
	++si;
	for (int i = head[u]; i; i = edge[i].next) {
		int v = edge[i].v;
		if (!dfn[v]) {
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if (low[v] == dfn[u]) {
				wgh[++cnt] = 0;
				for (int x = 0; x != v; --s[0]) {
					x = s[s[0]];
					t[cnt].push_back(x);
					t[x].push_back(cnt);
					++wgh[cnt];
				}
				t[cnt].push_back(u);
				t[u].push_back(cnt);
				++wgh[cnt];
			}
		} else low[u] = min(low[u], dfn[v]);
	}
}

显然，圆方树中方点与方点之间肯定没有边，圆点与圆点之间也肯定没有边。

既好想又好写，不是吗？然而它有什么用呢？

应用

仙人掌最短路：

多次询问仙人掌上两点 \((u,v)\) 的最短路，要求路径是简单路径。

先考虑下在仙人掌上怎么从 \(u\) 走到 \(v\)：有树边就走树边，有环的话两个方向走都可以。因此先随便钦定一个根，对每个 \(u\) 记录一个 \(top[u]\) 表示从 \(u\) 走到 \(u\) 所在环的根节点的最短路径长度，大概搞搞就可以出答案了——当然，这个方法实现起来比较复杂，我们把这个想法搬到圆方树上试试看。

如果 \(u\)，\(v\) 在圆方树上的 \(lca\) 是圆点的话，最短路显然就是二者树上的距离。
如果 \(u\)，\(v\) 在圆方树上的 \(lca\) 是方点的话，设 \(fau\) 为他们 \(lca\) 的一个子节点，\(u\) 在以 \(fau\) 为根的子树中，同理也设一个 \(fav\)。那么最短路就是树上 \(u\) 到 \(fau\) 的最短距离 + 树上 \(v\) 到 \(fav\) 的最短距离 + 环上 \(fav\) 到 \(fau\) 的最短距离。