排列组合

恒等式

(1) \(C_n^m=C_n^{n-m}\)

从\(n\)个元素选择\(m\)个，等价于\(n\)个元素中不选\(n-m\)个。

(2) \(A_n^m+mA_n^{m-1}=A_{n+1}^m\)

在\(n+1\)个元素中选择\(m\)个元素排成一排，等价于考虑第\(n+1\)个元素：

1. 不在该排列中：\(A_n^m\)
2. 存在该排列中：\(mA_n^{m-1}\)，\(m\)表示该元素有\(m\)种放置位置。

(3) \(C_n^{m-1}+C_n^{m}=C_{n+1}^m \ or \ C_{n-1}^{m-1}+C_{n-1}^m=C_n^m\)

在\(n+1\)个元素中选出\(m\)个元素，等价于考虑第\(n+1\)个元素：

1. 不在该组合中：\(C_n^m\)
2. 存在该组合中：\(C_n^{m-1}\)

(3*) \(\sum_{i=m}^nC_i^m=C_m^m+C_{m+1}^m+C_{m+2}^m+\cdots+C_{n-1}^m+C_n^m=C_{n+1}^{m+1}\)

可由式\((3)\)推导而出。

\(C_{m+1}^{m+1}=1=C_{m}^{m}\)

\(C_{m}^{m}+C_{m+1}^{m}=C_{m+1}^{m+1}+C_{m+1}^m=C_{m+2}^{m+1}\)

\(C_{m+2}^{m+1}+C_{m+2}^m=C_{m+3}^{m+1}\)

\(\cdots\)

\(C_{n}^{m+1}+C_n^m=C_{n+1}^{m+1}\)

得证。

事实上式\((3)\)可以认为是在杨辉三角上的递推。所以该式也可以由杨辉三角进行理解（如图）。

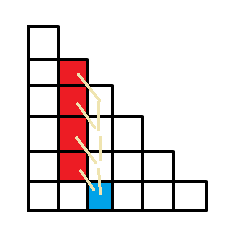
事实上很多恒等式都可以直接利用杨辉三角进行（眼睛上的）理解推导（）

(4) \(C_n^{m-1}+2C_n^m+C_n^{m+1}=C_{n+2}^{m+1}\)

从\(n+2\)个元素中选出\(m+1\)个元素，考虑第\(n+1\)个元素和第\(n+2\)个元素：

1. 两元素都不在该组合中：\(C_n^{m+1}\)
2. 两元素都在该组合中：\(C_n^{m-1}\)
3. 两元素有一个在该组合中：\(2C_n^m\)

(5) \(C_a^b \times C_b^c=C_a^c \times C_{a-c}^{b-c}=C_a^c \times C_{a-c}^{a-b}\)

考虑在集合\(A'\)，\(|A'|=a\)中，求构造集合\(C' \subseteq B' \subseteq A'\)，\(|C'|=c,|B'|=b\)的方案数。

1. 先从\(A'\)中\(a\)个元素中取出\(b\)个元素放入\(B'\)，再从\(B'\)中取出\(c\)个元素放入\(C'\)：\(C_a^b \times C_b^c\)
2. 先从\(A'\)中\(a\)个元素中取出\(c\)个元素放入\(C'\)（当然同时也放进了\(B '\)），再从剩下的\(a-c\)个元素中取出\(b-c\)个元素放入\(\complement_{B'}C'\)中：\(C_a^c \times C_{a-c}^{b-c}\)

(6) \(\sum_{i=0}^{a}C_n^iC_m^{a-i}=C_n^0C_m^a+C_n^1C_m^{a-1}+\cdots+C_n^{a-1}C_m^1+C_n^aC_m^0=C_{n+m}^a\)

在\(n+m\)个元素中选出\(a\)个元素：

• 前\(n\)个元素中选择了\(i\)个元素，后\(m\)个元素中选择了\(a-i\)个元素：\(C_n^iC_m^{a-i}\)

特别地，当\(m=n\)时：

\(\sum_{i=0}^aC_n^iC_n^{a-i}=C_{2n}^a\)

又根据\(C_n^i=C_n^{n-i}\)，当\(a=n\)时：

\(\sum_{i=0}^n(C_n^i)^2=C_{2n}^n\)

多重集合（全）排列数

设可重集\(S=\{n_1 \cdot a_1,\cdots,n_k \cdot a_k \}\)

\(S\)的全排列数为：

$$\frac{n!}{n_1! \cdots n_k!}$$

将\(m\)个相同物品放入\(n\)个相同盒子 || 将正整数\(m\)划分成\(n\)个正整数的和

1.当作容量为\(n\)，物品大小为\(1 \dots m\)的完全背包。

2.设\(f_{i,j}\)表示将正整数\(i\)划分为\(j\)个正整数之和的方案数：\(f_{i,j}=f_{i-1,j-1}+f_{i,j-i}\)

Catalan数

一些等价的Catalan数相关问题例：

0. 入栈序列为\(1 \dots n\)的出栈序列种数；
1. （基本模型）将\(n\)个\(0\)和\(n\)个\(1\)排成任意前缀\(0\)的个数不少于\(1\)的个数的序列数量；
2. \(n\)个左括号和\(n\)个右括号组成的合法括号序列个数；
3. \(n\)个节点构成的不同二叉树数量；
4. 平面直角坐标系中从原点\((0,0)\)出发到\((2n,0)\)，每一步可以向正右上或正右下移动，并且路径不经过第四象限的方案数
5. \(\dots\)

使用例\((3)\)来说明，对\(n\)个节点构成二叉树数量的一种\((0)\)的理解：入栈后继续入栈为左儿子，直接出栈为没有左儿子；出栈后入栈为右儿子，直接出栈为没有右儿子。

其实这个问题的原本理解是：已知先序遍历，求构造中序遍历的方案数。

当然也可以理解为一个递推：设\(Cat_i\)表示\(i\)个节点构成二叉树的数量，那么有\(Cat_i=\sum_{j=0}^i Cat_j \times Cat_{i-j}\)

现在用例\((4)\)来说明：

平面直角坐标系中从原点\((0,0)\)出发到\((2n,0)\)，每一步可以向正右上或正右下移动，并且路径不经过第四象限的方案数

也即有\(n\)个向右上的操作，\(n\)个向右下的操作。

可以考虑用所有的方案（\(C_{2n}^n\)）减去不合法的（经过第四象限的方案）

每个不合法的方案必定经过直线\(y=-1\)。将这样每个方案第一个与该直线相交的点之后的整段路径，会得到唯一对应的一条终点为\((2n,-2)\)的路径。

也就是从\((0,0)\)到\((2n,-2)\)的每一条路径都对应了一条原问题不合法的路径。

所以答案即\(Cat_n=C_{2n}^n-C_{2n}^{n-1}\)

zzx：另外还有\(Cat_n=\frac{C^{n}_{2n}}{n+1}\)