朴素贝叶斯算法(Naive Bayes, NB) 是应用最为广泛的分类算法之一,它是基于贝叶斯定义和特征条件独立假设的分类器方法。朴素贝叶斯法基于贝叶斯公式计算得到,有着坚实的数学基础,以及稳定的分类效率;NB模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单,当年的垃圾邮件分类都是基于朴素贝叶斯分类器识别的。朴素贝叶斯名字中的“朴素”二字代表着该算法对概率事件做了很大的简化,简化内容就是各个要素之间是相互独立的。比如今天刮风和气温低,两个要素导致了不下雨的结果。实际上刮风可能导致气温低,而且刮风对于天晴的影响会更大,朴素贝叶斯认为刮风和气温之间相互独立,且对于是否下雨这个结果的影响没有轻重之分。

一、贝叶斯决策理论
贝叶斯决策基于概率和误判损失来选择最优的类别标记。本部分内容将从以下问题导出:对于样本\(x\),有\(N\)种可能的类别标记,即类别空间\(y=\{c_1,c_2,\cdots ,c_N\}\)。\(\lambda_{ij}\)表示将一个真实标记为\(c_j\)的样本误分类为\(c_i\)所产生的损失。基于后验概率\((c_i|x)\)(即对于给定样本,判断样本属于哪个分类,概率最大的那个类别是最可能正确的类别)可获得将样本\(x\)分类为\(c_i\)所产生的期望损失,即在样本\(x\)上的“条件风险”:
\]
我们训练模型的目的就是为了寻找一个映射函数\(h:x\rightarrow y\)以最小化总体风险:
\]
那么对于每个样本\(x\),若\(h(x)\)能最小化条件风险\((h(x)|x)\),则总体风险\(R(h)\)也将被最小化。所以为了得到最小的总体风险,只需在每个样本上选择哪个能使条件风险\(R(c∣x)\)最小的类别标记,即
\]
其中\(h^*\)称为贝叶斯最优分类器,与之对应的总体风险\(R(h^*)\)称为贝叶斯风险。\(1-R(h^*)\)反映了分类器所能达到的最好性能,即通过机器学习所产生的模型精度的理论上限。
若\(R(c|x)\)是最小化分类错误率,则误判损失\(\lambda_{ij}\)可表示为:
\]
此时条件风险表示为:$$R(c|x)=1-P(c|x)$$
于是,最小化分类错误率的贝叶斯最优分类器为:
\]
即对每个样本\(x\),选择能使后验概率\(P(c∣x)\)最大的类别标记。
【贝叶斯模型的解释】
以上内容已经对问题解释的很清楚了,如果想要对样本进行分类,我们需要得到最大的\(P(c|x)\),但是对于一般的情况下,直接求解,很难求出,所以一般借助贝叶斯定理,从侧面进行求解:
\]
\(P(c|x)\)叫后验概率,也就是我们要计算的后验概率,知道样本,计算这个样本属于某个类别的概率,概率最大的那个类别是最可能正确的类别。
\(P(c)\)是类“先验”概率。
\(P(x∣c)\)是条件概率,也就是在类别\(c\)的条件下,出现样本\(x\)的可能性。
对于每个样本\(x\),其\(P(x)=\frac{x的样本数}{总样本数}\)为恒定的数值(在不考虑特征属性的情况下,如此表示),所以计算\(P(c∣x)\)的难点在于求解\(P(x∣c)\)或称之为“似然函数”。
求解类别\(c\)的类条件概率\(P(x∣c)\)(似然函数)有两种方式实现:
- 极大似然估计
- 朴素贝叶斯分类器
二、朴素贝叶斯算例
2.1 朴素贝叶斯分类案例分析
案例:采用西瓜数据集3.0进行举例
| 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|---|---|---|---|---|
| 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.46 | 是 |
| 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 0.774 | 0.376 | 是 |
| 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.634 | 0.264 | 是 |
| 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 0.608 | 0.318 | 是 |
| 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.556 | 0.215 | 是 |
| 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 0.403 | 0.237 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 0.481 | 0.149 | 是 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 0.437 | 0.211 | 是 |
| 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 0.666 | 0.091 | 否 |
| 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 0.243 | 0.267 | 否 |
| 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 0.245 | 0.057 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 0.343 | 0.099 | 否 |
| 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 0.639 | 0.161 | 否 |
| 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 0.657 | 0.198 | 否 |
| 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 0.36 | 0.37 | 否 |
| 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 0.593 | 0.042 | 否 |
| 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 0.719 | 0.103 | 否 |
其中类先验概率\(P(c)\)为:
\]
\]
然后,每个属性的似然概率(条件概率)\(P(x_i|c)\)为:
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
\]
| 条件(似然)概率 | 是(好瓜) | 否(好瓜) |
|---|---|---|
| 青绿(色泽) | \(P_{青绿|是}=P({色泽=青绿|好瓜=是})=\frac{3}{8}=0.375\) | \(P_{青绿|否}=P({色泽=青绿|好瓜=否})=\frac{3}{9}=0.333\) |
| 乌黑(色泽) | \(P_{乌黑|是}=P({色泽=乌黑|好瓜=是})=\frac{4}{8}=0.500\) | \(P_{乌黑|否}=P({色泽=乌黑|好瓜=否})=\frac{2}{9}=0.222\) |
| 浅白(色泽) | \(P_{浅白|是}=P({色泽=浅白|好瓜=是})=\frac{1}{8}=0.125\) | \(P_{浅白|否}=P({色泽=浅白|好瓜=否})=\frac{4}{9}=0.444\) |
于是,根据朴素贝叶斯公式可得:
\]
\]
由于\(0.063>6.80\times10^{-5}\),因此,预测结果为“好瓜”。
2.2 拉普拉斯修正
若某个属性值在训练集中没有与某个类同时出现过,则直接基于朴素贝叶斯进行估计,很有很能出现错误的估计:例如:对一个“敲声=清脆”的测试例,有
\]
为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”,在估计概率值时通常要进行“平滑”,常用“拉普拉斯修正”,令\(N\)表示训练集\(D\)中可能的类别数,\(N_i\)表示第\(i\)个属性可能的取值数,则修正后的\(P(c)\)和\(P(xi∣c)\)如下
\]
\]
& P_\lambda\left(y=c_n\right)=\frac{\sum_{i=1}^N I\left(y_i=c_n\right)+\lambda}{N+K \lambda}, n=1,2, \ldots, K \\
& P_\lambda\left(x^j=a_j \mid y=c_n\right)=\frac{\sum_{i=1}^N I\left(x_i^j=a_j \mid y=c_n\right)+\lambda}{\sum_{i=1}^N I\left(y_i=c_n\right)+S_j \lambda}
\end{aligned}
\]
| Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(x^1\) | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
| \(x^2\) | S | M | M | S | S | S | M | M | L | L | L | M | M | L | L |
| y | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
\]
因为 \(P(y=1)=\frac{9+1]}{15+\left[2^*[1]\right.}[2\) 表示 \(y\) 有 2 个取值, 1 为 \(\lambda]\)
\]
\]
因此 \(P(x=(2, S) \mid y=1)=\frac{10}{17} * \frac{4}{12} * \frac{2}{12}=\frac{5}{153}\)
\]
因为 \(P(y=-1)=\frac{6+[1]}{15+[2]^*[1]}[2\) 表示 \(y\) 有 2 个取值, 1 为 \(\lambda]\)
\]
\]
因此 \(P(x=(2, S) \mid y=-1)=\frac{7}{17} * \frac{3}{9} * \frac{4}{9}=\frac{28}{459}\)
三、朴素贝叶斯的R实现
#构造训练集
data <- matrix(c("sunny","hot","high","weak","no",
"sunny","hot","high","strong","no",
"overcast","hot","high","weak","yes",
"rain","mild","high","weak","yes",
"rain","cool","normal","weak","yes",
"rain","cool","normal","strong","no",
"overcast","cool","normal","strong","yes",
"sunny","mild","high","weak","no",
"sunny","cool","normal","weak","yes",
"rain","mild","normal","weak","yes",
"sunny","mild","normal","strong","yes",
"overcast","mild","high","strong","yes",
"overcast","hot","normal","weak","yes",
"rain","mild","high","strong","no"), byrow = TRUE,
dimnames = list(day = c(),
condition = c("outlook","temperature",
"humidity","wind","playtennis")), nrow=14, ncol=5);
#计算先验概率
prior.yes = sum(data[,5] == "yes") / length(data[,5]);
prior.no = sum(data[,5] == "no") / length(data[,5]);
#模型
naive.bayes.prediction <- function(condition.vec) {
# Calculate unnormlized posterior probability for playtennis = yes.
playtennis.yes <-
sum((data[,1] == condition.vec[1]) & (data[,5] == "yes")) / sum(data[,5] == "yes") * # P(outlook = f_1 | playtennis = yes)
sum((data[,2] == condition.vec[2]) & (data[,5] == "yes")) / sum(data[,5] == "yes") * # P(temperature = f_2 | playtennis = yes)
sum((data[,3] == condition.vec[3]) & (data[,5] == "yes")) / sum(data[,5] == "yes") * # P(humidity = f_3 | playtennis = yes)
sum((data[,4] == condition.vec[4]) & (data[,5] == "yes")) / sum(data[,5] == "yes") * # P(wind = f_4 | playtennis = yes)
prior.yes; # P(playtennis = yes)
# Calculate unnormlized posterior probability for playtennis = no.
playtennis.no <-
sum((data[,1] == condition.vec[1]) & (data[,5] == "no")) / sum(data[,5] == "no") * # P(outlook = f_1 | playtennis = no)
sum((data[,2] == condition.vec[2]) & (data[,5] == "no")) / sum(data[,5] == "no") * # P(temperature = f_2 | playtennis = no)
sum((data[,3] == condition.vec[3]) & (data[,5] == "no")) / sum(data[,5] == "no") * # P(humidity = f_3 | playtennis = no)
sum((data[,4] == condition.vec[4]) & (data[,5] == "no")) / sum(data[,5] == "no") * # P(wind = f_4 | playtennis = no)
prior.no; # P(playtennis = no)
return(list(post.pr.yes = playtennis.yes,
post.pr.no = playtennis.no,
prediction = ifelse(playtennis.yes >= playtennis.no, "yes", "no")));
}
#预测
naive.bayes.prediction(c("rain", "hot", "high", "strong"));
naive.bayes.prediction(c("sunny", "mild", "normal", "weak"));
naive.bayes.prediction(c("overcast", "mild", "normal", "weak"));
四、朴素贝叶斯决策的判断准则
设$\omega_1 $代表正常细胞, \(\omega_2\)代表异常细胞(癌细胞)。
$$ P(X)=\sum_{j=1}^{c} P(X|\omega_j)P(\omega_j)\quad c表示总类别数$$
先验概率:预先已知的或者可以估计的模式识别系统位于某种类型的概率。 \(P(\omega_1),P(\omega_2)\)称为先验概率,根据统计资料估计得到,
P ( ω 1 ) + P ( ω 2 ) = 1 P ( ω 1 ) > P ( ω 2 ) $$P(\omega_1)+P(\omega_2)=1\\ P(\omega_1)>P(\omega_2)$$
类条件概率:系统位于某种类型条件下模式样本\(x\)出现的概率。\(P(x|\omega_1),P(x|\omega_2)\)称为类条件概率,根据训练样本统计分析得到。
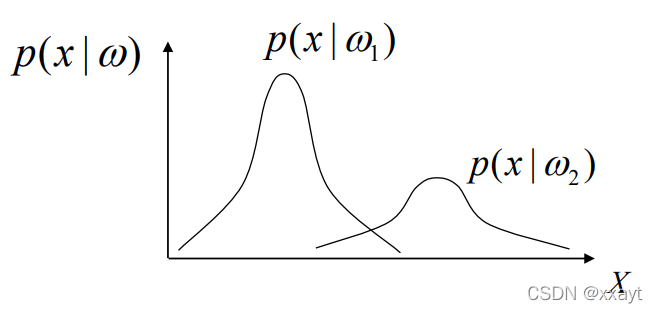
后验概率:系统在某个具体的模式样本 \(x\)条件下位于某种类型的概率,可根据贝叶斯公式计算,用作分类判决的依据。\(P(\omega_1|x),P(\omega_2|x)\) 称为后验概率,
\]
联合概率:\(P(X,\omega_i)\)
贝叶斯决策:在类条件概率密度和先验概率已知的情况下,通过贝叶斯公式比较样本属于两类的后验概率,为使总体错误率最小,将类别决策为后验概率大的一类。
\]
4.1 最小错误率贝叶斯决策
模式特征 \(X\): \(d\)维特征向量 $X = [ x_1 , x_2 , . . . , x_d ]^T $
分类错误的概率 \(P(e|x)\):是模式特征\(X\) 的函数
\]
平均错误率\(P(e)\):是随机函数 \(P(e|x)\)的期望
$$P(e)=\int P(e|x)P(x)dx$$
最小错误率:
若 \(P(\omega_k|x)=\max_{i=1,2}P(\omega_i|x)\),则$x\in \omega_k $
例题:以两类问题(癌细胞与正常细胞的分类)为例。
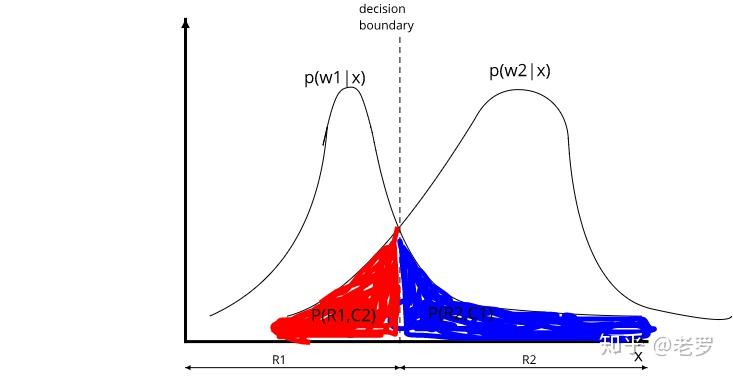
解:假设根据某种分类规则,模式(特征)空间被分成两个部分(以 \(H\)为分界面)其中\(R_1\)中的样本被分为第一类,\(R_2\)中的样本被分为第二类。
已知先验概率\(P(\omega_1),P(\omega_2)\),根据数据得到类条件概率\(P(x|\omega_1),P(x|\omega_2)\)。 利用贝叶斯公式得到后验概率\(P(\omega_1|x),P(\omega_2|x)\)

当 \(P(\omega_1|x)=P(\omega_2|x)\) 时的分界线称为决策边界或分类线。
计算错误率:
第一类样本分类错误率:\(\int_{R_2} P(x|\omega_1)P(\omega_1)dx\)
第二类样本分类错误率:\(\int_{R_1} P(x|\omega_2)P(\omega_2)dx\)
平均分类出错率:
P(x|\omega_2)P(\omega_2)dx\\
=\int_{R_2} P(\omega_1|x)P(x)dx+\int_{R_1} P(\omega_2|x)P(x)dx \quad 平均分类出错率 \\
P(\omega_1)=\int_{R_2} P(\omega_1|x)P(x)dx+\int_{R_1} P(\omega_1|x)P(x)dx \quad 全概率公式\\
P(e)=P(\omega_1)+\int_{R_1} (P(\omega_2|x)-P(\omega_1|x))P(x)dx
\]
当\(R_1\)中的样本满足\(P(\omega_2|x)<P(\omega_1|x)\)时,\(P(e)\)取得最小值。即当$ P(\omega_2|x)=P(\omega_1|x)$时,错误率最小。
4.2 最小风险的贝叶斯决策
样本\(X\):\(d\)维随机向量 \(X=[x_1,x_2,...,x_d]^T\)(构成自然空间)
类别\(w\):\(\Omega=\{\omega_1,\omega_2,...,\omega_c\}\) (构成状态空间\(\Omega\))
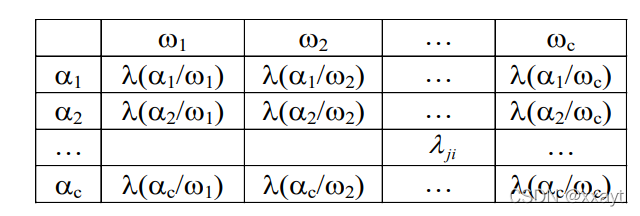
决策 \(\alpha\):分类时所采取的决定。决策\(\alpha_j\)表示将模式\(\vec{x}\) 指判为\(\omega_j\)或者拒判。
决策表:
损失函数:对于实际状态为\(\omega_j\)的向量\(\vec{x}\),采取决策\(\alpha_i\)所带来的损失
\]
若希望尽可能避免将状态\(\omega_j\)错判为\(\omega_i\) (即该分类错误损失较大),则可以将相应的\(\lambda_{ji}\)的值调大一些。
决策表:决策表的形成是困难的,需要大量的领域知识。决策表不同会导致决策结果的不同。
最小风险:把各种分类错误引起的损失考虑进去的贝叶斯决策法则,以使得期望的损失最小。
样本\(x\)的期望损失:通过对属于不同状态$\omega_j \(的后验概率\)P(\omega_j|x)$ 采取决策\(\alpha_i\)的期望损失(期望风险)
\]
最小风险:
若\(R(\alpha_k|x)=\min_{i=1,...,c}R(\alpha_i|x)\),则\(\alpha=\alpha_k\)
最小风险和最小错误率贝叶斯决策法则的关系:
两类最小错误率贝叶斯决策规则
\{ω1,ω2\}
\]
多类最小错误率贝叶斯决策规则
\]
多类最小风险贝叶斯决策规则
\]
总结
最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model,NBM)。和决策树模型相比,朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。同时,NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单。理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,这给NBC模型的正确分类带来了一定影响。朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化,即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重,也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。