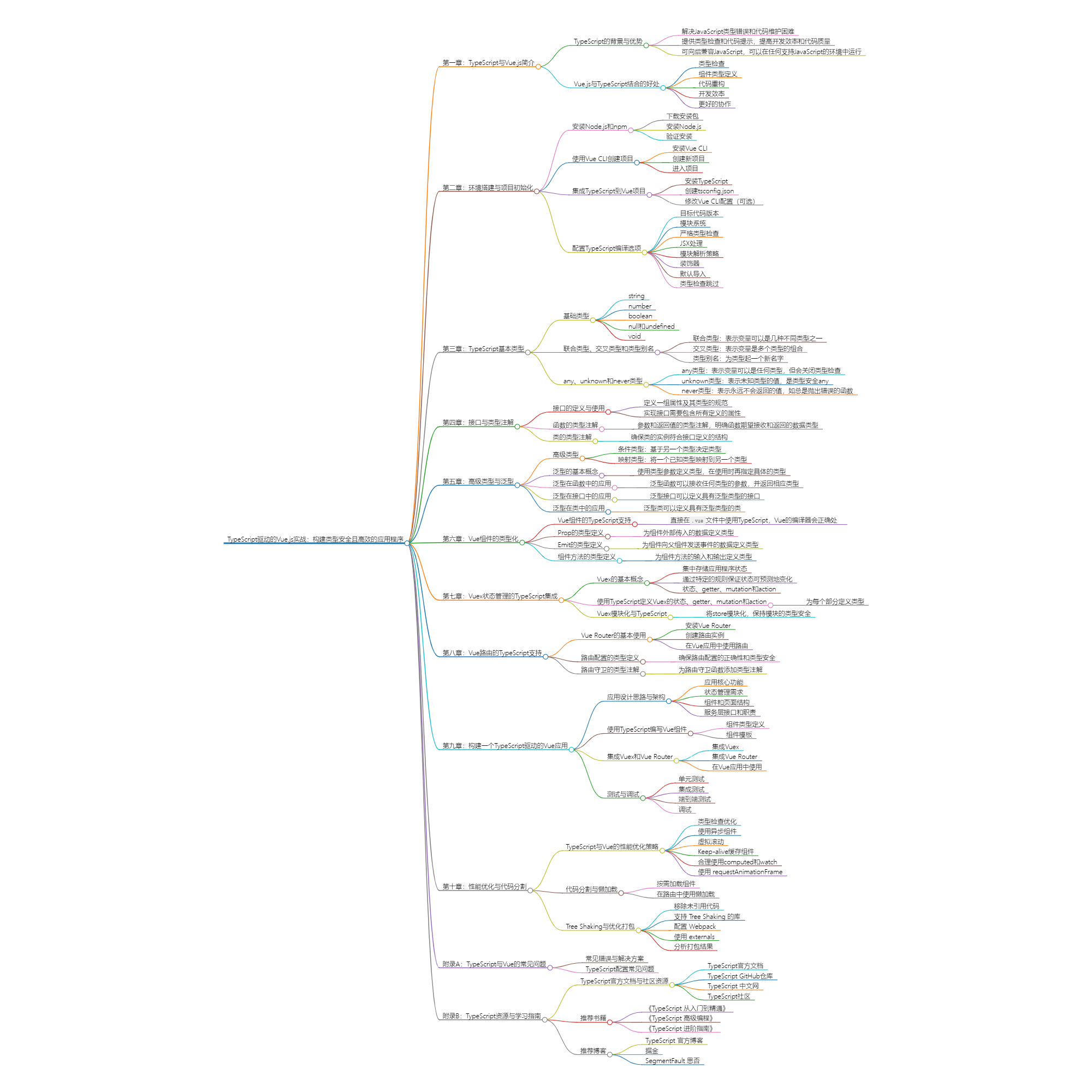
图的连通性
\(\text{By DaiRuiChen007}\)
一、割点与桥
I. 定义
在一张无向图 \(\mathbf G\) 上,如果删除某一条无向边 \((u,v)\) 会使得图中的极大连通分量(连通块)的数量增加,则称 \((u,v)\) 是 \(\mathbf G\) 中的一个桥(割边)
在一张无向图 \(\mathbf G\) 上,如果删除某一个点 \(u\) 和所有与它相连的边会使得图中的极大连通分量(连通块)的数量增加,则称 \(u\) 是 \(\mathbf G\) 中的一个割点
II. 求割点
用类似 tarjan 的算法求解割点,对于每个节点,记录其 dfn 序,用 \(low_u\) 表示在搜索树上以 \(u\) 为根的子树中,经过至多一条非树边后能到达的最小的 dfn 序值
对于某一个节点 \(u\),其为割点的充分必要条件是:搜索树上的存在一个 \(u\) 的儿子 \(v\) 满足 \(low_v\ge dfn_u\),也就是说 \(v\) 无论如何不经过 \(u\) 都不能到达 \(u\) 的祖先,如果删除点 \(u\),则搜索树上以 \(v\) 为根的子树会额外形成一个极大连通分量,则 \(u\) 必然是一个割点
特别地,如果 \(u\) 是搜索树的根节点,则满足条件的儿子 \(v\) 至少需要 \(2\) 个
参考代码如下:
inline void tarjan(int p,int lim) {
low[p]=dfn[p]=++dfncnt;
int siz=0;
for(int v:edge[p]) {
if(!dfn[v]) {
tarjan(v,1);
low[p]=min(low[p],low[v]);
if(low[v]>=dfn[p]) {
++siz;
if(siz>=lim) isCutVertex[p]=true;
}
} else low[p]=min(low[p],dfn[v]);
}
}
signed main() {
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,2);
}
III. 求桥
用类似 tarjan 的算法求解割点,对于每个节点,记录其 dfn 序,用 \(low_u\) 表示在搜索树上以 \(u\) 为根的子树中,经过至多一条非树边后能到达的最小的 dfn 序值
对于某一条边 \((u,v)\),其为桥的充分必要条件是:搜索树上 \(v\) 是 \(u\) 的儿子且满足 \(low_v> dfn_u\),也就是说 \(v\) 无论如何不经过 \((u,v)\) 都不能到达 \(u\) 的祖先,如果删除边 \((u,v)\),则搜索树上以 \(v\) 为根的子树会额外形成一个极大连通分量,则 \((u,v)\) 必然是一个桥
在记录 \(low_u\) 的时候,要特别注意不能从其搜索树上的父亲处转移最小 dfn 序,所以递归的时候要记录父亲防止错误转移
准确来说,我们的 \(low_u\) 不能从搜索树上的父亲到儿子的树边转移,不过如果图上出现重边,则我们会将 \((u,v)\) 之间的非树边当成树边切断转移
所以,在有重边的图上,我们不能通过记录父亲来防止 \((u,v)\) 连接,我们要记录搜索树上边的编号判断是否通过 \((u,v)\),通过链式前向星存边,将边的下标从 \(0/2\) 开始编号,这样对于每一条边,其反向边的编号就是其本身编号异或 \(1\)
参考代码如下(链式前向星从 \(2\) 开始编号)
inline void tarjan(int p,int uid) {
dfn[p]=low[p]=++dfncnt;
for(int i=head[p];i;i=edge[i].lst) {
int v=edge[i].des;
if(!dfn[v]) {
tarjan(v,i);
low[p]=min(low[p],low[v]);
if(low[v]>dfn[p]) edge[i].isBridge=edge[i^1].isBridge=true;
} else if(i!=(uid^1)) low[p]=min(low[p],dfn[v]);
}
}
signed main() {
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0);
}
二、强连通与强连通分量
I. 定义
一张有向图 \(\mathbf G\) 是强连通的,当且仅当 \(\mathbf G\) 中任意两个点都联通,而 \(\mathbf G\) 的强连通分量(SCC,Strongly Connected Components)是指 \(\mathbf G\) 的一个极大连通子图
II. 求强连通分量
我们维护每个节点的 dfn 序
用 \(low_u\) 维护每个节点能够到达的最小节点的 dfn 序,对于非树边直接更新当前节点的 \(low\) 值即可
不难发现每个 SCC 在搜索树中都是一个连通块,并且有且仅有一个节点 \(u\) 满足 \(dfn_u=low_u\),这个节点应该是这个 SCC 中第一个搜索到的节点,所以我们可以通过维护一个栈来将当前 SCC 中所有的节点取出
不过在搜索树中,可能有某些边影响将当前节点连向某个已经在其他 SCC 中的节点,我们只用栈内节点的 dfn 序更新 \(low\) 值
参考代码如下:
inline void tarjan(int p) {
low[p]=dfn[p]=++dfncnt;
st[++top]=p;
ins[p]=true;
for(int v:edge[p]) {
if(!dfn[v]) {
tarjan(v);
low[p]=min(low[p],low[v]);
} else if(ins[v]) low[p]=min(low[p],low[v]);
}
if(dfn[p]==low[p]) {
++scccnt;
int k;
do {
k=st[top--];
ins[k]=false;
bel[k]=scccnt;
} while(k!=p);
}
}
signed main() {
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
}
三、典例分析
I. [洛谷2860]Redundant Paths G
思路分析
显然,在一个 E-DCC(Edge-Double Connnected Components,边双连通分量)中的点都满足题意,所以我们可以对原图进行缩点,将每个 E-DCC 缩成一个点,最终会得到一棵树,我们可以考虑对于树上每个 E-DCC 如果其度数 \(\ge 2\),则不需要加边,我们可以每两个度数为 \(1\) 的 E-DCC连一条边,不妨设这一类的 E-DCC 共有 \(k\) 个,则答案为 \(\left\lceil\dfrac{k}{2}\right\rceil\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5001,MAXM=1e4+1;
struct node {
int des,lst;
bool isBridge;
} edge[MAXM<<1];
int low[MAXN],head[MAXN],dfn[MAXN],dfncnt,leaf,tot=1;
int bel[MAXN],edcccnt;
vector <int> g[MAXN];
inline void link(int u,int v) {
edge[++tot]=(node){v,head[u]};
head[u]=tot;
}
inline void tarjan(int p,int id) {
low[p]=dfn[p]=++dfncnt;
for(int i=head[p];i;i=edge[i].lst) {
int v=edge[i].des;
if(!dfn[v]) {
tarjan(v,i);
low[p]=min(low[p],low[v]);
if(low[v]>dfn[p]) edge[i].isBridge=edge[i^1].isBridge=true;
} else if(i!=(id^1)) low[p]=min(low[p],dfn[v]);
}
}
inline void build(int p) {
bel[p]=edcccnt;
for(int i=head[p];i;i=edge[i].lst) {
if(edge[i].isBridge||bel[edge[i].des]) continue;
build(edge[i].des);
}
}
inline void dfs(int p,int f) {
if(g[p].size()==1) ++leaf;
for(int v:g[p]) {
if(v==f) continue;
dfs(v,p);
}
}
signed main() {
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int u,v;
scanf("%d%d",&u,&v);
link(u,v);
link(v,u);
}
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0);
for(int i=1;i<=n;++i) if(!bel[i]) ++edcccnt,build(i);
for(int i=1;i<=n;++i) {
for(int j=head[i];j;j=edge[j].lst) {
if(bel[i]==bel[edge[j].des]) continue;
g[bel[i]].push_back(bel[edge[j].des]);
}
}
dfs(1,0);
printf("%d\n",(leaf+1)/2);
return 0;
}
II. [洛谷3469] - BLO-Blockade
思路分析
简单数数题,考虑对于每一个割点考虑,如果某个点 \(u\) 不是割点,那么答案只可能是点 \(u\) 与其他某个点断连,故答案为 \(2(n-1)\)
如果某个点 \(u\) 是一个割点,那么考虑切断所有与 \(u\) 相连的边,得到若干个连通块,它们的大小分别为 \(siz_1\sim siz_m\),则其答案为:
\]
回顾割点的求法搜索树上 \(u\) 的满足 \(low_v\ge dfn_u\) 的子节点 \(v\) 的子树成为一个连通块,\(u\) 本身和搜索树上不在满足的其他点构成一个连通块
代码呈现
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+1;
vector <int> edge[MAXN];
int dfn[MAXN],low[MAXN],dfncnt,siz[MAXN],ans[MAXN],n,m;
bool cut[MAXN];
inline void tarjan(int p,int lim) {
dfn[p]=low[p]=++dfncnt;
siz[p]=1;
int cnt=0,sum=0;
for(int v:edge[p]) {
if(!dfn[v]) {
tarjan(v,1);
siz[p]+=siz[v];
low[p]=min(low[p],low[v]);
if(low[v]>=dfn[p]) {
++cnt;
ans[p]+=(n-siz[v])*siz[v];
sum+=siz[v];
if(cnt>=lim) cut[p]=true;
}
} else low[p]=min(low[p],dfn[v]);
}
if(!cut[p]) ans[p]=2*(n-1);
else ans[p]+=(n-1)+(n-sum-1)*(sum+1);
}
signed main() {
scanf("%lld%lld",&n,&m);
for(int i=1;i<=m;++i) {
int u,v;
scanf("%lld%lld",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
}
tarjan(1,2);
for(int i=1;i<=n;++i) printf("%lld\n",ans[i]);
return 0;
}
III. [洛谷3627] - 抢掠计划
思路分析
首先对于每个 SCC 进行缩点,然后在缩点后的 DAG 上用 SPFA 跑全源最长路即可
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+1;
struct node {
int des,val;
};
vector <node> edge[MAXN],g[MAXN];
int dfn[MAXN],low[MAXN],dfncnt,st[MAXN],top,scccnt,bel[MAXN],w[MAXN],val[MAXN],dis[MAXN];
bool ins[MAXN],ist[MAXN],inq[MAXN];
inline void tarjan(int p) {
dfn[p]=low[p]=++dfncnt;
st[++top]=p;
ins[p]=true;
for(auto e:edge[p]) {
int v=e.des;
if(!dfn[v]) {
tarjan(v);
low[p]=min(low[v],low[p]);
} else if(ins[v]) low[p]=min(low[p],low[v]);
}
if(low[p]==dfn[p]) {
++scccnt;
int k;
do {
k=st[top--];
ins[k]=false;
bel[k]=scccnt;
val[scccnt]+=w[k];
} while(k!=p);
}
}
signed main() {
int n,m,s,p;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int u,v;
scanf("%d%d",&u,&v);
edge[u].push_back((node){v,0});
}
for(int i=1;i<=n;++i) scanf("%d",&w[i]);
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;++i) {
for(auto e:edge[i]) {
if(bel[i]==bel[e.des]) continue;
g[bel[i]].push_back((node){bel[e.des],val[bel[e.des]]});
}
}
scanf("%d%d",&s,&p);
for(int i=1;i<=p;++i) {
int x;
scanf("%d",&x);
ist[x]=true;
}
queue <int> q;
memset(dis,-0x3f,sizeof(dis));
q.push(bel[s]);
dis[bel[s]]=val[bel[s]];
inq[bel[s]]=true;
while(!q.empty()) {
int p=q.front();q.pop();
inq[p]=false;
for(auto e:g[p]) {
int v=e.des;
if(dis[v]<dis[p]+e.val) {
dis[v]=dis[p]+e.val;
if(!inq[v]) {
q.push(v);
inq[v]=true;
}
}
}
}
int res=0;
for(int i=1;i<=n;++i) if(ist[i]) res=max(res,dis[bel[i]]);
printf("%d\n",res);
return 0;
}
IV. [洛谷3119] - Grass Cownoisseur
思路分析
跟上一题相似,对 SCC 缩点,为了解决一次逆向行走的限制,我们可以在分层图上求解,第一层的图表示没有逆行,第二层的图表示逆行之后,对于原图中的一条有向边 \(u\to v\),我们可以连接第一层的 \(v\) 和第二层的 \(u\),然后再在分层图上 SPFA 计算最长路即可
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+1;
struct node {
int des,val;
};
vector <node> edge[MAXN],g[MAXN<<1];
int dfn[MAXN],low[MAXN],dfncnt,st[MAXN],top,scccnt,bel[MAXN],val[MAXN],dis[MAXN<<1];
bool ins[MAXN],inq[MAXN<<1];
inline void tarjan(int p) {
dfn[p]=low[p]=++dfncnt;
st[++top]=p;
ins[p]=true;
for(auto e:edge[p]) {
int v=e.des;
if(!dfn[v]) {
tarjan(v);
low[p]=min(low[v],low[p]);
} else if(ins[v]) low[p]=min(low[p],low[v]);
}
if(low[p]==dfn[p]) {
++scccnt;
int k;
do {
k=st[top--];
ins[k]=false;
bel[k]=scccnt;
++val[scccnt];
} while(k!=p);
}
}
signed main() {
int n,m,s=1;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int u,v;
scanf("%d%d",&u,&v);
edge[u].push_back((node){v,0});
}
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;++i) {
for(auto e:edge[i]) {
if(bel[i]==bel[e.des]) continue;
g[bel[i]].push_back((node){bel[e.des],val[bel[i]]});
g[bel[i]+scccnt].push_back((node){bel[e.des]+scccnt,val[bel[i]]});
g[bel[e.des]].push_back((node){bel[i]+scccnt,val[bel[e.des]]});
}
}
queue <int> q;
memset(dis,0,sizeof(dis));
q.push(bel[s]);
dis[bel[s]]=0;
inq[bel[s]]=true;
while(!q.empty()) {
int p=q.front();q.pop();
inq[p]=false;
for(auto e:g[p]) {
int v=e.des;
if(dis[v]<dis[p]+e.val) {
dis[v]=dis[p]+e.val;
if(!inq[v]) {
q.push(v);
inq[v]=true;
}
}
}
}
printf("%d\n",max(dis[bel[s]+scccnt],dis[bel[s]]));
return 0;
}
V. [洛谷2515] - 软件安装
思路分析
一道 tarjan 和树形 dp 的复合题,考虑对于每个点 \(i\),将 \(d_i\) 向 \(i\) 连一条边之后,原图会形成一个基环外向树森林,由于一个形成环的依赖关系必须同时全选,考虑对于每个基环树的环缩成一个点,然后建一个虚拟根节点连向所有入度为 \(0\) 的 SCC,然后在树上做一遍简单背包即可
树上依赖性背包大概和选课差不多
时间复杂度 \(\Theta(nm^2)\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=101,MAXM=501,INF=1e18;
int val[MAXN],wgh[MAXN],d[MAXN],deg[MAXN],n,m,res;
int inv[MAXN],inw[MAXN];
int dp[MAXN][MAXM];
vector <int> edge[MAXN],g[MAXN];
inline void dfs(int p) {
if(wgh[p]<=m) dp[p][wgh[p]]=val[p];
for(int v:g[p]) {
dfs(v);
for(int i=m;i>=0;--i) {
for(int j=i;j>=0;--j) {
dp[p][i]=max(dp[p][i],dp[v][j]+dp[p][i-j]);
}
}
}
dp[p][0]=0;
}
int dfn[MAXN],low[MAXN],dfncnt,st[MAXN],top,bel[MAXN],scccnt;
bool ins[MAXN];
inline void tarjan(int p) {
dfn[p]=low[p]=++dfncnt;
st[++top]=p;
ins[p]=true;
for(int v:edge[p]) {
if(!dfn[v]) {
tarjan(v);
low[p]=min(low[v],low[p]);
} else if(ins[v]) low[p]=min(low[p],low[v]);
}
if(dfn[p]==low[p]) {
++scccnt;
int k;
do {
k=st[top--];
ins[k]=false;
bel[k]=scccnt;
wgh[scccnt]+=inw[k];
val[scccnt]+=inv[k];
} while(k!=p);
}
}
signed main() {
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i) scanf("%lld",&inw[i]);
for(int i=1;i<=n;++i) scanf("%lld",&inv[i]);
for(int i=1;i<=n;++i) {
scanf("%lld",&d[i]);
if(d[i]) edge[d[i]].push_back(i);
}
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;++i) {
for(int j:edge[i]) {
if(bel[i]==bel[j]) continue;
g[bel[i]].push_back(bel[j]);
++deg[bel[j]];
}
}
for(int i=1;i<=scccnt;++i) if(!deg[i]) g[0].push_back(i);
memset(dp,-0x3f,sizeof(dp));
dfs(0);
for(int i=0;i<=m;++i) res=max(res,dp[0][i]);
printf("%lld\n",res);
return 0;
}
VI. [洛谷4334] - Policijia
思路分析
tarjan 好题,考虑对于原图建立出 dfs 树并预处理 \(dfn\) 和 \(low\) 数组,在 dfs 树上解决问题,注意 \(low_u\) 不能经过 \(u\) 的父亲
- 删边操作
考虑删除边 \((u,v)\) 后使 \(a,b\) 连通的条件,如果 \((u,v)\) 是非树边(返祖边),一定对答案无影响,故假设 \((u,v)\) 是树边,且 \(u\) 是 \(v\) 的父亲
- \(a,b\) 都在 \(v\) 的子树中
- \(a,b\) 都不在 \(v\) 的子树中
- \(a,b\) 有且仅有一个在 \(v\) 的子树中,且 \((u,v)\) 不为桥
根据 dfn 序和桥的判定解决即可
- 删点操作
考虑删除点 \(c\) 后,\(a,b\) 所在的 \(c\) 的某棵子树(如果在的话)是否与外界不连通
由于 \(a,b\) 所在的子树中的位置对于答案没有影响,所以如果 \(a,b\) 在 \(c\) 的子树中,我们就用 \(x,y\) 来表示 \(c\) 的儿子中子树包含 \(a,b\) 的节点
那么删除 \(c\) 后,\(a,b\) 依然联通的可能条件如下
- \(a,b\) 均不在 \(c\) 的子树中
- 仅有 \(a\) 在 \(c\) 的子树中,且删去 \(c\),\(x\) 依然与外界联通,仅有 \(b\) 同理
- \(a,b\) 均在 \(c\) 的子树中,且删去 \(c\),\(x,y\) 依然均与外界联通
通过维护每个节点在 dfs 树上的深度并且结合倍增,可以在 \(\Theta(\log n)\) 的时间内求出 \(x,y\)
然后用割点的性质判定即可
时间复杂度 \(\Theta\left( (n+q)\log n\right )\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+1;
int low[MAXN],dfn[MAXN],dep[MAXN],lid[MAXN],rid[MAXN],dfncnt,fa[MAXN][21];
vector <int> edge[MAXN];
inline void tarjan(int p,int f) {
dep[p]=dep[f]+1;
low[p]=dfn[p]=lid[p]=++dfncnt;
fa[p][0]=f;
for(int i=1;i<=20;++i) fa[p][i]=fa[fa[p][i-1]][i-1];
for(int v:edge[p]) {
if(v==f) continue;
if(!dfn[v]) {
tarjan(v,p);
low[p]=min(low[p],low[v]);
} else low[p]=min(low[p],dfn[v]);
}
rid[p]=dfncnt;
}
inline int jump(int u,int d) {
for(int i=20;i>=0;--i) {
if(d>=(1<<i)) {
u=fa[u][i];
d-=(1<<i);
}
}
return u;
}
inline bool subtree(int x,int r) {
return lid[r]<=lid[x]&&rid[x]<=rid[r];
}
inline bool CutEdge(int x,int y,int a,int b) {
if(dep[x]<dep[y]) swap(x,y);
if(fa[x][0]!=y) return false;
if(subtree(a,x)==subtree(b,x)) return false;
return low[x]>dfn[y];
}
inline bool CutNode(int x,int a,int b) {
if((!subtree(a,x))&&(!subtree(b,x))) return false;
if(subtree(a,x)&&subtree(b,x)) {
a=jump(a,dep[a]-dep[x]-1);
b=jump(b,dep[b]-dep[x]-1);
if(a==b) return false;
return low[a]>=dfn[x]||low[b]>=dfn[x];
} else {
if(subtree(a,x)) {
a=jump(a,dep[a]-dep[x]-1);
return low[a]>=dfn[x];
} else {
b=jump(b,dep[b]-dep[x]-1);
return low[b]>=dfn[x];
}
}
}
signed main() {
int n,m,q;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int u,v;
scanf("%d%d",&u,&v);
edge[u].push_back(v);
edge[v].push_back(u);
}
tarjan(1,1);
scanf("%d",&q);
while(q--) {
int opt;
scanf("%d",&opt);
if(opt==1) {
int x,y,a,b;
scanf("%d%d%d%d",&a,&b,&x,&y);
puts(CutEdge(x,y,a,b)?"no":"yes");
}
if(opt==2) {
int x,a,b;
scanf("%d%d%d",&a,&b,&x);
puts(CutNode(x,a,b)?"no":"yes");
}
}
return 0;
}
VII. [洛谷5234] - 越狱老虎桥
思路分析
显然,任何一条不是桥的边都不会对答案造成影响(因为在一个 E-DCC 中,任意删去一条边都不可能使图不连通)
所以我们可以对原图建立 dfs 搜索树并且求出桥,将所有树上非桥的边的边权都设为 \(+\infty\)
假设连了某一条边 \((u,v)\) ,使得答案为 \(k\),则所有边权 \(<k\) 的边都应该在简单路径 \((u,v)\) 上
考虑对答案二分,如果需要检查某个 \(k\) 是否可能成为答案,我们只需要找到一条路径 \((u,v)\) 覆盖所有边权 \(<k\) 的边即可
因此我们可以对每条边权 \(<k\) 的边设为 \(1\) 否则设为 \(0\),然后用这个边权求一遍树的直径,只需要检查直径长度是否等于边权 \(<k\) 的边的数量即可
时间复杂度 \(\Theta(n\log T)\)
代码呈现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+1,INF=1e9;
struct node {
int des,val,lst;
} edge[MAXN<<1],tr[MAXN<<1];
int low[MAXN],dfn[MAXN],head1[MAXN],head2[MAXN],cnt[MAXN],dp[MAXN],tot=0,ans=0,dfncnt,totedge=1,tottree=0,n,m;
inline void addedge(int u,int v,int w) {
edge[++totedge]=(node){v,w,head1[u]};
head1[u]=totedge;
}
inline void addtree(int u,int v,int w) {
tr[++tottree]=(node){v,w,head2[u]};
head2[u]=tottree;
}
inline void tarjan(int p,int uid) {
low[p]=dfn[p]=++dfncnt;
for(int i=head1[p];i;i=edge[i].lst) {
int v=edge[i].des;
if(!dfn[v]) {
tarjan(v,i);
low[p]=min(low[p],low[v]);
if(low[v]<=dfn[p]) addtree(p,v,INF);
else addtree(p,v,edge[i].val);
} else if(i!=(uid^1)) low[p]=min(low[p],dfn[v]);
}
return ;
}
inline void dfs(int p,int l) {
vector <int> vec;
if(!head2[p]) dp[p]=cnt[p];
for(int i=head2[p];i;i=tr[i].lst) {
int v=tr[i].des;
cnt[v]=cnt[p];
if(tr[i].val<l) ++cnt[v],++tot;
dfs(v,l);
vec.push_back(dp[v]);
}
sort(vec.begin(),vec.end(),greater<int>());
if(vec.size()>0) dp[p]=vec[0],ans=max(vec[0]-cnt[p],ans);
if(vec.size()>1) ans=max(ans,vec[0]+vec[1]-cnt[p]*2);
}
inline bool check(int x) {
memset(cnt,0,sizeof(cnt));
memset(dp,0,sizeof(dp));
ans=tot=0;
dfs(1,x);
return ans==tot;
}
signed main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i) {
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
addedge(u,v,w);
addedge(v,u,w);
}
tarjan(1,0);
int l=0,r=INF,res=-1;
while(l<=r) {
int mid=(l+r)>>1;
if(check(mid)) l=mid+1,res=mid;
else r=mid-1;
}
if(res==INF) res=-1;
printf("%d\n",res);
return 0;
}