\(\text{By DaiRuiChen007}\)

一、KMP 算法

I. 问题描述

在文本串 \(S\) 中找到模式串 \(T\) 的所有出现，其中 \(|S|=n,|T|=m\)

II. 前置定义

记 \(\pi_i\) 表示 \(\max\{j|j<i\land T[1\cdots j]=T[i-j+1\cdots j]\}\)，即 \(T[1\cdots i]\) 最长 Border 的长度

III. 算法实现

假设我们已经知道了 \(\{\pi_i\}\)，我们能够写出如下的匹配伪代码：

i=j=0
while i<n:
	if S[i+1]=T[i+1]:
		i=i+1,j=j+1
		if j=m:
			print i-m+1
			j=pi[j]
	else:
		if j>0:
			j=pi[j]
		else:
			i=i+1

我们可以证明 \(i\) 至多右移 \(|S|\) 次且不会左移，而 \(j\) 也至多右移 \(|S|\) 次，且 \(j\gets \pi_j\) 的时候至少会让 \(j\) 左移 \(1\)，因此左移次数不超过又移次数，所以整个匹配过程的复杂度是 \(\Theta(|S|)\)

为了求出 \(\{p_i\}\)，我们有如下的伪代码：

i=1,j=0,pi[1]=0
while i<n:
	if T[i+1]=T[j+1]:
		i=i+1,j=j+1
		pi[i]=j
	else:
		if j>0:
			j=pi[j]
		else:
			pi[i]=0
			i=i+1

类似上面的分析，我们知道求 \(\{p_i\}\) 的复杂度是 \(\Theta(|T|)\) 的，因此整个 KMP 算法的复杂度是 \(\Theta(|S|+|T|)\) 的

IV. 算法应用

循环同构

对于两个字符串 \(S,T\) 满足 \(|S|=|T|=n\)，如果存在一个 \(i\) 使得 \(S=T[\delta\cdots n-1]+T[0\cdots \delta-1]\)，那么称 \(S\) 与 \(T\) 循环同构，一般认为 \(0<\delta<n\)

我们可以把 \(S\) 和 \(T\) 都看成同一个环上从不同位置出发形成的两个不同的字符串，因此判断循环同构可以对 \(S\) 破环为链，然后在 \(S+S\) 中匹配 \(T\) 即可

Border 集合

为了表示方便，我们简记 \(\pi_{\pi_i}=\pi^{(2)}_i\)，\(\pi^{(k)}=\pi_{\pi^{(k-1)}_i}\)，即迭代 \(k\) 次后的结果

对于 \(T[1\cdots i]\)，其所有的 Border 构成的集合 \(Border_i=\{\pi_i,\pi^{(2)}_i,\pi^{(3)}_i,\cdots\}\)

证明：

考虑对 \(i\) 进行数学归纳法，假设对于所有 \(<i\) 的 \(j\)，该命题都成立

我们知道 \(Border_{pi_i}\subseteq Border_i\)，且 \(Border_i=\pi_i+Border_{\pi_i}\)，我们只需要证明长度在 \((\pi^{(2)}_i,\pi_i)\) 之间的 Border 不存在即可，这一步的证明比较简单，通过假设其存在导出有关 \(\pi^{(2)}_i=\pi_{\pi_i}\) 的矛盾即可

失配树

把所有 \(i\) 向 \(\pi_i\) 连边能够得到一棵树，其中每个 \(\pi_i\) 为 \(i\) 的父亲，根节点为 \(0\)，此时 \(i\) 到根的路径恰好对应 \(Border_i\)

VI. 周期问题

周期问题

定义一个字符串 \(S\) 的某个周期 \(P\) 为满足 \(P\in(0,|S|),\forall i\in[1,|S|-P]:S_i=S_{i+p}\) 的整数

特别地，假如某个 \(P\) 满足 \(|S|\bmod P=0\)，那么称 \(S\) 为 \(P\) 的一个整周期，设 \(A=S[0\cdots p-1]\)，那么存在一个整数 \(d\) 使得 \(S=\underbrace{A+A+\cdots +A}_{d \text{ times}}\)，一般简记为 \(S=A^d\)

我们有结论，\(P=n-\pi^{(k)}_n\)，其中 \(\pi^{(k)}_{n}>0\)

证明：

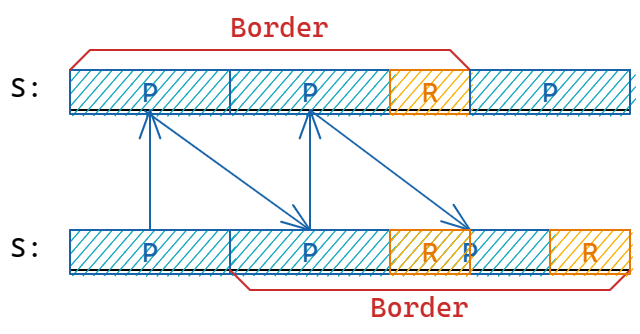
实际上只需要证明：\(P\) 为 \(S\) 的周期等价于 \(S[1\cdots |S|-P]\) 为 \(S\) 的一个 Border

简要的证明如下图：

周期问题与循环同构

命题

定义两个字符串 \(A,B\)，记 \(R(S)=S^\infty=S+S+S+\cdots\)，有结论 \(R(A)=R(B)\iff A+B=B+A\)

思路

构造一个中间命题：观察发现如果满足 \(R(A)=R(B)\) 或 \(A+B=B+A\)，我们都能将 \(A,B\) 分别表示成 \(X^i,X^j\) 的形式，因此我们要证明的命题变成了：\(R(A)=R(B)\iff \exists X:A=X^i,B=X^j\iff A+B=B+A\)

注意到 \(\exists X:A=X^i,B=X^j\implies R(A)=R(B)\)，\(\exists X:A=X^i,B=X^j\implies A+B=B+A\) 都是显然的，因此只需要证明剩下的两个方向即可

引理

对于任意一个字符串 \(S\)，假如 \(S\) 有整周期 \(a,b\)，那么 \(S\) 必然会有整周期 \(g=\gcd(a,b)\)，证明如下：

证：

对于字符串下标我们在 \(\bmod |S|\) 意义下讨论

由于裴蜀定理，存在一组整数 \((x,y)\) 使得 \(ax+by=g\)，那么我们能得到如下结论：

\[\begin{aligned}
S_{i+g}&=S_{i+ax+by}\\
&=S_{(i+ax+by)\bmod b}\\
&=S_{i+ax}\\
&=S_{(i+ax)\bmod a}\\
&=S_i
\end{aligned}
\]

且 \(g\mid a,a\mid n\)，所以 \(g\mid n\)

所以字符串 \(S\) 有整周期 \(g\)

子问题一

下证 \(R(A)=R(B)\implies \exists X:A=X^i,B=X^j\)：

证：

假设 \(a=|A|,b=|B|\)

由于 \(R(A)=R(B)\)，因此 \(A^b=R(A)[1\cdots a\times b]=R(B)[1\cdots a\times b]=B^a\)

不妨记 \(A^b=C=B^a\)，由于 \(C\) 有整周期 \(a,b\)，那么根据引理，\(C\) 有整周期 \(g=\gcd(a,b)\)，记 \(X=C[1\cdots g]\)

此时 \(A=X^{b/g},B=X^{a/g}\)，由于 \(g\mid a,g\mid b\)，因此 \(A,B\) 有公共整周期 \(C[1\cdots g]\)，故原命题得证

子问题二

\(A+B=B+A\implies \exists X:A=X^i,B=X^j\) 证明如下：

设 \(|A|\ge |B|\)：

\(|A|=|B|\)：

此时 \(A=B\)，构造 \(X=A,i=1,j=1\) 的情况即可

\(|A|>|B|\)

此时 \(A+B\) 中 \(A[1\cdots b]=B[1\cdots b]\)，考虑剩下的一个子段 \(A[b+1\cdots a]\) 有 \(A[b+1\cdots a]=B[1\cdots a-b]\)，考虑这个子段 \(C\)，那么根据上面的分析我们也能知道 \(A[b+1\cdots a]=C=B[1\cdots a-b]=A[1\cdots a-b]\)，所以有 \(B+C=A=C+B\)，那么递归对于 \(B,C\) 构造合法的一组 \(B=X^{i'},C=X^{j'}\)，也能得到 \(A=X^{i'+j’}，B=X^{j'}\)，那么根据类似辗转相除法的递归过程能够证明该命题

综上所述，\(R(A)=R(B)\iff A+B=B+A\)

整周期问题

问题描述

对于字符串 \(S\) 若可以写成 \(S=A^d\)，其中 \(A\) 为字符串，\(d\) 为一个正整数，对于所有这样的 \(A,d\)，其中 \(|A|\) 最小的 \(A\) 被记为 \(root(S)\)

结论

记 \(r=|root(S)|,n=|S|\)，那么有如下结论：

\[r=
\begin{cases}
n-\pi_n&n-\pi_n\mid n\\
n&\text{otherwise}
\end{cases}
\]

引理一

在这里设 \(S\) 的下标从 \(0\) 开始标号

如果 \(S\) 的某个循环同构串 \(S'\) 有 \(S'=S\)，那么这事实上等价于 \(r<n\)

显然在 \(r<n\) 的时候令位移量 \(\delta =r\) 即可得到两个循环同构的字符串因此右推左是显然的

此时假设 \(S[0\cdots n-1]=S[\delta\cdots n-1]+S[0\cdots \delta-1]\)，我们需要证明 \(|root(S)|<n\)，即找到一个非平凡的整周期

假设下标在 \(\bmod n\) 意义下，对于所有 \(i\) 都有 \(S_i=S_{i+\delta}\)，且 \(S_i=S_{i+n}\)

所以我们证明了 \(R(S)\) 有两个整周期 \(\delta\) 和 \(n\)，根据在上一个问题中的结论，\(R(S)\) 有一个大小为 \(g=\gcd(\delta,n)\) 的整周期，又因为 \(g\mid n\)，因此 \(S[0\cdots g-1]\) 同样是 \(S\) 的整周期且 \(\delta <n\)，因此 \(r\le g<n\)，原命题得证

引理二

\(r<n\implies r\le n-\pi_n\)

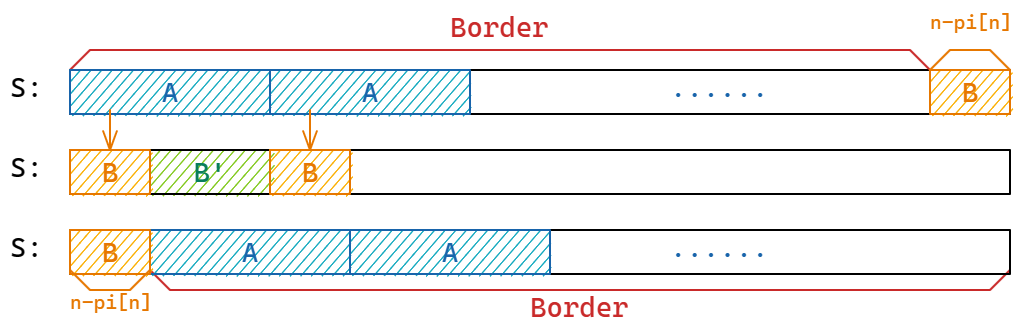
采取反证法，假设 \(n-\pi_n<r<n\)，那么如同下图的操作，我们设 \(B=S[1,\cdots n-\pi_n]\)，那么根据假设 \(B=A[1\cdots n-\pi_n]\)，不妨设 \(B'=A[n-\pi_n+1\cdots r]\)

那么我们得到：\(B+B'=S[1\cdots n-\pi_n]+S[n-\pi_n+1\cdots r]=S[1\cdots r]=A\)

又因为 \(S[1\cdots r]=A=S[r+1\cdots 2\times r]\)，所以 \(S[r+1,\cdots n-\pi_n+r]=B\)

又因为 Border 的定义，\(S[n-\pi_n+1\cdots n]=S[1\cdots \pi_n]\)，那么 \(S[n-\pi_n+1\cdots n-\pi_n+r]=S[1\cdots r]=A\)

且 \(S[n-\pi_n+1\cdots n-\pi_n+r]=S[n-\pi_n+1\cdots r]+S[r+1\cdots n-\pi_n+r]=B'+B\)

所以根据上面的分析，我们构造出了两个字符串 \(B,B'\) 使得 \(B+B'=B'+B\)，此时令位移量 \(\delta=n-\pi_n\)，我们就得到了一个 \(A\) 的循环同构串，那么根据引理一，我们有 \(|root(A)|<A\)，不过这与 \(A\) 是 \(S\) 所有整周期中最小的一个矛盾，故当 \(r<n\) 时，一定有 \(r\le n-\pi_n\)

证明

根据整周期的定义，我们知道 \(S[1\cdots n-r]\) 是 \(S\) 的一个 Border，结合 \(\pi_n\) 的定义有 \(\pi_n\ge n-r\)，变形得到 \(r\ge n-\pi_n\)

当 \(n-\pi_n\mid n\) 时：

我们知道 \(S[1\cdots n-\pi_n]\) 是 \(S\) 的一个周期，又因为 \(n-\pi_n\mid S\)，我们得到 \(S[1\cdots n-\pi_n]\) 是 \(S\) 的一个整周期

根据 \(r=root(S)\) 这一定义，我们得到 \(r\le n-\pi_n\)
- 当 \(\pi_n=0\) 时：显然 \(r=n=n-\pi_n\) 命题成立
- 当 \(\pi_n>0\) 时：\(r\le n-\pi_n<n\)，根据引理二 \(r\le n-\pi_n\)，与 \(r\ge n-\pi_n\) 结合得到 \(r=n-\pi_n\)
因此我们证明了在 \(n-\pi_n\mid n\) 时 \(r=n-\pi_n\)
当 \(n-\pi_n\nmid n\) 时：

若 \(r<n\)，则类似上面的过程我们得到 \(r=n-\pi_n\)，不过根据整周期的定义，\(S[1\cdots r]\) 不会作为 \(S\) 的整周期，因此 \(r\) 一定 \(=n\)

综上所述，我们证明了：

\[|root(S)|=
\begin{cases}
n-\pi_n&n-\pi_n\mid n\\
n&\text{otherwise}
\end{cases}
\]

VII. 习题演练

[BZOJ1511] - Periods of Words

Problem Link

根据题目中的定义，我们要找到的周期 \(P\) 满足 \(P\in \left[\dfrac{|A|}2,|A|\right)\)，而根据周期的定义，我们要找到 \(A\) 中长度 \(\le\dfrac{|A|}2\) 的最小 Border，用并查集维护失配树，把 \(\pi_i=0\) 的 \(i\) 当成新的根即可找到每个前缀的最小 Border

事实上我们有如下的观察：

观察：定义 \(\pi^\star\) 表示 \(S\) 的最短 Border的长度，则一定有 \(2\times \pi^\star\le |S|\)

证明：采用反证法，若 \(2\times \pi^\star> |S|\)，则前后缀必然有相交的子段，这个相交的子段是 \(S[1\cdots \pi^\star]\) 的 Border，也是 \(S\) 一个更小的 Border，矛盾

所以我们只需要判断每个 \(S[1\cdots i]\) 的 Border 长度是否 \(=i\) 即可

时间复杂度 \(\Theta(|S|\alpha(|S|))\)，\(\alpha\) 为反阿克曼函数

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+1;
char ch[MAXN];
int kmp[MAXN];
inline int find(int x) {
	if(kmp[x]==0) return x;
	return kmp[x]=find(kmp[x]);
}
signed main() {
	int n,ans=0;
	scanf("%lld%s",&n,ch+1);
	for(int i=2,j=0;i<=n;++i) {
		while(j!=0&&ch[j+1]!=ch[i]) j=kmp[j];
		if(ch[j+1]==ch[i]) ++j;
		kmp[i]=j;
	}
	for(int i=1;i<=n;++i) {
		int k=find(i);
		if(k!=0) ans+=i-k;
	}
	printf("%lld\n",ans);
	return 0;
}

[洛谷5829] - 【模板】失配树

Problem Link

建出失配树求 LCA 即可，注意根节点为 \(0\)

时间复杂度 \(\Theta((|S|+m)\log|S|)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+1;
char s[MAXN];
int fa[MAXN],dep[MAXN],siz[MAXN],son[MAXN],root[MAXN];
vector <int> G[MAXN];
inline void dfs1(int p,int f) {
	dep[p]=dep[f]+1,siz[p]=1;
	for(int v:G[p]) {
		dfs1(v,p);
		siz[p]+=siz[v];
		if(siz[v]>siz[son[p]]) son[p]=v;
	}
}
inline void dfs2(int p,int r) {
	root[p]=r;
	if(son[p]!=-1) dfs2(son[p],r);
	for(int v:G[p]) if(v!=son[p]) dfs2(v,v);
}
inline int LCA(int u,int v) {
	while(root[u]!=root[v]) {
		if(dep[root[u]]<dep[root[v]]) swap(u,v);
		u=fa[root[u]];
	}
	return dep[u]>dep[v]?v:u;
}
signed main() {
	memset(son,-1,sizeof(son));
	scanf("%s",s+1);
	int n=strlen(s+1);
	G[0].push_back(1);
	for(int i=2,j=0;i<=n;++i) {
		while(j!=0&&s[j+1]!=s[i]) j=fa[j];
		if(s[j+1]==s[i]) ++j;
		fa[i]=j,G[j].push_back(i);
	}
	dfs1(0,0),dfs2(0,0);
	int q;
	scanf("%d",&q);
	while(q--) {
		int u,v;
		scanf("%d%d",&u,&v);
		int k=LCA(u,v);
		if(k==u||k==v) k=fa[k];
		printf("%d\n",k);
	}
	return 0;
}

[CodeForces126B] - Password

Problem Link

可以证明答案除了是 \(S\) 的 Border，同样是 \(S\) 某个真前缀的 Border，也能证明一定是 \(S\) 某个真前缀的最长 Border

因此标记 \(\pi_1\sim \pi_{|S|-1}\) 然后从大到小枚举 \(S\) 的每个 Border 是否被标记过即可

时间复杂度 \(\Theta(|S|)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+1;
int kmp[MAXN];
char s[MAXN];
bool vis[MAXN];
signed main() {
	scanf("%s",s+1);
	int n=strlen(s+1);
	for(int j=0,i=2;i<=n;++i) {
		while(j!=0&&s[j+1]!=s[i]) j=kmp[j];
		if(s[j+1]==s[i]) ++j;
		kmp[i]=j;
	}
	for(int i=1;i<n;++i) vis[kmp[i]]=true;
	for(int i=kmp[n];i;i=kmp[i]) {
		if(vis[i]) {
			for(int j=1;j<=i;++j) printf("%c",s[j]);
			puts("");
			return 0;
		}
	}
	puts("Just a legend");
	return 0;
}

[CodeForces432D] - Prefixes and Suffixes

Problem Link

建立失配树，根据我们刚才的分析得到，\(S[1\cdots i]\) 在 \(S\) 中的出现次数就是 \(i\) 在失配树上的子树大小，因此预处理即可

时间复杂度 \(\Theta(|S|)\)

#include<bits/stdc++.h>
#define pii pair<int,int>
using namespace std;
const int MAXN=1e5+1;
char s[MAXN];
int fa[MAXN],siz[MAXN];
vector <int> G[MAXN];
inline void dfs(int p,int f) {
	siz[p]=1;
	for(int v:G[p]) {
		dfs(v,p);
		siz[p]+=siz[v];
	}
}
signed main() {
	scanf("%s",s+1);
	int n=strlen(s+1);
	G[0].push_back(1);
	for(int i=2,j=0;i<=n;++i) {
		while(j!=0&&s[j+1]!=s[i]) j=fa[j];
		if(s[j+1]==s[i]) ++j;
		fa[i]=j,G[j].push_back(i);
	}
	dfs(0,0);
	vector <int> ans;
	for(int i=n;i;i=fa[i]) ans.push_back(i);
	reverse(ans.begin(),ans.end());
	printf("%d\n",(int)ans.size());
	for(int i:ans) printf("%d %d\n",i,siz[i]);
	return 0;
}

[POJ2406] - Power Strings

Problem Link

最小整周期模板

时间复杂度 \(\Theta(|S|)\)

#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN=1e6+1;
char s[MAXN];
int kmp[MAXN];
signed main() {
	while(scanf("%s",s+1)!=EOF) {
		if(s[1]=='.') break;
		int n=strlen(s+1);
		for(int i=2,j=0;i<=n;++i) {
			while(j!=0&&s[j+1]!=s[i]) j=kmp[j];
			if(s[j+1]==s[i]) ++j;
			kmp[i]=j;
		}
		printf("%d\n",(n%(n-kmp[n])==0)?n/(n-kmp[n]):1);
	}
	return 0;
}

[POJ1961] - Period

Problem Link

同样的最小整周期模板问题

时间复杂度 \(\Theta(|S|)\)

#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN=1e6+1;
char s[MAXN];
int kmp[MAXN];
signed main() {
	for(int t=1;;++t) {
		int n;
		scanf("%d",&n);
		if(!n) break;
		scanf("%s",s+1);
		for(int i=2,j=0;i<=n;++i) {
			while(j!=0&&s[j+1]!=s[i]) j=kmp[j];
			if(s[j+1]==s[i]) ++j;
			kmp[i]=j;
		}
		printf("Test case #%d\n",t);
		for(int i=1;i<=n;++i) {
			if(kmp[i]>0&&i%(i-kmp[i])==0) {
				printf("%d %d\n",i,i/(i-kmp[i]));
			}
		}
		puts("");
	}
	return 0;
}

[CodeForces471D] - MUH and Cube Walls

Problem Link

对差分数组进行 kmp 匹配即可，特判 \(w=1\) 的情况

时间复杂度 \(\Theta(n+w)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+1;
int S[MAXN],T[MAXN],kmp[MAXN];
signed main() {
	int n,m,ans=0;
	scanf("%d%d",&n,&m); --n,--m;
	for(int i=0;i<=n;++i) scanf("%d",&S[i]);
	for(int i=0;i<=m;++i) scanf("%d",&T[i]);
	if(m==0) {
		printf("%d\n",n+1);
		return 0;
	}
	for(int i=n;i>=1;--i) S[i]-=S[i-1];
	for(int i=m;i>=1;--i) T[i]-=T[i-1];
	for(int i=2,j=0;i<=m;++i) {
		while(j!=0&&T[j+1]!=T[i]) j=kmp[j];
		if(T[j+1]==T[i]) ++j;
		kmp[i]=j;
	}
	for(int i=1,j=0;i<=n;++i) {
		while(j!=0&&T[j+1]!=S[i]) j=kmp[j];
		if(T[j+1]==S[i]) ++j;
		if(j==m) ++ans,j=kmp[j];
	}
	printf("%d\n",ans);
	return 0;
}

二、Z 函数

I. 问题描述

\(S\) 下标从 \(0\) 开始标号到 \(|S|-1\)，记 \(n=|S|\)

求出 \(S\) 的每个后缀 \(S[i\cdots n]\) 与 \(S\) 的最长公共前缀

II. 算法实现

我们维护一个 Z-Box，记为 \([l,r]\)，表示 \(S[l\cdots r]\) 为 \(S\) 的前缀，且 \([l,r]\) 为所有满足条件且 \(l<i\) 的区间中 \(r\) 最大的一个

假设当前的 \(i\in [l,r]\)，那么我们匹配 \(S[i\cdots n]\) 和 \(S[0\cdots n]\) 可以先将 \(S[i\cdots n]\) 与 \(S[(i-l)\cdots (r-l)]\) 这一段配对，再将 \(S[(i-l)\cdots (r-l)]\) 与 \(S[0\cdots z_{i-l}]\) 配对，因此我们知道 \(z_i\) 可以先跳到 \(\min(r-i+1,z_{i-l})\) 上，剩下的再暴力移动即可

我们可以写出如下的伪代码：

l=0,r=0,z[0]=n
for i from 1 to n-1:
	if i<=r:
		z[i]=min(z[i-l],r-i+1)
	while z[i]<n and S[i+z[i]]=S[z[i]]:
		z[i]=z[i]+1
	if i+z[i]-1>r:
		l=i,r=i+z[i]-1

注意到每次进入 while 循环更新 \(z_i\) 的时候 \(r\) 也要不断变大，因此 while 循环内部的语句执行次数是 \(\Theta(n)\) 的

因此 Z 函数的总复杂度为 \(\Theta(n)\)

III. 习题演练

[洛谷5410] - 【模板】扩展 KMP（Z 函数）

Problem Link

第一问直接求解，而第二问考虑构造字符串 \(b+\texttt #+a\)，其中 \(\texttt #\) 为任意不在 \(a,b\) 字符集内的字符，求出这个字符串的 Z 函数，我们就能得到 \(a[i\cdots |a|-1]\) 与 \(b\) 的 lcp 长度了

时间复杂度 \(\Theta(|A|+|B|)\)

#include<bits/stdc++.h>
using namespace std;
inline vector<int> Zfunc(string s) {
	int n=s.length();
	vector <int> z(n);
	z[0]=n;
	for(int i=1,l=0,r=0;i<n;++i) {
		if(i<=r) z[i]=min(z[i-l],r-i+1);
		while(i+z[i]<n&&s[i+z[i]]==s[z[i]]) ++z[i];
		if(i+z[i]-1>r) l=i,r=i+z[i]-1;
	}
	return z;
}
signed main() {
	string a,b;
	cin>>a>>b;
	vector <int> Z=Zfunc(b+"#"+a);
	Z[0]=b.length();
	int v1=0,v2=0;
	for(int i=0;i<(int)b.length();++i) v1^=(i+1)*(Z[i]+1);
	for(int i=0;i<(int)a.length();++i) v2^=(i+1)*(Z[b.length()+i+1]+1);
	cout<<v1<<"\n"<<v2<<"\n";
	return 0;
}

[UVAoj11475] - Extend to Palindrome

Problem Link

记 \(|S|=n\)

考虑最坏情况，假设 \(S\) 反转后得到 \(T\)，那么 \(S^\star\) 的长度至多为 \(2|S|\)，因为 \(S+T\) 一定是合法的

此时考虑缩小 \(T\)，显然最终的答案一定是 \(S+T[i\cdots (n-1)]\)，其中 \(T[0\cdots i]\) 是一个回文串，这是根据回文串的基础性质得出的，注意到 \(T[0\cdots i]\) 是回文串等价于 \(S[(n-i-1)\cdots(n-1)]=T[0\cdots i]\)，因此构造字符串 \(T+\texttt #+S\) 求 Z 函数然后求出 \(i+z_i-1=2\times n\) 的最小 \(i\) 即可

时间复杂度 \(\Theta(|S|)\)

#include<bits/stdc++.h>
using namespace std;
inline string rev(string s) {
	reverse(s.begin(),s.end());
	return s;
}
inline vector<int> Zfunc(string s) {
	int n=s.length();
	vector <int> z(n);
	z[0]=n;
	for(int i=1,l=0,r=0;i<=n;++i) {
		if(i<=r) z[i]=min(z[i-l],r-i+1);
		while(i+z[i]<n&&s[i+z[i]]==s[z[i]]) ++z[i];
		if(i+z[i]-1>r) l=i,r=i+z[i]-1;
	}
	return z;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	string s;
	while(cin>>s) {
		int n=s.length();
		string t=rev(s);
		vector <int> z=Zfunc(t+"#"+s);
		for(int i=0;i<n;++i) {
			int p=i+n+1;
			if(p+z[p]-1==2*n) {
				for(int j=0;j<i;++j) cout<<s[j];
				cout<<t<<"\n";
				goto match;
			}
		}
		cout<<s<<t<<"\n";
		match:;
	}
}

[洛谷7114] - 字符串匹配

Problem Link

首先求出 Z 函数，对于一个前缀 \(S[0\cdots i]\)，若 \(AB=S[0\cdots i]\)，那么满足 \(S=(AB)^kC\) 的最大 \(k\) 应该是 \(1\sim \left\lfloor\dfrac{z_{i+1}}{i+1}\right\rfloor+1\)，分别讨论注意到每个 \((AB)^2\) 在不在 \(C\) 中不影响 \(f(C)\)，因此对 \(k\) 为奇数和偶数分别讨论，并记录 \(S[0\cdots0]\sim S[0\cdots i-1]\) 中每个前缀的 \(f\) 值：

若 \(k\) 为奇数，那么 \(f(C)=f(S-AB)\)
若 \(k\) 为偶数，那么 \(f(C)=f(S)\)

因此维护全局 \(f\) 值和每个时刻的前后缀 \(f\) 值，然后对于所有 \(f(S[0\cdots 0])\sim f(S[0\cdots i-1])\) 开桶维护即可

时间复杂度 \(\Theta(|S|\times |\Sigma|)\)，用树状数组维护桶可以优化到 \(\Theta(|S|\log|\Sigma|)\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
bool L[26],R[26];
int cnt[26];
inline vector<int> Zfunc(string s) {
	int n=s.length();
	vector <int> z(n);
	z[0]=n;
	for(int i=1,l=0,r=0;i<n;++i) {
		if(i<=r) z[i]=min(z[i-l],r-i+1);
		while(i+z[i]<n&&s[i+z[i]]==s[z[i]]) ++z[i];
		if(i+z[i]-1>r) l=i,r=i+z[i]-1;
	}
	return z;
}
inline int sum(int t) {
	int ret=0;
	for(int i=0;i<=t;++i) ret+=cnt[i];
	return ret;
}
inline void solve() {
	memset(L,0,sizeof(L)),memset(R,0,sizeof(R));
	memset(cnt,0,sizeof(cnt));
	string s; cin>>s;
	vector <int> z=Zfunc(s);
	int n=s.length(),tot=0,pre=0,suf=0,ans=0;
	for(int i=0;i<n;++i) if(i+z[i]-1==n-1) --z[i];
	for(int i=0;i<n;++i) R[s[i]-'a']^=1;
	for(int i=0;i<26;++i) tot+=R[i],suf+=R[i];
	for(int i=0;i<n;++i) {
		suf=R[s[i]-'a']?suf-1:suf+1,R[s[i]-'a']^=1;
		pre=L[s[i]-'a']?pre-1:pre+1,L[s[i]-'a']^=1;
		if(i==0||i==n-1) {
			++cnt[pre];
			continue;
		}
		int k=z[i+1]/(i+1)+1;
		ans+=(k/2)*sum(tot);
		ans+=((k+1)/2)*sum(suf);
		++cnt[pre];
	}
	cout<<ans<<"\n";
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int T;
	cin>>T;
	while(T--) solve();
	return 0;
}

本质不同子串数

考虑增量算法，假设我们已经求出了某个后缀 \(S[i+1\cdots n]\) 的本质不同子串数，我们只需要求加入 \(S_i\) 后会产生多少新的本质不同字串，即多少前缀在之前没出现过，显然对 \(S[i\cdots n]\) 求 Z 函数，对于 \(S[i\cdots n]\) 的某个长度为 \(j\) 的前缀，如果某个 \(i<i\le n\) 满足 \(z_{i'}\ge j\) 则 \(j\) 是 \(S[i'\cdots n]\) 的一个前缀，因此所有新增子串长度 \(> z_{\max}\)，然后贡献就是 \(i-z_{max}\)

时间复杂度 \(\Theta(n^2)\)

[UVAoj11022] - String Factoring

Problem Link

考虑区间 dp，用 \(dp_{l,r}\) 表示压缩 \([l,r]\) 得到的最短长度

显然可以枚举中间断点或者枚举每个前缀的最小整周期进行压缩

时间复杂度 \(\Theta(n^3)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=81;
int dp[MAXN][MAXN];
inline vector<int> compress(string S) {
	int n=S.length(); S="$"+S;
	vector <int> kmp(n+1);
	for(int i=2,j=0;i<=n;++i) {
		while(j!=0&&S[j+1]!=S[i]) j=kmp[j];
		if(S[j+1]==S[i]) ++j;
		kmp[i]=j;
	}
	vector <int> root(n);
	for(int i=1;i<=n;++i) {
		if(i%(i-kmp[i])==0) root[i-1]=i-kmp[i];
		else root[i-1]=i;
	}
	return root;
}
inline int solve(string S) {
	int n=S.length(); S="$"+S;
	memset(dp,0x3f,sizeof(dp));
	for(int i=1;i<=n;++i) dp[i][i]=1;
	for(int len=2;len<=n;++len) {
		for(int l=1,r=len;r<=n;++l,++r) {
			for(int k=l;k<r;++k) dp[l][r]=min(dp[l][k]+dp[k+1][r],dp[l][r]);
			auto rt=compress(S.substr(l,len));
			for(int k=l;k<=r;++k) {
				dp[l][r]=min(dp[k-rt[k-l]+1][k]+((k==r)?0:dp[k+1][r]),dp[l][r]);
			}
		}
	}
	return dp[1][n];
}
signed main() {
	string S;
	while(true) {
		cin>>S;
		if(S=="*") break;
		printf("%d\n",solve(S));
	}
	return 0;
}

三、自动机初步

Basic Definition

I. kmp 自动机

定义

Definition Link

实际上是单模式串匹配自动机，状态集合 \(\mathbf Q=\{0,1,\cdots ,|T|\}\)，起始状态 \(start=0\)，接受状态集合 \(\mathbf F=\{|T|\}\)，每个状态 \(i\) 表示当前读入的文本串 \(S\) 中的后 \(i\) 个字符与 \(T\) 的前 \(i\) 个位置构成极大长度的匹配

转移函数 \(\delta\) 定义如下：

\[\delta(i,c)=
\begin{cases}
i+1&S_{i+1}=c\\
0&i=0\text{ and }S_{i+1}\ne c\\
\delta(\pi_i,c) &i>0\text{ and }S_{i+1}\ne c
\end{cases}
\]

对 \(S\) 进行匹配实际上等价于每次在自动机上从 \(q\) 状态上转移到 \(\delta(q,S_i)\) 状态上

非平凡边集

设字符集为 \(\Sigma\) 显然 kmp 自动机的转移函数大小为 \(\Theta(|T|\times |\Sigma|)\)，不过注意到很多的边事实上都是连回到 \(0\) 状态的，称这些边为平凡的

事实上，我们有如下的结论：非平凡的边集大小为 \(\Theta(|T|)\) 级别

首先一类边（后向边）一定是 \(\Theta(|T|)\) 级别的，二类边都是平凡边，所以我们只需要考虑三类边（前向边）的数量

实际上，有如下的断言：所有前向边 \(j\gets i\)，\(|i-j|\) 的值两两不同，证明如下

假设 \(\delta(i,c)=j>0\)，我们只证明不存在前向边 \(j+1\gets i+1\)，对于拓展到任意 \(j+k\gets i+k\) 的过程也是类似的

考虑 \(\delta(i,c)=j\) 的一组必要条件：\(S_{j+1}=c,S_{i+1}\ne c\)

再考虑 \(\delta(i+1,c')=j+1\) 的一组必要条件，\(S_{j+1}=S_{i+1}\)

此时立即导出矛盾，故所有前向边的 \(|i-j|\) 的值是不同的

根据上面的断言，证明了三类边的数量也是 \(\Theta(|T|)\) 级别的

综上，非平凡边的数量是 \(\Theta(|T|)\) 级别的

II. 子序列自动机

定义

子序列自动机解决的是判断 \(T\) 是否是 \(S\) 的子序列的问题，先考虑常规的算法：

对于每个 \(T_i\) 找尽可能靠左的 \(S_j=T_i\) 进行匹配

这个贪心算法的正确性是可以证明的，此处略去，我们考虑如何用自动机解决这个问题

状态集合 \(\mathbf Q=\{\text {null},0,1,2,\cdots ,|S|\}\)，起始状态 \(start=0\)，接受状态集合 \(\mathbf F=\{0,1,2,\cdots ,|S|\}\)，每个状态标识当前 \(S\) 串匹配到了 \(j\) 位置

转移函数 \(\delta\) 定义如下：

\[\delta(i,c)=
\begin{cases}
\text{null}&i=\text{null}\text{ or }i=|S|\\
i+1&i\ne\text{null}\text{ and }i<|S|\text{ and }S_{i+1}=c\\
\delta(i+1,c)&i\ne\text{null}\text{ and }i<|S|\text{ and }S_{i+1}\ne c\\
\end{cases}
\]

此时对于 \(T\) 在子序列自动机上如果最终没有到 \(\text{null}\) 状态说明 \(T\) 是一个 \(S\) 的子序列

本质不同子序列计数问题

考虑建立子序列自动机，注意到一条子序列自动机上每条合法的路径都对应一个不同的子序列，因此拓扑排序逆序转移方案总数即可

时间复杂度 \(\Theta(|S|\times|\Sigma|)\)

III. 习题演练

[CodeForces808G] - Anthem of Berland

Problem Link

首先对模式串建立 kmp 自动机，然后考虑 dp，用 \(dp_{i,j}\) 表示文本串已经输入 \(S[1\cdots i]\)，且当前在自动机的 \(j\) 状态上，对于 \(\texttt a\sim\texttt z\) 直接转移，对于 \(\texttt ?\) 枚举是哪一个字母再转移

由于我们要进行重复匹配，要对转移函数 \(\delta\) 稍作修改，每次匹配到 \(|T|\) 后当成失配继续跑才行：

\[\delta(i,c)=
\begin{cases}
\delta(\pi_i,c) &i=|T|\\
i+1&i<|T|\text{ and } T_{i+1}=c\\
0&i<|T|\text{ and }i=0\text{ and }T_{i+1}\ne c\\
\delta(\pi_i,c) &i<|T|\text{ and }i>0\text{ and }T_{i+1}\ne c
\end{cases}
\]

每次用自动机转移即可，时间复杂度 \(\Theta(|S|\times |T|\times|\Sigma|)\)

#include<bits/stdc++.h> 
using namespace std;
const int MAXN=1e5+1,INF=1e9;
char S[MAXN],T[MAXN];
int dfa[MAXN][26],kmp[MAXN];
signed main() {
	scanf("%s%s",S+1,T+1);
	int m=strlen(S+1),n=strlen(T+1);
	for(int i=2,j=0;i<=n;++i) {
		while(j!=0&&T[j+1]!=T[i]) j=kmp[j];
		if(T[j+1]==T[i]) ++j;
		kmp[i]=j;
	}
	for(int i=0;i<=n;++i) {
		for(char c='a';c<='z';++c) {
			if(i<n&&T[i+1]==c) dfa[i][c-'a']=i+1;
			else dfa[i][c-'a']=(i==0)?0:dfa[kmp[i]][c-'a'];
		}
	}
	vector <vector<int> > dp(m+1);
	for(int i=0;i<=m;++i) dp[i].resize(n+1,-INF);
	dp[0][0]=0;
	for(int i=0;i<m;++i) {
		for(int j=0;j<=n;++j) {
			if(j==n) ++dp[i][j];
			if(S[i+1]=='?') {
				for(int c='a';c<='z';++c) {
					dp[i+1][dfa[j][c-'a']]=max(dp[i][j],dp[i+1][dfa[j][c-'a']]);
				}
			} else {
				dp[i+1][dfa[j][S[i+1]-'a']]=max(dp[i][j],dp[i+1][dfa[j][S[i+1]-'a']]);
			}
		}
	}
	int ans=dp[m][n]+1;
	for(int i=0;i<n;++i) ans=max(ans,dp[m][i]);
	printf("%d\n",ans);
	return 0;
}

[CodeForces625B] - War of the Corporations

Problem Link

同上题，建立 kmp 自动机进行 dp，设 \(|T|\) 为不合法状态，如果这个位置被修改成了 \(\texttt #\)，那么直接从 kmp 自动机上返回 \(0\) 状态

时间复杂度 \(\Theta(|S|\times |T|\times|\Sigma|)\)

#include<bits/stdc++.h> 
using namespace std;
const int MAXN=1e5+1,MAXM=31,INF=1e9;
int dp[MAXN][MAXM],kmp[MAXM],dfa[MAXM][26];
char S[MAXN],T[MAXM];
signed main() {
	scanf("%s%s",S+1,T+1);
	int n=strlen(S+1),m=strlen(T+1);
	for(int i=2,j=0;i<=m;++i) {
		while(j!=0&&T[j+1]!=T[i]) j=kmp[j];
		if(T[j+1]==T[i]) ++j;
		kmp[i]=j;
	}
	for(int i=0;i<m;++i) {
		for(char c='a';c<='z';++c) {
			if(c==T[i+1]) dfa[i][c-'a']=i+1;
			else dfa[i][c-'a']=(i==0)?0:dfa[kmp[i]][c-'a'];
		}
	}
	memset(dp,0x3f,sizeof(dp));
	dp[0][0]=0;
	for(int i=0;i<n;++i) {
		for(int j=0;j<m;++j) {
			dp[i+1][dfa[j][S[i+1]-'a']]=min(dp[i+1][dfa[j][S[i+1]-'a']],dp[i][j]);
			dp[i+1][0]=min(dp[i+1][0],dp[i][j]+1);
		}
	}
	int ans=INF;
	for(int i=0;i<m;++i) ans=min(ans,dp[n][i]);
	printf("%d\n",ans);
	return 0;
}

[51nod1202] - 子序列个数

Problem Link

考虑建立子序列自动机，不过用拓扑排序统计路径复杂度是 \(\Theta(|S|\times |\Sigma|)\) 的显然会超时，考虑一个等价的 dp，用 \(dp_{i,j}\) 考虑 \(S[1\cdots i]\) 子序列以 \(j\) 结尾的数量，并且用如下方式转移

\[dp_{i,j}=
\begin{cases}
1+\sum_kdp_{i-1,k}&j=a_i\\
dp_{i-1,j}&j\ne a_i
\end{cases}
\]

可以证明这个 dp 过程实际上和在子序列自动机上统计路径数量是等价的

注意到假如我们忽略 \(i\) 一维，那么每次转移只修改一个数，因此动态维护 \(\sum_{k}dp_{i,k}\) 转移即可

时间复杂度 \(\Theta(n)\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+1,MOD=1e9+7;
int a[MAXN],dp[MAXN];
signed main() {
	int n,sum=0;
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) scanf("%lld",&a[i]);
	for(int i=1;i<=n;++i) {
		int k=dp[a[i]];
		dp[a[i]]=(sum+1)%MOD;
		sum=(sum+dp[a[i]]+MOD-k)%MOD;
	}
	printf("%lld\n",sum);
	return 0;
}