同余

同余

带余数除法

带余数除法的定义与基本性质

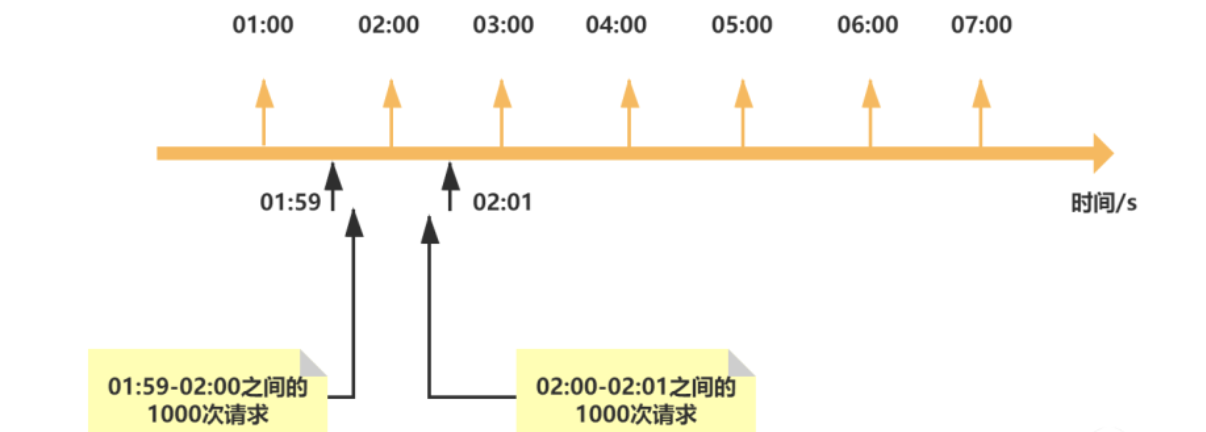
定义对于整数 \(a,b\) ，一定存在整数 \(q,r\) 满足 \(a = bq + r\) ，其中 \(r\) 与 \(a\) 同号且 \(|r| \in [0,b)\) ，称 \(q\) 为 \(a\) 除以 \(b\) 的商， \(r\) 为 \(a\) 除以 \(b\) 的余数。

通常我们定义 \(b\) 是正整数，但为了和c++语法统一，因此修改了定义。

模运算的定义 \(a \bmod b\) 表示 \(a\) 除以 \(b\) 的余数 \(r\) ，符号和 \(a\) 一致，运算优先级同乘除。

模 \(m\) 加法 \((a+b) \bmod m\) 。

模 \(m\) 减法 \((a-b) \bmod m\) 。

模 \(m\) 乘法 \(ab \bmod m\) 。

性质1 \(a \bmod b = a - b\times \lfloor \frac{a}{b}\rfloor\) 。

性质2

\[\begin{aligned}
a \bmod m \pm b \bmod m &= (a\pm b) \bmod m\\
(a \bmod m) \cdot (b \bmod m) &= ab \bmod m\\
(a \bmod m)^k &= a^k \bmod m
\end{aligned}
\]

性质3 \(a \bmod n = a\bmod m = x\) 且 \(\gcd(n,m) = 1\) ，则 \(a \bmod nm = x\)

模运算加速算法

龟速乘

用于可能爆 long long 数字的乘法取余。

不过一般可以用 __int128 替代了。

时间复杂度 \(O(\log b)\)

空间复杂度 \(O(1)\)

const int P = 1e9 + 7;
ll qmul(ll a, ll b) {
    ll ans = 0;
    while (b) {
        if (b & 1) ans = (ans + a) % P;
        b >>= 1;
        a = (a << 1) % P;
    }
    return ans;
}

快速幂

幂取余，\(a\) 越大速度越慢。

时间复杂度 \(O(\log k)\)

空间复杂度 \(O(1)\)

const int P = 1e9 + 7;
ll qpow(ll a, ll k) {
    ll ans = 1;
    while (k) {
        if (k & 1) ans = ans * a % P;
        k >>= 1;
        a = a * a % P;
    }
    return ans;
}

矩阵快速幂

矩阵幂取余。

时间复杂度 \(O(n^3 \log k)\)

空间复杂度 \(O(1)\)

const int P = 1e9 + 7;
struct Matrix {

    int n, m;//不能const，快速幂要复制
    vector<vector<ll>> mat;

    explicit Matrix(int _n):n(_n), m(_n), mat(_n + 1, vector<ll>(_n + 1)) {
        for (int i = 1;i <= n;i++)
            for (int j = 1;j <= m;j++)
                mat[i][j] = i == j;
    }//初始化n阶单位矩阵，explicit防止误用类型转换

    Matrix(int _n, int _m):n(_n), m(_m), mat(_n + 1, vector<ll>(_m + 1)) {}//初始化nxm零矩阵

    friend Matrix operator*(const Matrix &A, const Matrix &B) {
        Matrix ans(A.n, B.m);
        if (A.m != B.n) return ans;
        for (int i = 1;i <= A.n;i++)
            for (int j = 1;j <= B.m;j++)
                for (int k = 1;k <= A.m;k++) //a.m == b.n
                    ans.mat[i][j] = (ans.mat[i][j] + A.mat[i][k] * B.mat[k][j]) % P;
        return ans;
    }//矩阵乘法取余

    friend Matrix operator^(Matrix A, ll k) {
        Matrix ans(A.n);//A必须是方阵
        while (k) {
            if (k & 1) ans = ans * A;
            k >>= 1;
            A = A * A;
        }
        return ans;
    }//快速幂取余

    void output() const {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++)
                cout << mat[i][j] << ' ';
            cout << '\n';
        }
        cout << '\n';
    }//输出检测
};

同余的定义与基本性质

定义若整数 \(a,b\) 模 \(m\) 相等，则称 \(a,b\) 模 \(m\) 同余，记作 \(a \equiv b \pmod m\) 。

以下讨论均为整数。

性质1（自反性） \(a \equiv a \pmod m\) 。

性质2（对称性） \(a\equiv b \pmod m \iff b \equiv a \pmod m\) 。

性质3（传递性） \(a \equiv b \pmod m,b \equiv c \pmod m \Rightarrow a \equiv c \pmod m\) 。

性质4（同加性）

\[\begin{aligned}
a \equiv b \pmod m &\iff a \pm c \equiv b \pm c \pmod m\\
a \equiv b \pmod m,c \equiv d \pmod m &\iff a \pm c \equiv b \pm d \pmod m
\end{aligned}
\]

性质5（同乘性）

\[\begin{aligned}
a \equiv b \pmod m &\Rightarrow ac \equiv bc \pmod m\\
a \equiv b \pmod m,c \equiv d \pmod m &\Rightarrow ac \equiv bd \pmod m
\end{aligned}
\]

性质6（同幂性） \(a \equiv b \pmod m \Rightarrow a^k \equiv b^k \pmod m\) ，其中 \(k \geq 0\)。

性质7（特殊同除性） \(a \equiv b \pmod m \Rightarrow \dfrac{a}{d} \equiv \dfrac{b}{d} \pmod {\dfrac{m}{\gcd(m,d)}}\) ，其中 \(d\) 满足 \(d \mid a,d \mid b\) 。

性质8 \(a \equiv b \pmod m,m' \mid m \Rightarrow a \equiv b \pmod {m'}\) 。

性质9 \(a \equiv b \pmod {m_i}(i = 1,2,\cdots,n) \iff a \equiv b \pmod M ,M = \text{lcm}(m_1,m_2,\cdots,m_n)\) 。

性质10 \(a \equiv b \pmod m \Rightarrow \gcd(a,m) = \gcd(b,m)\) 。

同余类与剩余系的定义与基本性质

同余类的定义 对于 \(a \in [0,m-1]\) ，集合 \(\{a + km\},k \in \Z\) 的所有数模 \(m\) 同余 \(a\) ，称这个集合为模 \(m\) 的一个同余类 \(\overline a\) 。

完全剩余系的定义 模 \(m\) 的同余类有 \(m\) 个，分别为 \(\overline 0,\overline 1,\cdots ,\overline {m-1}\) ，它们构成了 \(m\) 的完全剩余系。

既约剩余系的定义 模 \(m\) 的同余类有 \(\varphi(m)\) 个的代表元与 \(m\) 互质，它们构成了 \(m\) 的既约剩余系（简化剩余系）。

\(\varphi(m)\) 为欧拉函数，下一节会讲到。

性质1 设 \(S\) 是模 \(m\) 的一个完全剩余系，若 \(\gcd(k,m) = 1\) ，则 \(S' = \{x' \mid x' = kx+b,x\in S \}\) 也是模 \(m\) 的一个完全剩余系。

性质2 设模 \(m_1\) 的完全剩余系为 \(S_1\) ，模 \(m_2\) 的完全剩余系为 \(S_2\) ，且 \(\gcd(m_1,m_2) = 1\) ，则模 \(m = m_1m_2\) 的完全剩余系为 \(S = \{x\mid x = m_2x_1 + m_1x_2,x_1 \in S_1,x_2 \in S_2\}\) 。

性质3 设 \(S\) 是模 \(m\) 的一个既约剩余系，若 \(\gcd(k,m) = 1\) ，则 \(S' = \{x' \mid x' = kx,x\in S \}\) 也是模 \(m\) 的一个既约剩余系。

性质4 设模 \(m_1\) 的既约剩余系为 \(S_1\) ，模 \(m_2\) 的既约剩余系为 \(S_2\) ，且 \(\gcd(m_1,m_2) = 1\) ，则模 \(m = m_1m_2\) 的既约剩余系为 \(S = \{x\mid x = m_2x_1 + m_1x_2,x_1 \in S_1,x_2 \in S_2\}\) 。

推论1（性质4的推论） \(\gcd(m_1,m_2) = 1 \Rightarrow \varphi(m_1m_2) = \varphi(m_1)\varphi(m_2)\) ，即欧拉函数是积性函数。

性质1的证明：

假设存在 \(kx_i + b \equiv kx_j + b \pmod m\) ，则 \(kx_i \equiv kx_j \pmod m\) 。因为 \(\gcd(k,m) = 1\) ，所以 \(x_i \equiv x_j \pmod m\) ，\(x_i,x_j\) 属于一个同余类，矛盾。综上，得证。

性质2的证明：

假设存在 \(m_2x_1 + m_1x_2 \equiv m_2x_1'+m_1x_2' \pmod m\) ，那么 \(m_2(x_1-x_1') \equiv m_1(x_2'-x_2) \pmod m\) 。因为 \(m_1 \mid m\) ，所以 \(m_2(x_1-x_1') \equiv m_1(x_2'-x_2) \equiv 0 \pmod {m_1}\) ，又 \(\gcd(m_1,m_2) = 1\) ，所以 \(x_1-x_1' \equiv 0 \pmod {m_1}\) ，矛盾。综上，得证。

性质3的证明：

根据性质1证明，类似可得 \(S'\) 一定是 \(m\) 的一个剩余系，且有 \(\varphi(m)\) 个元素，接下来只需证明任意元素都与 \(m\) 互质。

任意 \(x \in S\) ，有 \(\gcd(x,m) = 1\) ，又 \(\gcd(k,m) = 1\) ，所以 \(\gcd(kx,m) = 1\) ，所以 \(S'\) 是模 \(m\) 的既约剩余系。

性质4的证明：

根据性质2证明，类似可得 \(S\) 一定是模 \(m\) 的一个剩余系，且有 \(\varphi(m_1)\cdot\varphi(m_2)\) 个元素，但我们并不知道 \(\varphi(m_1)\cdot\varphi(m_2) = \varphi(m_1m_2)\) ，因此我们证明 \(S\) 的元素都与 \(m\) 互质只能说明 \(S\) 是模 \(m\) 的既约剩余系的一个子集，我们还需要证明模 \(m\) 的既约剩余系是 \(S\) 的一个子集。

若 \(\gcd(x_1,m_1) = \gcd(x_2,m_2) = 1\) ，又 \(\gcd(m_1,m_2) = 1\) ，因此 \(\gcd(m_2x_1,m_1) = \gcd(m_1x_2,m_2) = 1\) ，所以 \(\gcd(m_2x_1 + m_1x_2,m_1) = \gcd(m_1x_2+m_2x_1,m_2) = 1\) ，于是 \(\gcd(m_1x_2+m_2x_1,m_1m_2) = 1\) ，即 \(S\) 是模 \(m\) 的既约剩余系的子集。

因为 \(\gcd(m_1,m_2) = 1\) ，因此 \(m_2x_1+m_1x_2\) 可以表达所有整数。那么令模 \(m\) 的既约剩余系的元素为 \(m_2x_1+m_1x_2\) ，则 \(\gcd(m_2x_1+m_1x_2,m_1m_2) = 1\) ，因此 \(\gcd(m_2x_1+m_1x_2,m_1) = \gcd(m_2x_1+m_1x_2,m_2) = 1\) ，所以 \(\gcd(m_2x_1,m_1) = \gcd(m_1x_2,m_2) = 1\) ，又 \(\gcd(m_1,m_2) = 1\) ，于是 \(\gcd(x_1,m_1) = \gcd(x_2,m_2) = 1\) ，即模 \(m\) 的既约剩余系是 \(S\) 的子集。

综上 \(S\) 就是模 \(m\) 的既约剩余系。

推论1的证明：

由性质4，可得 \(S\) 的元素个数是 \(\varphi(m_1)\varphi(m_2)\) ，而模 \(m\) 的既约剩余系的元素个数是 \(\varphi(m_1m_2)\) 。因此，当 \(\gcd(m_1,m_2) = 1\) ， \(\varphi(m_1m_2) = \varphi(m_1)\varphi(m_2)\) ，即欧拉函数是积性函数。

欧拉函数

欧拉函数的定义与基本性质

定义 \([1,n]\) 中与 \(n\) 互质的个数记作 \(\varphi(n)\) 。

性质1 \(\varphi(p) = p-1\) ，其中 \(p\) 为素数。

性质2 \(\varphi(p^k) = p^k - p^{k-1}\) ，其中 \(k\in \Z^+\) ， \(p\) 为素数。

性质3 欧拉函数是积性函数，即 \(\gcd(a,b) = 1 \Rightarrow \varphi(ab) = \varphi(a)\cdot \varphi(b)\) 。

性质4 int 范围内欧拉函数的最大值为 \(1600\) 。

由性质1、2、3可以得到引理：

引理1（欧拉函数的展开式）

\[\begin{aligned}
\varphi(n) &= \varphi\bigg( \prod_{i = 1}^k p_i^{c_i} \bigg)\\
&= \prod_{i = 1}^k\varphi (p_i^{c_i}) \\
&= \prod_{i = 1}^k (p_i^{c_i}-p_i^{c_i-1})\\
&= n\prod_{p\mid n}\bigg(1-\frac{1}{p}\bigg)
\end{aligned}
\]