图神经网络 (GNN) 是一系列神经网络,可以自然地对图结构数据进行操作。与孤立地考虑单个实体的模型相比,通过从底层图中提取和利用特征,GNN 可以对这些交互中的实体做出更明智的预测。 GNN 并不是唯一可用于对图结构化数据进行建模的工具:图内核和随机游走方法层级是一些最流行的工具。然而,今天,GNN 在很大程度上取代了这些技术,因为GNN具有更好地对底层系统进行建模的固有灵活性。
图的计算挑战
缺乏一致的结构
节点个数,边的连接方法的多样性使得图成为一个灵活的但是难以计算的数学模型。
用可以计算的格式来表示图是非常重要的,最终选择的表示方法通常取决于实际问题。
节点顺序无关性
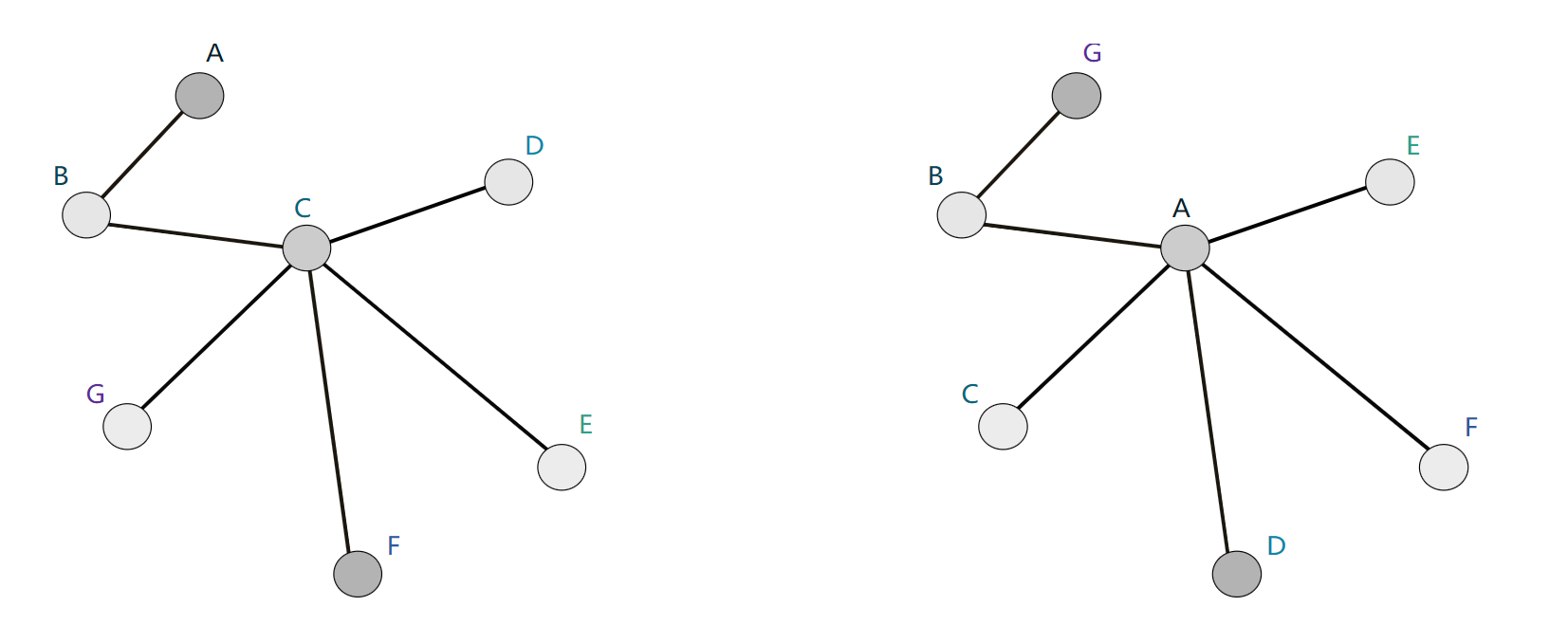
图的算法不应该依赖于节点的顺序。如果我们以某种方式置换节点,那么由我们的算法计算得到的节点表示也应该以相同的方式置换。
可扩展性
图表可以非常大!如Facebook 和 Twitter 等社交网络,它们拥有超过 10 亿用户。对这么大的数据进行操作并不容易。 幸运的是,大多数自然出现的图都是“稀疏的”:它们的边数往往与其顶点数成线性关系。另外的,通常如此庞大的网络会有少数节点拥有大量的边,如微博的大V,明星等。由于图的稀疏特性,这允许使用聪明的方法来有效地计算图中节点的表示。此外,与它们操作的图的大小相比,我们在GNN看到的方法将具有显着更少的参数。
图网络问题分类
1.节点分类
2.图分类
3.节点聚类
4.链路预测
5.影响力最大化
一些表示定义:
$ h_i^{(k)} $ :节点v在第k轮迭代(一次迭代可以看作是一个卷积层)时的表示,是一个向量;
G,V,E分别代表图,节点集合,边集合
卷积在图上的扩展
卷积神经网络在从图像中提取特征方面被认为非常强大。然而,图像本身可以被视为具有非常规则的网格状结构的图形,其中单个像素是节点,每个像素的 RGB 通道(3 chnnels)值作为节点特征。 因此,一个自然的想法是考虑将卷积推广到任意图。然而,回想一下上一节中列出的挑战:特别是,普通卷积不是节点顺序不变的,因为它们取决于像素的绝对位置。最初不清楚如何将网格上的卷积推广到一般图上的卷积,其中邻域结构因节点而异。好奇的读者可能想知道是否可以执行某种填充和排序来确保节点间邻域结构的一致性。这已经尝试并取得了一些成功,但我们将在这里看到的技术更加通用和强大。
我们首先介绍在节点邻域上构建多项式滤波器(其后的ChebyNet是在此基础上进行改进)的想法,就像 CNN 如何在相邻像素上计算局部滤波器一样。然后,我们将看到最近的方法如何通过更强大的机制扩展这个想法。最后,我们将讨论可以使用“全局”图级信息来计算节点表示的替代方法。
图上的多项式滤波器
图的拉普拉斯矩阵
$ L = D - A $ ,其中D是图的度矩阵,只有正对角线上有每个节点的度数,其余元素为0;A是邻接矩阵。
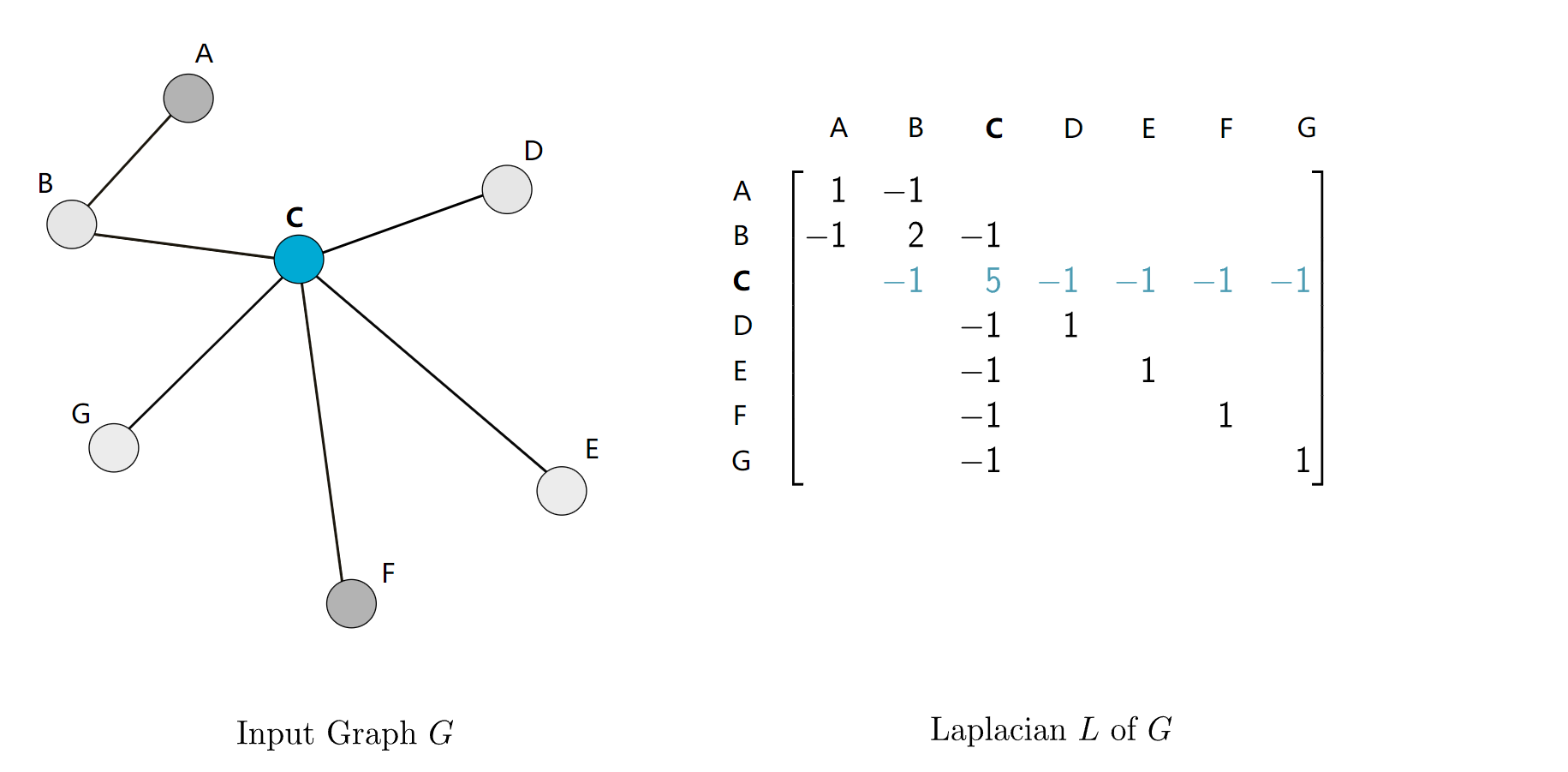
对于拉普拉斯矩阵,他所能编码的信息与邻接矩阵完全一样,因为知道了两个矩阵中的任意一个总能推出另外一个。但是拉普拉斯算子具有很多有用的性质,一些经典的算法都是在拉普拉斯矩阵实现的,如随机游走,谱聚类和扩散等。
拉普拉斯多项式
\]
我们首先考虑以以上的多项式作为图卷积核,即 $ x^{'} = p_w(L) x $ .我们可以将所有的系数总结为一个系数向量即$ w = [w_0, w_1, w_2, ... , w_d] $
接下来我们探讨为什么会想到使用这样的一个多项式来作为卷积核。
(1) 首先,当$ w_0 = 1 $,而其他的系数都是0时:
$$ x^{'} = p_w(L) x = I_nx = x $$,此时过滤后的结果就是原来的向量;
(2)接下来,考虑当$ w_1 = 1 ,而其他的系数都是0时:
x^{'} &= p_w(L) x\\
&= Lx \\
那么对于其中一个具体的节点v \hfill \\
x^{'}_v &= (Lx)_v \\ &= L_vx\\
&= \sum_{u\in G} L_{vu}x_u \\&= \sum_{u\in G} (D_{vu}-A_{vu})x_u \\&= \sum_{u\in G} D_{vu}x_u-\sum_{u\in G}A_{vu}x_u \\&=D_vx_v - \sum_{u\in \mathcal{N}(v)}x_u
\end{aligned}
\]
我们看到每个节点 $ v $ 的特征与其直接邻居包括自身的特征相结合。那么所选用的系数究竟与多项式的度\(d\) 有什么关系呢?我们可能会有一些合理的猜测,如果多项式k阶度作为核,那么过滤的结果的结果就只会与该节点的k阶邻居有关。事实上,这个猜测是正确的,我们通过选取多项式度可以控制节点特征的聚合范围,即能够实现局部性,这也是选用多项式核的一个重要因素,这大大减少了计算的复杂度,因为它避免了对拉普拉斯矩阵进行特征值分解(这将是\(O(n^3)\) 的复杂度)。
为了证明上面的假设,有一个拉普拉斯算子的性质很关键:
\]
自然语言解释为:在一个图中,若两节点的距离大于i,那么该图的拉普拉斯矩阵的i次幂该位置元素就是0.
当我们用多项式度d来进行卷积时:
x^{'}_v & = (p_w(L)x)_v \\&= (p_w(L))_vx \\&= \sum_{i=0}^d w_iL_v^ix \\&= \sum_{i=0}^d w_i \sum_{u \in G} L_{vu}^ix_u \\&= \sum_{i=0}^d w_i \sum_{u \in G \atop distG(v,u)\le i} L_{vu}^ix_u
\end{aligned}
\]
显然,以上的假设得以证明。
ChebNet
那么基于上一小节的拉普拉斯多项式卷积核,我们可以引申出ChebNet。
首先我们需要知道第一类切比雪夫多项式如下所示:
&T_0(x) = 1 \\
&T_1(x) = x \\
&T_{n+1}(x) = 2xT_n(x) - T{n-1}(x).
\end{aligned}
\]
通过切比雪夫多项式构造卷积核:
\]
那么为什么做出这样的选择:
(1)关于标准化拉普拉斯矩阵,即使用$ \tilde{L} $ 而不是$ L $:
L是一个半正定矩阵,这代表他的特征值$ \lambda \ge 0$ , 如果有大于1的特征值,那么在高阶的多项式的项中,值会急剧增大。进行标准化后,就将特征值的范围限定在$ [-1,1] $ 了,这样就解决了这个问题。
(2)关于使用切比雪夫多项式:
属于数学方面的问题,不多深究此处了。但是切比雪夫多项式有很多有趣的性质。
多项式滤波器实现了节点顺序无关性
题目所述的事实很容易在多项式的度为1时被证明。即当只使用一阶多项式时,过滤后的特征仅与邻居节点特征的和相关,显然sum操作与节点的顺序无关。更高次的多项式节点顺序无关性也可以类似的得到证明。
嵌入计算
我们现在来继续了解如何通过stack ChebNet层(或其他的多项式核)来构建一个图神经网络。

整合即为:
\]
每一层都有一个待学习的参数\(w^{(k)}\),它是该层的多项式卷积核的系数。过滤后再使用一个非线性的激活函数。
只需要叠加卷积层即可,但通常只需要2至3层即可达到最好的效果。
现代图神经网络
ChebNet 是在图上学习局部化过滤器的一个突破,它促使许多人从不同的角度思考图卷积。
我们可以把整个图卷积的过程分为两步:
(1)聚合节点周围的信息(k阶邻居,k由多项式的次数决定);
(2)将(1)中得到的信息与自身节点信息相结合并更新。
只要确保第一步聚合操作是节点顺序无关性的,那么整个卷积操作都是节点顺序无关性的。这些卷积操作可以看作是相邻节点的信息传递过程,在每一次迭代后,每一个节点都会从他的邻居节点接收到一些信息。在重复的迭代K次后,一个节点最终的感受域基本上能涵盖所有的节点即整个图。
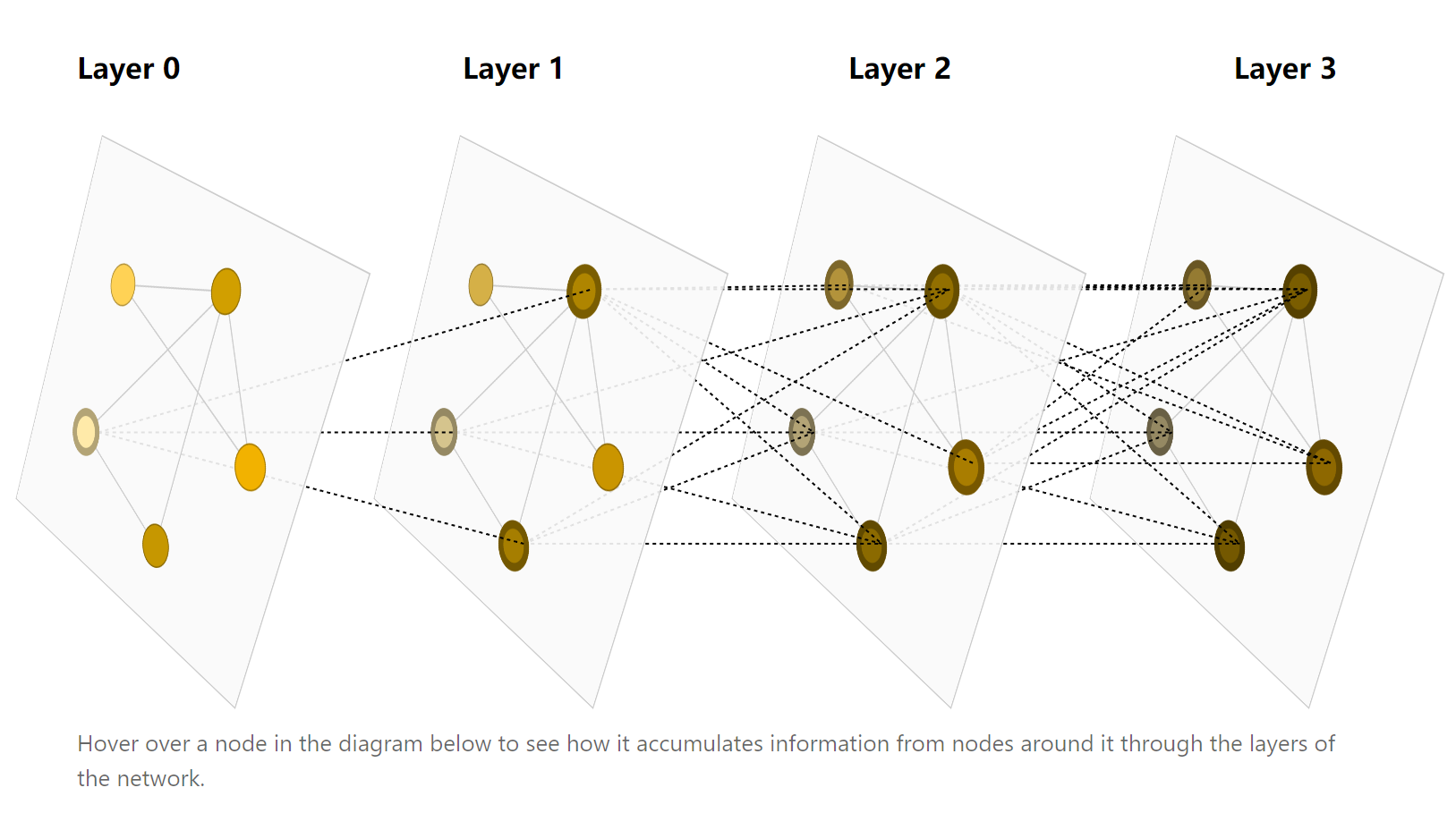
嵌入计算
消息传递机制构成了当今许多 GNN 架构的支柱。我们将在下面深入描述最受欢迎的几种神经网络:
Graph Convolutional Networks (GCN)
Graph Attention Networks (GAT)
Graph Sample and Aggregate (GraphSAGE)
Graph Isomorphism Network (GIN)
(未完待续)
声明:本文大部分译自Understanding Convolutions on Graphs,原文中有丰富的交互图帮助理解,推荐阅读。