引言

组合数学研究的主要问题：

存在性问题
计数和分类问题
构造性问题
优化问题

幻方问题

幻方的定义

幻方：一个 n 阶幻方是由整数 1，2，3…，n^2 按下述方式组成的 n×n 方阵：该方阵每行上的整数的和、每列上的整数的和以及两条对角线中每条对角线上的整数的和都等于同一个数

幻和 S：每一行（或列或对角线）数字的和

\[1+2+3+...+n^2=\frac{n^2\left( n^2+1 \right)}{2}
\\
n\cdot S=\frac{n^2\left( n^2+1 \right)}{2}
\\
S=\frac{n\left( n^2+1 \right)}{2}
\]

幻方的存在性问题

不存在二阶幻方（反证法）

幻方的构造性问题

奇数阶幻方的构造：连续摆放法：

将 1 放在 (n+1)/2 列第 1 行的方格中；
按照副对角线方向（即行号减1，列号加1）依次把从小到大的各个数字放入相应的方格中；
如果行号变成0（第 1 行上面一行），则改成第 n 行相应列对应的方格；
如果列号变成 n+1（第 n 列右面一列），则改成第 1 列相应行对应的方格；
如果轮到的方格已经填有数字或者到了第 0 行第 n+1 列对应的方格，则退到前一个方格正下方的方格.

????举例：构造五阶幻方

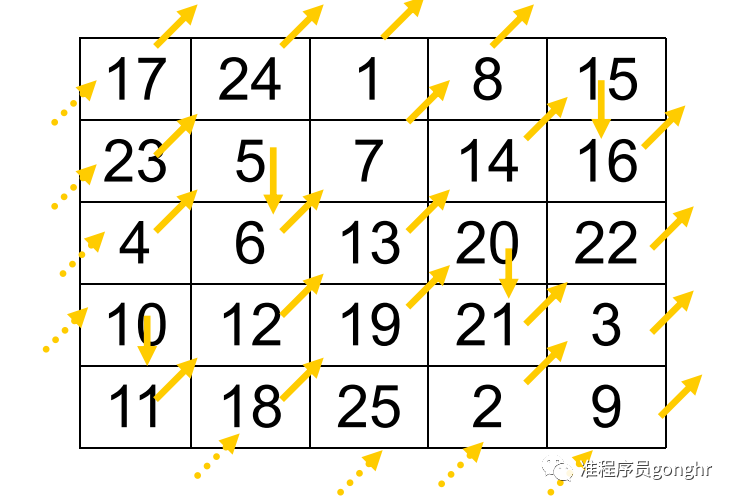
偶数阶幻方的构造：n=4k 对称法：

把 n×n 的方阵分成上、下、左、右四个 2k×2k 的方阵；
处理左上的 2k×2k 方阵，每行每列任意取一半(k个) 的方格做标记，涂成阴影；
按对称轴将阴影向下和向右作对称图形，使得 n×n 的方阵的每一行和每一列都有一半(n/2)的方格被涂成阴影；
从 1 开始依次填入方格中，第一遍：从第 1 行第 1 列的方格开始往右，不是阴影则填数字，是阴影的方格不填数字，但相应的数字加 1. 第 1 行填完后填第 2 行依次到第 n 行第 n 列的方格；
第二遍：从第 n 行第 n 列的方格开始依次往左，规则同前，从 1 开始的数字依次填入，第 n 行结束之后是第 n-1 行第 n 列的方格，直到第 1 行第 1 列的方格

????举例：构造四阶幻方

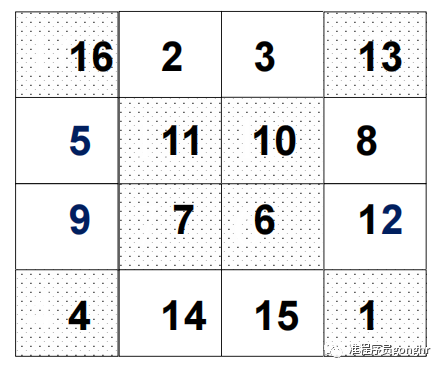
单偶数阶幻方 n=4k+2：

把 n×n 的方阵分成上、下、左、右四个 (2k+1)×(2k+1) 的方阵，编为左上A、右下B、右上C、左下D；
把1～(2k+1)^2放在 A 中做成第一个幻方；
把 (2k+1)^2＋1～2(2k+1)^2 放在 B 中成第二个幻方；
把 2(2k+1)^2＋1～3(2k+1)^2 放在 C 中成第三个幻方；
把 3(2k+1)^2＋1～4(2k+1)^2 放在 D 中成第四个幻方；
在 A 的各行从第 1 列开始向右取 m 个(m=(n-2)/4)方格，但中间一行（k+1行）从第 2 列开始；把这些方格中的数字与 D 中相应位置的数字对换；
在 C 中各行最后一列右起向左各取 m-1 个方格，把这些方格中的数字与 B 中相应位置的数字对换

????举例：构造六阶幻方

填充

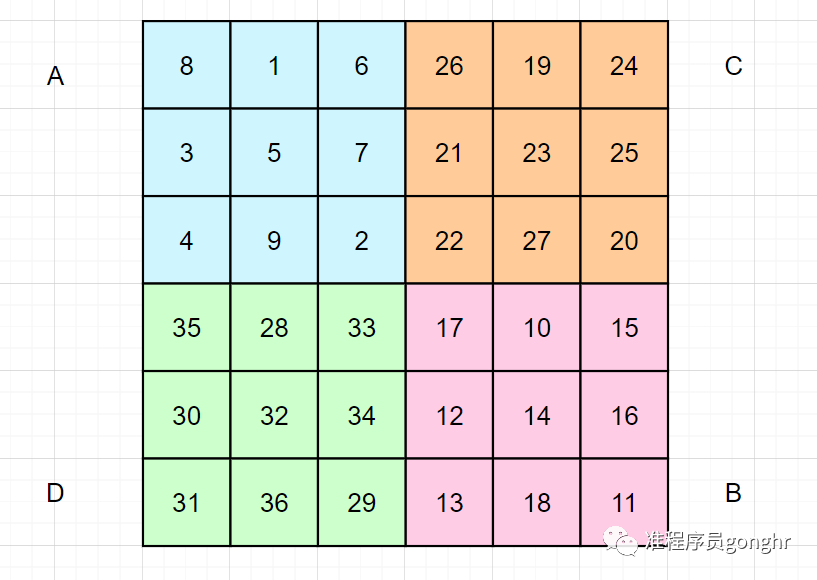
对换
m = (n-2)/4 = (6-2)/4 = 1

拉丁方问题

拉丁方的定义

n 阶拉丁方：由数字 1,2,…,n 构成的 n×n 的方阵,使得在每 1 行、每 1 列中每个数字都恰好出现一次.

拉丁方的存在性问题

2 阶拉丁方存在

拉丁方的构造性问题

n阶拉丁方的构造方法：

正交拉丁方

三十六军官问题：有 36 名军官来自 6 个不同的军团，共有 6 种不同的军衔，他们能否排成一个 6*6 的方阵，使得每行每列恰有各种军衔，并且每行和每列上的不同军衔的 6 名军官还分别来自不同的军团？

解：从 n 个军团里选 n 个不同的军衔，能否排成一个 n*n 的方阵，使得每行每列恰有各种军衔，并且每行和每列上的不同军衔的 n 名军官还分别来自不同的军团？
把问题规模缩小到三阶可以得到：

正交拉丁方的定义：

\[\text{设}A=\left( a_{ij} \right) _{n\times n}\text{，}B=\left( b_{ij} \right) _{n\times n}\text{是两个}n\times n\text{拉丁方，令}C=\left[ \left( a_{ij},b_{ij} \right) \right] _{n\times n}\text{，若}C\text{的}n^2\text{对数组互不相同，则称}A\text{与}B\text{正交}
\\