马尔可夫过程(Markov process)是一类随机过程。由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性:在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变 (过去 )。例如森林中动物头数的变化构成——马尔可夫过程。在现实世界中,有很多过程都是马尔可夫过程,如液体中微粒所作的布朗运动、传染病受感染的人数、车站的候车人数等,都可视为马尔可夫过程。

一、马尔科夫决策理论
马尔科夫过程中最核心的几个概念:过去,现在,将来。马尔可夫模型(Markov Model)是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法、序列分类等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法之一。
1.1马尔科夫链
状态空间:马尔可夫链是随机变量\(X_1,X_2,X_3,…,X_n\)所组成的一个数列,每一个变量\(X_i\)都有几种不同的可能取值,他们所有可能取值的集合,被称为“状态空间”,而\(X_n\)的值则是在时间\(n\)的状态,状态空间记为\(S\)。
转移概率(Transition Probability):\(P_{ij}=P(x_{t+1}=j|x_t=i)\)表示在时刻\(t\)处于状态\(i\),在下一时刻\(t+1\)处于状态\(j\)概率,\(n\)是系统所有可能的状态个数。
\(P=[P_{ij}]_{n∗n}\),对于任意\(i \in S\),都有 \(\sum_{j=1}^{n}{[P_{ij}]} = 1\)
马尔可夫链可以用条件概率模型来描述。我们把在前一时刻某取值下当前时刻取值的条件概率称作转移概率。
设随机过程\(X_n(n\in T)\)的时间集合\(T = \{1,2,3,…\}\),状态空间\(E = \{1,2,3…N\}\),即\(X_n (n\in T)\)是时间离散、状态离散的随机过程。若对任意的整数\(n\in T\),满足
\]
则称\(X_n(n\in T)\)为马尔可夫链,简称马氏链。上式称为过程的马尔可夫性或无后效性。
\(P_{ij}(n_m,n_{m+k})\)与\(n_m\)无关,即转移概率只与出发状态、转移步数、到达状态相关
\]
**设一步转移概率:\(P_{ij}(1) \leftrightarrow p_{ij}\),可证明:\(k\)步转移概率矩阵为一步转移概率矩阵的\(k\)次幂。
\]
转移概率矩阵:矩阵各元素都是非负的,并且各行元素之和等于1,各元素用概率表示,在一定条件下是互相转移的,故称为转移概率矩阵。如用于市场决策时,矩阵中的元素是市场或顾客的保留、获得或失去的概率。P(k)表示k步转移概率矩阵。
1.2 概率矩阵
由转移概率组成的矩阵就是转移概率矩阵,也就是说构成转移概率矩阵的元素是一个个的转移概率。
假定某大学有1万学生,每人每月用1支牙膏,并且只使用“中华”牙膏与“黑妹”牙膏两者之一。根据本月(12月)调查,有3000人使用黑妹牙膏,7000人使用中华牙膏。又据调查,使用黑妹牙膏的3000人中,有60%的人下月将继续使用黑妹牙膏,40%的人将改用中华牙膏; 使用中华牙膏的7000人中, 有70%的人下月将继续使用中华牙膏,30%的人将改用黑妹牙膏。据此,可以得到如表-1所示的统计表。
表-1 两种牙膏之间的转移概率
拟用 黑妹牙膏 中华牙膏
现用
黑妹牙膏 60% 40%
中华牙膏 30% 70%
上表中的4个概率就称为状态的转移概率,而这四个转移概率组成的矩阵
B=\begin{bmatrix}60% & 40%\30% & 70%\end{bmatrix}
称为转移概率矩阵。可以看出, 转移概率矩阵的一个特点是其各行元素之和为1。 在本例中,其经济意义是:现在使用某种牙膏的人中,将来使用各种品牌牙膏的人数百分比之和为1。
若存在\(m\)为正整数,概率矩阵\(P\)的\(m\)次幂\(P^m\) 的所有元素皆为正,则P称为正规概率矩阵。
*正则概率矩阵的这一性质很有实用价值。因为在市场占有率是达到平稳分布时,顾客(或用户)的流动将对市场占有率不起影响。即各市场主体丧失的顾客(或用户)与争取到的顾客相抵消。
*若马尔科夫链的一步转移概率矩阵P为正规概率矩阵,则马尔可夫链是遍历的。
*如存在概率向量\(x = (x_1,x_2,…,x_n)\),使得概率矩阵\(P\)满足:\(xP = x\),则称\(x\)为\(P\)的固定概率向量(特征向量)。特别地,若\(x\)为一状态概率向量,\(P\)为状态转移概率矩阵,则称\(x\)为对应马尔可夫链的一个平稳分布。
若任意的\(i,j\in S:\lim_{m\rightarrow +\infty}p_{ij}^{(m)} = \pi_j\),则称\(\pi = (\pi_1,\pi_2,…,\pi_N)\)为稳态分布。
设存在\(\pi = (\pi_1,\pi_2,…,\pi_N)\)稳态分布,则由于下式恒成立:\(P(k) = P(k-1)P\),令\(k\rightarrow \infty\)就得就得\(\pi = \pi P\)
- 若随机过程某时刻的状态概率向量为平稳分布,则称过程处于平衡状态。 一旦过程处于平衡状态,将永远处于平衡状态。
- 对于有限状态的马尔可夫链,平稳分布必定存在。特别地,当状态转移矩阵为正规概率矩阵时,平稳分布唯一。
- 状态
指某一件事在某个时刻(或时期)出现的某种结果。
2.状态转移过程
事件的发展,从一种状态转变为另一种状态,称为状态转移。
3.马尔可夫过程
在事件的发展过程中,若每次状态的转移都仅与前一时刻的状态有关,而与过去的状态无关,或者说状态转移过程是无后效性的,则这样的状态转移过程就称为马尔可夫过程。
4.状态转移概率
用于描述,在事件的发展变化过程中,从某一种状态出发,在下一时刻转移到其它状态的可能性大小。
转移概率矩阵
关于n阶转移矩阵我想在开例子后再介绍
为了求出每一个,一般采用频率近似概率的思想进行计算。
5.状态转移概率矩阵
例1:社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别,那么他的孩子属于下层收入的概率是0.65,属于中层收入的概率是0.28,属于上层收入的概率 是 0.07。事实上,从父代到子代,收入阶层的变化的转移概率如下:

使用矩阵的表示方式,转移概率矩阵记为
0.65 & 0.28 & 0.07\\
0.15 & 0.67 & 0.18\\
0.12 & 0.36 & 0.52
\end{matrix}\right]\]
假设当前这一代人处在下层、中层、上层的人的比例是概率分布向量\(π0= [ π0(1),π0(2),π0(3)]\),那么他们的子女的分布比例将是\(π1=π0P\),他们的孙子代的分布比例将是\(π2= π1P=π0P2, ….\),第\(n\)代子孙的收入分布比例将是\(πn= πn-1P=π0Pn, ….\)。假设初始概率分布为\(π0 =[0.21,0.68, 0.11]\),则我们可以计算前 \(n\) 代人的分布状况如下
例2: 假设在一个区域内,人们要么是住在城市,要么是住在乡村。下面的矩阵告诉我们人口迁移的一些规律(或倾向)。例如,第1行第一列就表示,当前住在城市的人口,明年将会有90%的人选择继续住在城市。

作为一个简单的开始,试着来计算一下现今住在城市的人中2年后会住在乡村的几率有多大。分析可知,当前住在城市的人,1年后,会有90%继续选择住在城市,另外10%的人则会搬去乡村居住。然后又过了1年,上一年中选择留在城市的人中又会有10%的人搬去乡村。而上一年中搬到乡村的人中将会有98%的选择留在乡村。这个分析过程如下图所示,最终可以算出现今住在城市的人中2年后会住在乡村的几率=0.90×0.10+0.10×0.98。
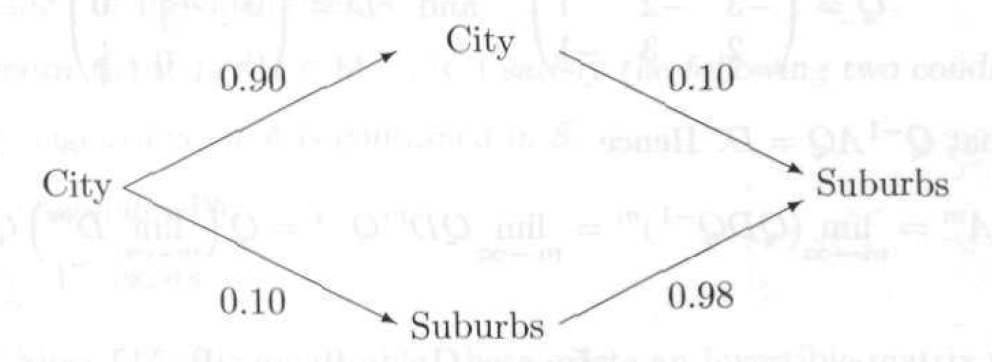
实你会发现我们的计算过程就是在做矩阵的平方。如下图所示,你会发现结果矩阵中第2行第1列的计算就是在执行上面在处理的操作。在此基础,我们还可以继续计算n年后的情况,也就是计算矩阵A自乘n次后的结果。
如果我们假设最开始的时候,城乡人口的比例为7:3,那么我们可以用一个列向量来表示它 P=[0.7, 0.3]T,我们想知道最终城乡人口的比例为何,则就是要计算。如果最初城乡人口的比例为9:1,结果又如何呢?这些都要借助矩阵的极限,对角化操作以及马尔科夫链等概念来辅助我们的计算。
例3:玩家和庄家对赌硬币,如果正面朝上,本轮玩家赢,庄家付给玩家 ⼀元;如果反面朝上,本轮玩家输,玩家付给庄家⼀元。假设玩家 ⼿上有10元硬币,⼿上钱⼀旦输光则退出游戏。(注:不考虑庄家输赢,只考虑玩家输赢;赌完一定局数后,仍然有10元硬币属于“Win”。)
例4:假设在某一固定选区美国国会选举的投票结果用 中的向量 表示为
假设我们用这种类型的向量每两年记录一次美国国会选举的结果,同时每次选举的结果仅依赖于前一次选举的结果,则刻画每两年选举的向量构成的序列是一个马尔可夫链。对此链,作为
个随机矩阵的例子,取

二、案例呈现
例:某地区有甲、乙、丙三家药厂生产板蓝根,有1600个用户,假定在研究期间无新用户加入也无老用户退出,只有用户的转移。已知 8月份有480 户是甲厂的顾客;320 户是乙厂的顾客;800户是丙厂的顾客。9 月份,甲厂的顾客有 48 户转乙厂,96户转丙厂;乙厂的顾客有32户转甲厂,64户转丙厂;丙厂有的顾客有 64户转甲厂,32户转乙厂。假设顾客保持相同的流转,请预测
(1)这三家药厂在10月和11月的顾客人数,
(2)稳态时市场的占有率。
| 从-到 | 甲 | 乙 | 丙 | 合计 |
|---|---|---|---|---|
| 甲 | 336 | 48 | 96 | 480 |
| 乙 | 32 | 224 | 64 | 320 |
| 并丙 | 224 | 32 | 704 | 800 |
| 合计 | 432 | 304 | 864 | 1600 |
状态转移概率矩阵:
\]
9月份的状态向量为(432,304,864),由
\]
可预测,10月份,甲、乙、丙三家的顾客数分别为(402,291,908)。
同理,
\]
可预测,11月份,甲、乙、丙三厂的顾客数分别为383、280、937。
\]
求得稳态分布:\(x^*= (0.2187,0.1563,0.6250)\)
所以三家药厂在均衡时的市场占有率分别是:甲22%,乙16%,丙62%。
二、案例呈现
在外地旅游时,为了出行方便,许多游客会选择租车出行。某公司在北京和天津两地开展汽车租赁业务,共投入7000辆车。消费者可以从任意一个城市租车,也可以任意还车到各个城市。需要解决的问题是如何分配最初的车辆布局可以让车辆利用率达到最大化。例如:从天津借出的车辆0.7还车在天津,0.3还车在北京。从北京借出的车辆0.6还车在北京,0.4还车在天津。故有简单数学式表示下一天车辆和当天车辆的表达式(假设每辆车都被借出去了):
& \begin{array}{llll}
&& a && b &&c &&d
\end{array} \\
& \begin{array}{l}
a \\
b \\
c\\
d
\end{array}\left[\begin{array}{llll}
0.7 & 0.2 & 0.0 & 0.1\\0.2 & 0.5 &0.2 &0.1 \\0.1& 0.1 &0.5 & 0.3 \\ 0.5 & 0.2 & 0.2 & 0.1
\end{array}\right] \\
&
\end{aligned}
\]
矩阵中的各个量表示从某地借车还车到某地的意愿。矩阵表示从某地借车还到某地情况下第一天还车和第二天还车的意愿,可以综合考虑两地之间的距离,出行目的等因素或直接进行调查分析。具体地:a,b,c,d为四个城市,其中从a城市租借的车辆在a城市规划的比例为p[0][0],b城市为a[0][1],c城市为p[0][2],d城市为p[0][3]。同理在b和c城租借的车辆在各个城市归还的比例分别表示为p[1][0]、p[1][1]、p[1][2]、p[1][3]和p[2][0]、p[2][1]、p[2][2]、p[2][3]。设定一个新的限制:租借的车辆并不需要及时归还。租借的车辆可以在租车起未来三天内自由归还。根据租客还车的喜好,可以设定每个租车人在两内的每天的换车比例。例如第一天归还的比例占0.7,第二天归还比例占0.3。为了和实际情况靠近,考虑各城市之间的距离,设定模拟超参数,判断用户需要将车从某城还往某城时,选择第一天第二天还车的意愿。利用矩阵运算可以很好处理这样的问题。
三、Python处理
从问题出发,显然利用numpy模块进行矩阵运算非常方便。需要特别注意的是第一天借出的车辆由于一部分用户决定隔一天还,故第一天的情况需要单独处理。之后利用循环迭代便可得到结果。显然可知,车辆数量一定的情况下,车辆在各个城市的分布最终会达到平衡。可以以此为基础分配最初的车辆分布情况,提高汽车的利用率。
import matplotlib.pyplot as plt
import numpy as np
#计算稳态概率
p = np.array([[0.7,0.2,0.0,0.1],[0.2,0.5,0.2,0.1],[0.1,0.1,0.5,0.3],[0.5,0.2,0.2,0.1]])
r_1 = np.array([[0.8,0.6,0.4,0.2],[0.3,0.7,0.1,0.4],[0.4,0.3,0.8,0.2],[0.2,0.5,0.4,0.8]])
r_2 = np.array([[0.2,0.4,0.6,0.8],[0.7,0.3,0.9,0.6],[0.6,0.7,0.2,0.8],[0.8,0.5,0.6,0.2]])
amount_per_day = {}
amount = np.array([1000,300,600,800])
amount_per_day[0] = amount
amount_per_day[1] = np.dot(np.multiply(p,r_1).transpose(),amount.transpose())#第一天单独处理
for i in range(2,21):
amount_per_day[i] = np.dot(np.multiply(p,r_1).transpose(),amount_per_day[i - 1].transpose())+\
np.dot(np.multiply(p,r_2).transpose(),amount_per_day[i - 2].transpose())
amount_per_day[i] = np.array(list(map(int, amount_per_day[i][:])) ) #每次循环都取整
print(amount_per_day[20])
#结果可视化
a = []
b = []
c = []
d = []
for j in range(21):
a.append(amount_per_day[j][0])
b.append(amount_per_day[j][1])
c.append(amount_per_day[j][2])
d.append(amount_per_day[j][3])
wang_numpy = np.arange(0,21,1)
plt.plot(wang_numpy,a,'r--')
plt.plot(wang_numpy,b,'b--')
plt.plot(wang_numpy,c,'g--')
plt.plot(wang_numpy,d,'m--')
plt.xlabel('iteraitons or days')
plt.ylabel('number of cars')
plt.xticks(np.arange(0, 21, 1))
plt.grid(True)
plt.show()

总结
马尔可夫模型(Markov Model)是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。马尔科夫过程具有在给定当前知识或信息的情况下,过去(即当期以前的历史状态)对于将来(即当期以后的未来状态)是无关的。
参考文献
4.6 杰克租车问题
杰克管理一个全国性汽车出租公司的两个地点。每天一些顾客到这两个地点租车。如果有车可租,杰克就将车租出并从公司得到10美元的回扣。如果这个地点没车,杰克就失去了这笔生意。还回的车第二天就可以出租。为了使需要车的地点有车可租,每天晚上,杰克可以在两个地点间移动车辆,移动每辆车的费用是2美元。我们假设每个地点的车的需求量和归还量都是泊松分布变量。假设租车的期望值是3和4,还车的期望值是3和2。为了简化问题,我们假设每个地点的车不多于20辆(多于的车被还回公司,在此问题中消失了)并且一晚上最多移动5辆车。折扣率为0.9,并描述为一个有限MDP问题,时刻按天计算,状态是每天结束时两个地点的车辆数,动作是晚上在两个地点间移动的车辆数。
重心问题
重心问题指有些公共服务设施 (例如邮局, 学校等) 的选址, 要求设施到所有服务对象点的距离总和最小. 一般要考虑人口密度问题, 或者全体被服务对象来往的总路程最短. 例如下面的问题:
某矿区有六个产矿点, 如图所示, 已知各产矿点每天的产矿量 (标在图中的各顶点旁) 为 q i ( i = 1 , 2 , ⋯ , 6 ) q_{i}(i=1,2, \cdots, 6) qi(i=1,2,⋯,6) 吨, 现要从这六个产矿点选一个来建造选矿厂, 问应选在哪个产矿点, 才能使各产矿点所产的矿石运到选矿厂所在地的总运力 (吨·公里) 最小.

令 d i j ( i , j = 1 , 2 , ⋯ , 6 ) d_{i j}(i, j=1,2, \cdots, 6) dij(i,j=1,2,⋯,6) 表示顶点 v i v_{i} vi 与 v j v_{j} vj 之间的距离. 若选矿厂设在 v i v_{i} vi 并且各产矿点到选矿厂的总运力为 m i m_{i} mi, 则确定选矿厂的位置就转化为求 m k m_{k} mk, 使得 m k = min 1 ≤ i ≤ 6 m i m_{k}=\min _{1 \leq i \leq 6} m_{i} mk=min1≤i≤6mi.
由于各产矿点到选矿厂的总运力依赖于任意两顶点之间的距离, 即任意两顶点之间最短路的长度, 因此可首先利用 Dijkstra (或 Floyd) 算法求出所有顶点对之间的最短距离, 然后计算出顶点 v i v_{i} vi 设立选矿厂时各产矿点到 v i v_{i} vi 的总运力
m i = ∑ j = 1 6 q j d i j , i = 1 , 2 , ⋯ , 6. m_{i}=\sum_{j=1}^{6} q_{j} d_{i j}, \quad i=1,2, \cdots, 6. mi=j=1∑6qjdij,i=1,2,⋯,6.
最后利用 min 1 ≤ i ≤ 6 m i \min _{1 \leq i \leq 6} m_{i} min1≤i≤6mi 选择设置选矿厂的位置.
计算的 Python 程序如下:
import numpy as np
import networkx as nx
List=[(1,2,20),(1,5,15),(2,3,20),(2,4,40),
(2,5,25),(3,4,30),(3,5,10),(5,6,15)]
G=nx.Graph()
G.add_nodes_from(range(1,7))
G.add_weighted_edges_from(List)
c=dict(nx.shortest_path_length(G,weight='weight'))
d=np.zeros((6,6))
for i in range(1,7):
for j in range(1,7): d[i-1,j-1]=c[i][j]
print(d)
q=np.array([80,90,30,20,60,10])
m=d@q #计算运力,这里使用矩阵乘法
mm=m.min() #求运力的最小值
ind=np.where(m==mm)[0]+1 #python下标从0开始,np.where返回值为元组
print("运力m=",m,'\n最小运力mm=',mm,"\n选矿厂的设置位置为:",ind)
[[ 0. 20. 25. 55. 15. 30.]
[20. 0. 20. 40. 25. 40.]
[25. 20. 0. 30. 10. 25.]
[55. 40. 30. 0. 40. 55.]
[15. 25. 10. 40. 0. 15.]
[30. 40. 25. 55. 15. 0.]]
运力m= [ 4850. 4900. 5250. 11850. 4700. 8750.]
最小运力mm= 4700.0
选矿厂的设置位置为: [5]
min 1 ≤ i ≤ 6 m i = m 5 \min _{1 \leq i \leq 6} m_{i}=m_{5} min1≤i≤6mi=m5, 所以 v 5 v_{5} v5 为设置选矿厂的位置