马尔科夫不等式（Markov inequality）

任取非负随机变量$ X $，则 $ \forall a>0$ 有 $ P(X\ge a)\le \frac{E(X)}a$

证明：任取 \(a>0\) ，设 \(Y_a=\begin{cases} 0 & (X<a)\\ a & (X\ge a)\end{cases}\)，有\(E(Y_a)=aP(X\ge a)\)。

而$(Y_a\le X) \to (E(Y_a)\le E(X))\to $

\((aP(X\ge a)\le E(x))\to (P(X\ge a)\le \frac{E(x)}a)\)

这个定理的意义是，对于一个正的随机变量，他取到一个远大于期望值的概率是非常小的。

知乎上有一个有意思的图片证明：令\(y(x)=\begin{cases} 0 & (x<b)\\ 1 & (x\ge b)\end{cases}\)，那么\((\forall x)y(x)\le \frac xb\)，那么带入大\(X\)也成立。

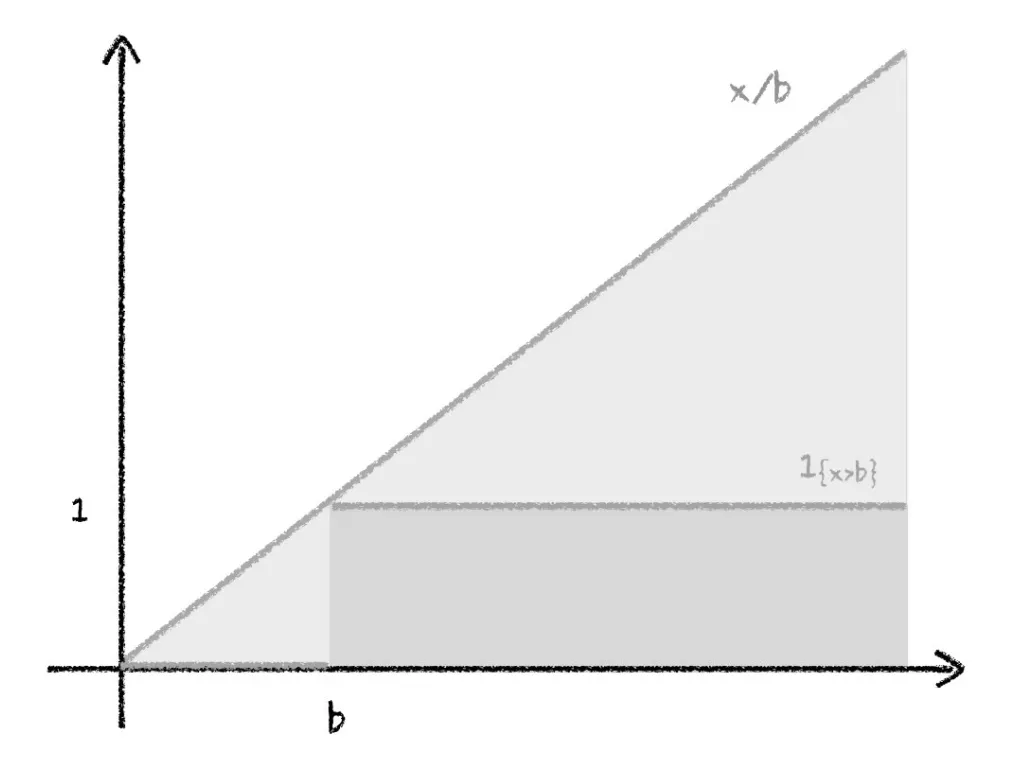
同时取期望，显然 \(E(y(x))=\int_b^{\infty}f(x)dx= P(X\ge b)\le \frac {E(x)}b\)

知乎回答：https://www.zhihu.com/question/27821324/answer/80814695

切比雪夫不等式（Chebyshev Inequality）

任取随机变量$ X $， \(E(X)= \mu , D(x)=\sigma^2\)，则$ \forall \varepsilon>0 $ 有 $ P( |X-\mu | \ge \varepsilon)\le \frac {\sigma^2} {\varepsilon^2} $

（或者是取\(k\)倍标准差的版本，即$ P( |X-\mu | \ge k\sigma)\le \frac 1k $）

证明：\(P( |X-\mu | \ge \varepsilon)=\int_{|X-\mu|\ge\varepsilon}f(x)d x\)

而 \((\frac{x-\mu}\varepsilon)^2\ge 1\)，所以 上式

\(\le\int_{|X-\mu|\ge\varepsilon}(\frac{x-\mu}\varepsilon)^2f(x)d x\le \int_{-\infty}^{\infty}(\frac{x-\mu}\varepsilon)^2f(x)d x\)

\(=\frac 1{\varepsilon^2} \int_{-\infty}^{\infty}({x-\mu})^2f(x)d x=\frac {\sigma^2} {\varepsilon^2}
\)

也可以从马尔科夫不等式的角度看。$ P( (X-\mu )^2 \ge \varepsilon^2)\le \frac {(X-\mu)^2} {\varepsilon^2}=\frac {\sigma^2} {\varepsilon^2} $，而 $ P( (X-\mu )^2 \ge \varepsilon^2) $和 $ P( |X-\mu | \ge \varepsilon) $ 是一样的，所以就成立了。

切比雪夫不等式除了期望，还引入了方差来估计概率，因此更加准确（当然两个不等式的界其实都是非常松散的）

这个定理的意义是，一个随机变量，他取到一个离期望很远的值的概率是很小的，方差越大，概率减少的越快。

知乎那个回答也贴出了这个定理的图示：

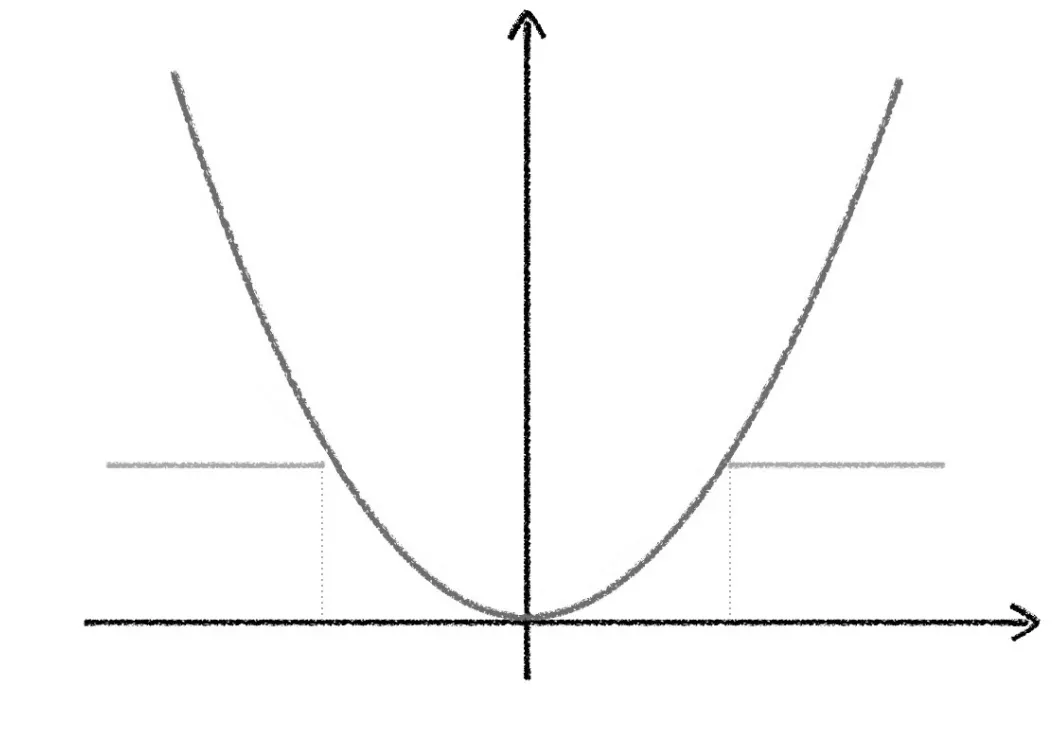
令\(y(x)=\begin{cases} 0 & (|x-a|>b)\\ 1 & else\end{cases}\)，那么\((\forall x)y(x)\le \frac {(x-a)^2}{b^2}\)，同时取期望有\(P(|x-a|>b)\le \frac {E((x-a)^2)}{b^2}\le \frac{D(x)}{b^2}\)。

推荐阅读：大数定律和中心极限定理