旅行商问题（TSP）作为世界上著名的NP难题之一，仍然吸引着大批学者的研究。解决该问题的算法也种类繁多，一些启发式、半启发式算法在该问题上广为应用，包括像遗传算法、模拟退火、蚁群算法、粒子群优化算法等解法也颇为常见。

一、旅行商问题的数学模型

旅行商问题 (简称TSP)是运筹学中一个著名的问题, 其一般提法为:

有一个旅行商从城市 1 出发, 需要到 城市2、3、...、n去推销货物, 最后返回城市 1 , 若任意两个城市间的距离已知, 则该旅行商应如何选 择其最佳行走路线?
TSP在图论意义下又常常被称为最小Hamilton圈问题, Euler等人最早研究了该问题的雏形, 后来由英国的 Hamilton爵士作为一个悬赏问题而提出。TSP有着明显的实际意义, 如邮局里负责到各信箱开箱取信的邮递员, 以及去各分局送邮件的汽车等, 都会遇到类似的问题。有趣的是, 还有一些问题表面上看似乎与TSP无关, 而实质上却可以归结为TSP来求解。

若各顶点间的距离为 \(d_{ij}\) 已知。设

\[x_{ij}= \begin{cases}1, & \text { 若 }(i, j) \text { 在回路路径上} \\ 0, & \text { 其他 }\end{cases}
\]

则经典的TSP可写为如下的 数学规划模型:

\[\begin{aligned}
& \min Z=\sum_{i=1}^n \sum_{j=1}^n d_{i j} x_{i j} \\
& \text { s.t }\left\{\begin{array}{lr}
\sum_{j=1}^n x_{i j}=1, & i \in V \\
\sum_{i=1}^n x_{i j}=1, & j \in V \\
\sum_{j=s} \sum_{j \in s} x_{i j} \leq|s|-1, & \forall S \subset V, 2 \leq|s| \leq n-1 \\
x_{i j} \in\{0,1\} &
\end{array}\right.
\end{aligned}
\]

模型中，\(|V|\) 为集合中所含图的顶点数。前两个意味着对每个点而言，仅有一条边进和一条边出；第三个约束则保证了没有任何子回路解的产生。当 \(d_{ij}=d_{ji}(i,j \in V)\) 时，问题被称为对称型 TSP, 否则称为非对称型 TSP。若对所有 \(1 \leq i,j,k \leq n\), 有不等式 \(d_{i j}+d_{j k} \geq d_{i k}\) 成 立, 则问题被称为是满足三角形不等式的，简称为 \(\Delta\) TSP。

二、TSP问题的R求解

R语言中有专门处理TSP问题的包TSP，可直接调用其核心函数solve_TSP( )进行求解。其使用格式如下：

sovle_TSP(x,method,control)
#x为处理TSP问题的数据格式，method为所采用的求解方法，这里内置了十多种启发式、半启发式算法可供选择。

假设现要求一个从北京出发游遍全国34个省级行政中心的最少路线规划问题，其经纬度见下表，我们用R中的TSP包对该问题求解。

area 沈阳 长春 哈尔滨 北京 天津 呼和浩特 银川 太原 石家庄 济南 郑州 西安
longitude 123.429092 125.324501 126.642464 116.405289 117.190186 111.75199 106.23248 112.549248 114.502464 117.000923 113.665413 108.948021
latitude 41.796768 43.886841 45.756966 39.904987 39.125595 40.84149 38.48644 37.857014 38.045475 36.675808 34.757977 34.263161
area 武汉 南京 合肥 上海 长沙 南昌 杭州 福州 广州 台北 海口 南宁
longitude 114.298569 118.76741 117.283043 121.472641 112.982277 115.892151 120.15358 119.306236 113.28064 121.520076 110.19989 108.320007
latitude 30.584354 32.041546 31.861191 31.231707 28.19409 28.676493 30.287458 26.075302 23.125177 25.030724 20.04422 22.82402
area 重庆 昆明 贵阳 成都 兰州 西宁 拉萨 乌鲁木齐 香港 澳门
longitude 106.504959 102.71225 106.713478 104.065735 103.83417 101.77782 91.1145 87.61688 114.16546 113.54913
latitude 29.533155 25.040609 26.578342 30.659462 36.06138 36.61729 29.64415 43.82663 22.27534 22.19875 
#加载所需要的包
library(TSP)
library(maps)
library(maptools)
library(openxlsx)
library(mapdata)

#读取34个省级中心的经纬度数据
pr<-read.xlsx("city.xlsx")
#计算两点之间的球面距离
f_dis<-function(x,y){
  r=6371
  x=x*pi/180;y=y*pi/180
  a=c(cos(x[2])*cos(x[1]),cos(x[2])*sin(x[1]),sin(x[2]))
  b=c(cos(y[2])*cos(y[1]),cos(y[2])*sin(y[1]),sin(y[2]))
  cosg=sum(a*b)/sqrt(sum(a^2)*sum(b^2))
  dis=r*acos(cosg)
}
k<-cbind(pr$longitude,pr$latitude)
#计算34个城市的两两距离
dis_mat<-matrix(NA,34,34)
for (i in 1:34){
  for(j in 1:34){
    dis_mat[i,j]=f_dis(k[i,],k[j,])
  }
}
colnames(dis_mat)<-rownames(dis_mat)<-pr[,1]

#TSP问题求解
tsp<-TSP(dis_mat)
tour<-solve_TSP(tsp,method="2-opt")
#数字路线
path<-as.integer(tour)
#总长度
tour_length(tsp,tour)
#在地图上标识
map("china", col = "red4", ylim = c(18, 54), panel.first = grid())
map.axes()
title('中国城市')

attach(tsp_map)
points(c(longitude,longitude[1]),c(latitude,latitude[1]),
       col=2,pch=20,type="o")
pointLabel(longitude,latitude,area,
           col="blue",cex=0.74)
detach(tsp_map)

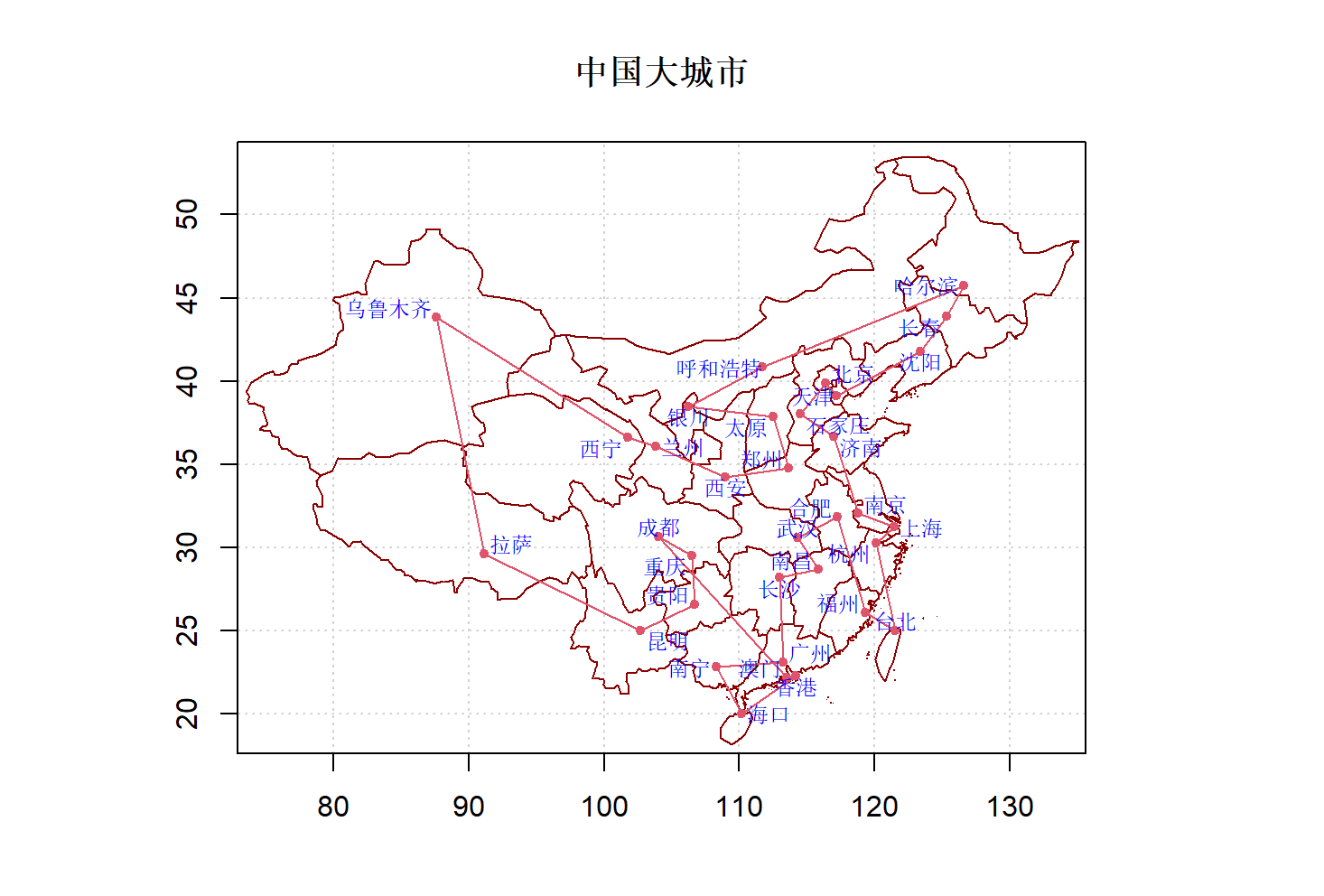
在多次运行上述代码后，我们可以从众多解中选取一个最优解为 16796.48千米，最佳路线为（ "北京" "哈尔滨" "长春" "沈阳" "天津" "济南" "郑州" "西安" "太原" "石家庄" "呼和浩特" "银川" "兰州" "西宁" "乌鲁木齐" "拉萨" "成都" "重庆" "贵阳" "昆明" "南宁" "海口" "澳门" "香港" "广州" "长沙" "南昌" "武汉" "合肥" "南京" "上海" "杭州" "福州" "台北" ）。利用maps和maptool包可将路线展现在地图上：

参考文献

  1. R语言与优化模型（三）：图与网络优化
  2. 模型 优化模型38 旅行商问题(TSP)及Python求解
  3. 中国各省会城市经纬度数据