符号扩展

在计算机算术运算中，有时必须将采用给定位数表示的数转换成具有更多位数的某种表示形式。例如，某个程序需要将一个8位数与另外一个32位数相加。要想得到正确的结果，在将8位数与32位数相加之前，必须将8位数转换成32位数形式，这个过程称为“符号扩展”。

对于正数的符号扩展非常简单，原有形式的符号位移动到新形式的符号位上，新表示形式的所有附加位都用“0”进行填充。
对于负数的符号扩展方法则根据机器数的不同而不同。

• 原码表示负数的符号扩展方法与正数相同，只不过此时符号位为“1”而已。
• 补码表示负数的扩展方法是：原有形式的符号位移动到新形式的符号位上，新表示形式的所有附加位都用“1”进行填充。

加法和减法运算

计算机在进行算术运算时，需要指出小数点的位置。根据小数点的位置是否固定，在计算机中有两种数据格式：定点表示和浮点表示。

为了避免出现误会，在给出一个数的同时就必须指明这个数的数制。例如，(1010)₂、(1010)₈、(1010)₁₀、(1010)₁₆所代表的数值就不同。除了用下标来表示不同的数制以外，在计算机中还常用后缀字母来表示不同的数制。后缀B表示这个数是二进制数（Binary）；后缀Q表示这个数是八进制数（Octal）（注意：在教材中仍是按O表示八进制数），本来八进制数的英文单词的第一个字母应当是O，因为字符O与数字0很容易混淆，所以常使用字符Q作为八进制数的后缀；后缀H表示这个数是十六进制数（Hexadecimal）；而后缀D表示这个数是十进制数（Decimal）。十进制数在书写时后缀D可以省略，其他进制在书写时后缀一般不可省略。

一、定点数的加减运算

事实上，在机器内部并没有小数点，只是人为约定了小数点的位置，小数点约定在数值位的最左边就是定点小数，小数点约定在数值位的最右边就是定点整数。因此，在运算过程中，可以不用考虑对应的定点数是小数还是整数，而只需关心它们的符号位和数值位即可。

（1）原码加减运算

当原码加减运算时，符号位并不参加运算，只有两数的绝对值参加运算。首先要判断参加运算的两个操作数的符号，再根据要求决定进行相加还是相减操作，最后还要根据两个操作数绝对值的大小决定结果的符号。

原码运算时，用 $\left| X \right| + {\left[ {\left| Y \right|} \right]_{变补}}$ 来代替 $\left| X \right| - \left| Y \right|$

注：变补是指所有的二进制数各位变反（连同符号位一起变反）后最低位加1

原码加减运算规则

1. 参加运算的操作数取其绝对值。
2. 若做加法运算，则两数直接相加；若做减法运算，则将减数先变一次补，再进行加法操作。
3. 运算之后，可能有两种情况：
   • 有进位，结果为正，即得到正确的结果。
   • 无进位，结果为负，则应再变一次补，才能得到正确的结果。
4. 结果加上符号位。

例如：在二进制形式下，首先计算7D加上6D，然后计算7D减去6D。跟十进制加减法一致，二进制加法从右到左进位。

1. $7+6$

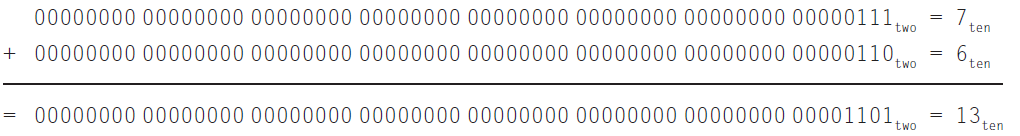
2. $7-6$

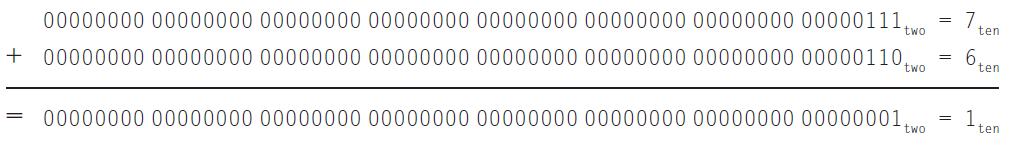
或者通过加上 $-6$ 的二进制补码来实现

（2）补码加减运算

1.补码加法

两个补码表示的数相加，符号位参加运算，且两数和的补码等于两数补码之和，即：${\left[ {X + Y} \right]_补} = {[X]_补} + {[Y]_补}$。

2.补码减法

由补码加法公式可以推出：${\left[ {X - Y} \right]_补} = {\left[ {X + ( - Y)} \right]_补} = {[X]_补} + {[ - Y]_补}$。

不管 $Y$ 的真值为正或为负，已知 ${[Y]_补}$ 求 ${[ - Y]_补}$ 的方法是：将 ${[Y]_补}$ 连同符号位一起求反，末尾加1（在定点小数中这个“1”实际上是 ${2^{-n}}$ ）。

3.补码加减运算规则

1. 参加运算的两个操作数均用补码表示。
2. 符号位作为数的一部分参加运算。
3. 若做加法运算，则两数直接相加；若做减法运算，则将被减数与减数的机器负数相加。
4. 运算结果仍用补码表示。

二、定点数的加减运算

1.定点乘法运算

乘法运算由累加和右移操作实现，可分为原码一位乘法和补码一位乘法。

当然考试的时候如果只要求直接写出结果，可以采用类似十进制乘法的方法，见下面的例子：

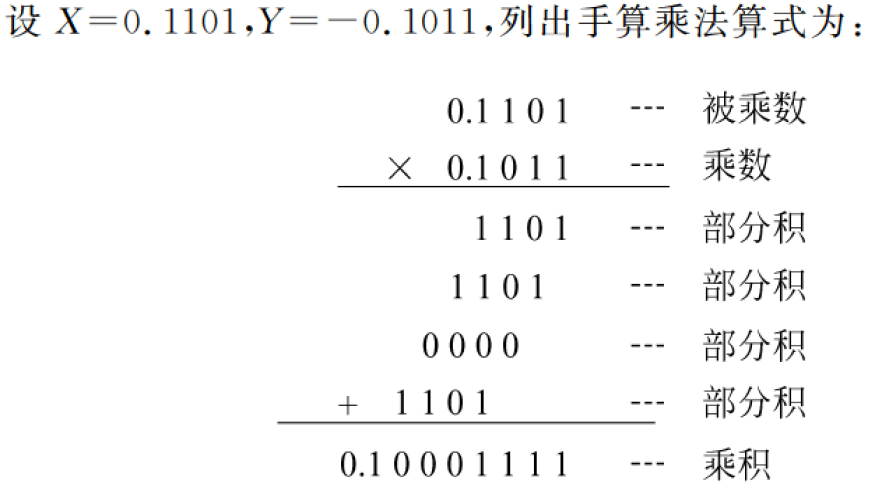
（1）原码一位乘法

原码一位乘法的特点是符号位与数值位是分开求的，乘积符号由两个数的符号位“异或”形成，而乘积的数值部分则是两个数的绝对值相乘之积。

原码一位乘法的规则为：

1. 参加运算的操作数取其绝对值。
2. 令乘数的最低位为判断位，若为1，加被乘数；若为0，不加被乘数（加 0）。
3. 累加后的部分积以及乘数右移一位。
4. 重复 $n$ 次2和3。
5. 符号位单独处理，同号为正，异号为负。
   

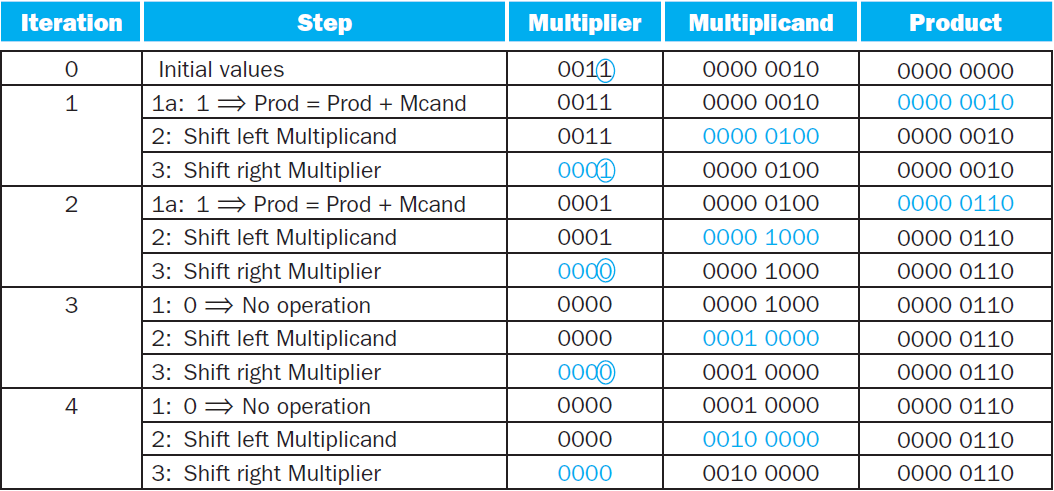
例如：使用4位长的数，计算 $2 \times 3$

三、浮点表示法

浮点表示的设计者必须在尾数（flection）位数和指数（exponent）位数之间找到折中，因为字的大小是固定的，这意味着有一部分增加一位，另一部分就要减少一位。浮点数表示法是指以适当的形式将比例因子表示在数据中，让小数点的位置根据需要而浮动。

1.浮点数的表示格式

通常、浮点数表示为 $N = {( - 1)^S} \times F \times {2^E}$，式中，$S$ 取值0或1，用来决定浮点数的符号；$F$ 为小数（尾数）字段的值；$E$ 为指数字段的值。

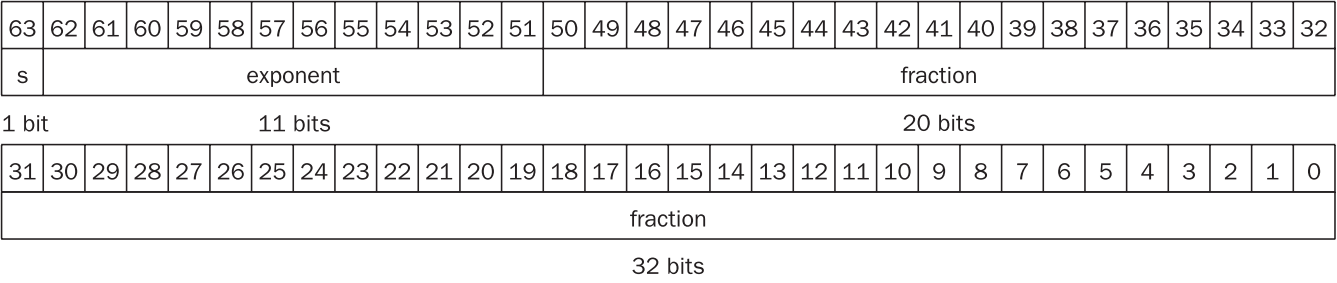
LEGv8的浮点数（floating-point number）表示如下：

和整数算术运算一样，浮点算术运算中也会产生溢出中断。注意，这里的溢出（overflow） 。意味着指数太大而超过了指数字段的表示范围。为了和上溢区分开来，我们将其称为下溢（underflow） 。下溢发生的条件是负的指数太大而不能在指数字段中表示出来。

一种减少上溢和下溢的方法是采用另一种格式，使得指数更大。基于 double 的操作称为双精度 (double precision) 浮点运算；之前的格式称为单精度 (single precision) 浮点运算。

2.IEEE 754浮点标准

为了能打包更多的数据位， IEEE 754 隐藏了规格化二进制数小数点前面的1。因此，在单精度下，数据有 $24$ 位（隐含的 $1$ 和 $23$ 位尾数），在双精度下为 $53$ 位（ $1+52$ ) 。

IEEE 754 规定单精度的偏差为 $127$，双精度的指数偏差为 $1023$，带偏差的指数意味着浮点数表示的值实际为：

$N = {( - 1)^S} \times (1 + {尾数}) \times {2^{({指数} - {偏差})}}$

例如：将100.25转换成单精度浮点数格式。

• 将十进制数转换成二进制数。

 $0110 0100.01B$

• 规格化二进制数。

$0110 0100.01=1.$10010001 $\times {2^6}$

• 计算出阶码的移码（偏移值+阶码真值）
  • 对于单精度浮点数，偏移值是127（0111 1111）
  • 阶码真值在这题为6（见公式中2的次方数）

移码表示的阶码为：$127（0111 1111）+6（0110）= 133$（1000 0101）

• 以相应的浮点数格式存储，在这里是单精度浮点数，所以：