地震储层预测笔记—AVO近似公式总结

(一).Zeoppritz方程

AVO地球物理基础是平面弹性波在层状介质下推倒得出的Zeopprizt方程，在两层介质下（如图1所示）其Zeopprizt方程可以写成（式1）：

其中P波入射角\(\theta_{1}\)（其反射角相同），反射转换S波反射角\(\phi_{1}\)，透射P波的透射角\(\theta_{2}\)，及S波透射角\(\phi_{2}\)，在各向同性介质下满足Snell定律：

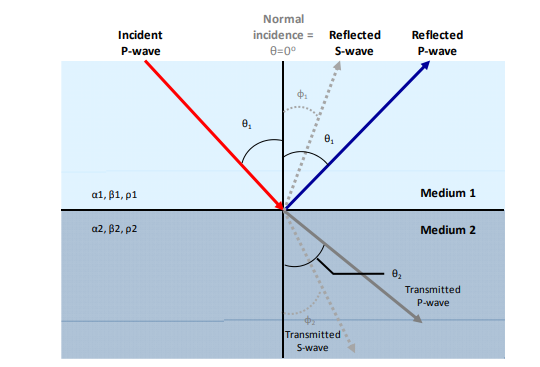
​ 图1 P波入射时，在两层分界面处其反射波与折射波示意图

在应用时，我们一般使用Zoeppritz 方程的线性近似公式，进行AVO反演，反演储层的弹性公式，进而结合岩石物理学统计规律，用于储层的岩性分析和油气预测，在本笔记中，将各种常用的AVO近似公式进行简单总结，其介质假设为均匀层状各向同性介质.

(二).Zeoppritz方程的AVO近似公式

A. Aki-Richards近似公式（Richards-Frasier近似公式）

​ Richards、Frashiser(1976)和Aki、Richards(1980)推导出反射P波的反射系数公式，其包括三项，第一项包含密度，第二项包含P波速度，第三项包含S波速度。其表达式：

其中

将式（3）中的角度项提取，可以将式（3）可以写为：

式（5）其也被Wiggens简化成一个横波和纵波反射率的表达式，首先，假设横波和纵波速度比：

在小角度假设的情况下，忽略第三项，其变化成：

在此，令纵波反射率和横波反射率，为\(R_{p}\)和\(R_{s}\)为如下:

将式（8）带入式（7）可以化简为两项式：

令

由此得到得到斜率-截距表达式：

B.Shuey 近似表达式

​ 在上Aki-Richard公式中，其包括三项：纵波速度、横波速度、密度三项，Shuey（1985）发表了另一种关于Zoeppritz方程近似表达式其中包括纵波速度，密度和泊松比，式如下：

其中：

式（12）也可以被写作为如下表达式B：

其中

对于小角度范围限制后，对式（15）可以进行线性化处理，忽略第三项，其式可以写成

在式(17)中，\(R_{p}\)是法向反射率，\(B\)是梯度，其角度的准确范围在25到30度，其近似公式是准确的。

在假设密度对AVO效应的影响是忽略不计，Bortfeld’s近似表达式可以形成Shuey近似表达式，如下式：

其中\(I\)是声波阻抗，\(\mu\)是剪切模量。 由此，Shuey（1985）将上式（12）可以改写为三项式如下式：

其中：

其中\(\alpha,\beta,\rho\)分别为纵波速度、横波速度、密度，其中\(\sigma\)为介质的泊松比，其中\(\gamma\)为横纵波速比。

C. Verm and Hilterman 近似表达式

Hilterman（1990)加入一些简化条件，进而简化Shuey‘s公式，其简化条件如下：

1. 假设纵横波速比\(V_p/V_s=2\), 并且假设泊松比\(v=1/3\) ,并且\(A_{0}=-1\)。

2. 假设角度范围为小角度假设\(\theta<30\),进而得到正弦假设 \(\tan ^2 \theta \cong \sin ^2 \theta\)。

   由此，可以得到，将式（12）可以写成如下形式：

   \[R(\theta)=R_p\left(1-\sin ^2 \theta\right)+\frac{9}{4} \Delta v \sin ^2 \theta \tag{21}
   \]

   或者改写为：

   \[R(\theta)=R_P \cos ^2 \theta+2.25 \Delta v \sin ^2 \theta \tag{22}
   \]

   在式(21)或者式（22）中，\(R_{p}\)控制小角度范围，其中\(\Delta v\)控制大角度范围，近道（near-offset）道集信息可以利用该式可以进行P波阻抗成像，远道（far-offset)道集信息可以进行泊松比成像，Possion比的反射率可以指示岩性和流体性质变化。将其化简为截距-斜率公式，其可以表示为

   \[\begin{aligned}
   R(\theta) & =R_P \cos ^2 \theta+\frac{9}{4} \Delta \sigma \sin ^2 \theta \\
   & =R_P+\left[\frac{9}{4} \Delta \sigma-R_P\right] \sin ^2 \theta \\
   & =R_P+G \sin ^2 \theta
   \end{aligned} \tag{23}
   \]

   由此，从式（23）可以得到通过最小二乘拟合算法，计算获得截距\(R_{p}\)和斜率\(G\) ，由此可以计算得到两层泊松比差，计算式如下:

   \[\Delta \sigma=4 / 9\left(R_P+G\right) \tag{24}
   \]

D. Smith 和 Gidlow近似公式

Smith 和 Gidlow（2003）将Aki-Richard AVO近似表达式进行重新排列，并利用Gardner’s速度与密度的经验公式，通过速度变化率替换密度变换率，简化Aki-Richard公式，并引入了流体因子项，第一步：首先将Aki-Richard方程进行重新排列：

将式（25）重新写为：

利用Gardner‘s速度与密度经验公式：

对式（27）的两边求微分，建立其速度与密度的微分关系：

将式（28）代入式（26）中：

其中

当其被应用于动校正校正后的CMP道集，公式(29)可以通过最小二乘法求解。其可以将加权叠加道集。其权重值是依赖于入射角（也可以是偏移距和双程旅行时），推导出纵横波速度比。然后推导出权重乘道集并相加，得到加权叠加道集。通过加权叠加道集可以推导出零偏移距纵波速度反射率和零偏移距横波速度反射率。在此基础上，Smith和 Gidlow（1987）介绍了另外两种AVO属性：

​ （1）伪泊松比反射率，其AVO属性定义为：

​ (2) 流体因子，Smith和Gidlow(1987)采用了Castagna’s-Murdrock 纵波速度与横波速度的经验公式：

对式（33）的两端，求取微分：

该公式应用于湿润饱和的储层介质，其湿润饱和的情况由储层被流体填充或者烃源岩（非弹性），Smith和Gidlow定义为流体因子：

E. Fatti‘s 近似公式

在上述Smith和Gidlow公式中，其选用了Gardner’s公式，但其不一定适用于一些特殊情况，这是Fatti’s公式其被考虑，其通过Aki-Richards公式被写成：

通过该公式通过求解得到纵波波阻抗反射率和横波波阻抗反射率，在小角度假设下，其\(sin(\theta)\cong tan(\theta)\) ,其第三项被忽略，变成下式：

其中在该近似公式没做\(V_{p}/V_{s}\)或者密度\(\rho\) 的前提假设，该公式对于大角度，有较好的反映。

F. Lame参数提取提取

GoodWay分别在1997年和2001年，提出利用Lame-弹性系数来代替纵横波速度或者阻抗，提供了两种不同反映流体性质的AVO属性，Lambda-rho（\(\lambda-\rho\)）和mu-rho(\(\mu-\rho\))属性，去反映岩石的岩性及流体性质。其推倒如下：

以及

由此

和

因此可以推导出：

G. Xu and Bancroft extraction AVO近似公式

Xu和Bancroft （1998）通过对Aki和Richard的AVO近似表达式变形推导，直接提取从叠前道集提取Lame系数。其近似公式写成不可压缩性系数（incompressibility Coefficient）\(\lambda\) 和剪切模量（Shear modulus）\(\mu\) 以及密度（density）\(\rho\) 的组合：

或者其也可以写成关于体积模量（Bulk Modulus）\(k\)的表达式：

其在小角度假设情况下，将第三项表达式进行忽略，其密度项将被忽略。如果密度项需要被考虑，其可以利用Gardner公式，推动出下式稳定的线性表达式：

其对储层的岩性与流体性质预测有较好的帮助。

H. Gray et al. extraction 和Russell et al. AVO近似表达式

Gray et al.(1999)在Aki and Richards AVO 近似表达式的基础上，推导一个关于剪切模量\(\mu\)，体积模量\(k\) ,密度\(\rho\) 的表达式：

其中，Russell et al.(2011)得到的AVO近式表达式，如下式：

(三).AVO属性提取分析

由上述可知，Smith和Gidlow AVO公式与梯度反演的一致性，在上述两个部分，推导近似公式，其在小角度假设下，可以推导出AVO两项式：

其中截距项\(R_{p}\) 为纵波阻抗；

其中\(G=R_{p}-2R_{s}\)为梯度项：

在Smith和Gidlow近似公式中，其储层的弹性参数\(\Delta \beta / \beta\)和\(\Delta \alpha /\alpha\) 是可以被估计的，然而，Smith和Gidlow，其利用Gardner密度经验公式，但两者是等价的：

其化简为：

其下一步，推导横波阻抗反射率\(R_{s}\) ,其得到：

同上，将其推导出：

由此，可以总结出\(\Delta \beta / \beta\)和\(\Delta \alpha /\alpha\) 可以通过\(R_{p}\) 和\(G\) 的线性组合得到。由此，可以推导出伪泊松反射率的\(R_{p}\) 和\(G\) 的线性组合：

最后，我们将推导出流体因子\(F\) 在假设\(\beta /\alpha=1/2\) :

由上可知，通过这些AVO属性的表示可以表示AVO二项式中梯度\(G\) 和AVO截距\(R_{p}\) 线性组合：

​ 表一：AVO反射率属性由AVO二项式截距项与梯度项的线性组合系数与物理假设条件分析

​