11.1
CF449D Jzzhu and Numbers
题目分析:
考虑直接算的话就相当于限制每一位必须有一个 \(0\),显然不如反着来,也就是某一位必须全为 \(1\),也就是我们计算与之后不为 \(0\) 的方案,用总的方案数也就是 \(2^n\) 减一下就好了。
我们可以观察到数据范围里很怪的一点:\(a_i \le 10^6\),这也就提示我们可以按位来考虑。
具体来说就是可以设 \(dp[S]\) 表示我们选择含有 \(S\) 这些 \(1\) 的数的个数,严谨一点就是求解 \(\sum_{i=1}^n [a_i \& S = S]\),这显然可以每个数对它对应的数做贡献,然后做一遍高维后缀和就好了。
我们最终的答案难道就是所有的 \(S\) 求个和嘛?显然不是啊。
因为我们要求的其实是第一位为 \(1\) 或 第二位为 \(1\) 或 \(\cdots\)。
发现可以容斥啊,其实就是 \(S\) 中含有奇数个 \(1\) 的加上,含有偶数个 \(1\) 的减去,然后就结束了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
const int MOD = 1e9+7;
int f[1<<22],a[N],pre[N];
int mod(int x){
return ((x % MOD)+MOD)%MOD;
}
signed main(){
int n;
scanf("%lld",&n);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]),f[a[i]]++;
for(int j=0; j<20; j++){ //高维后缀和
for(int i=1; i<(1<<20); i++)
if((i >> j) & 1){
f[i ^ (1<<j)] = mod(f[i ^ (1<<j)] + f[i]);
}
}
pre[0] = 1;
for(int i=1; i<=n; i++) pre[i] = mod(pre[i-1] * 2); //pre[i] = 2^i,方便计算答案
int ans = pre[n] - 1; //因为必须选择一个,所有去掉全部不选的情况
for(int i=1; i<(1<<20); i++){
int cnt = __builtin_popcount(i);
if(cnt & 1) ans = mod(ans - (pre[f[i]] - 1)); //因为是求的 ans - 方案数,所以奇数是减
else ans = mod(ans + (pre[f[i]] - 1));
}
printf("%lld\n",ans);
return 0;
}
CF932E Team Work
题目分析:
先稍微说一下第二类斯特林数吧。
第二类斯特林数就是 \(S_n^m\) 表示将 \(n\) 个不同的小球放到 \(m\) 个相同的盒子里的方案数,也可以记作 \(\begin{Bmatrix} n \\ m\end{Bmatrix}\)
递推式的就是 \(\begin{Bmatrix} n \\ m \end{Bmatrix} = \begin{Bmatrix} n-1 \\ m-1 \end{Bmatrix} + m \times \begin{Bmatrix} n-1 \\ m \end{Bmatrix}\),其实就是可以理解为枚举最后一个小球是否单独开一个盒子,不单独开的式子是因为小球是不同的所以放到不同的盒子算作不同的方案所以要乘以 \(m\)。
下面其实才是常用的点,一个性质:
\]
感觉本题的推导也很有用,包含了很多技巧。
&\sum_{i=1}^n \binom{n}{i} \times i^k \\
&= \sum_{i=0}^n \binom{n}{i} \times i^k \\
&= \sum_{i=0}^n \dfrac{n!}{i!(n-i)!} \sum_{j=0}^k \begin{Bmatrix} k \\ j \end{Bmatrix} \times \binom{i}{j} \times j! \\
&= \sum_{i=0}^n \dfrac{n!}{(n - i)!} \sum_{j=0}^k \begin{Bmatrix} k \\ j \end{Bmatrix} \times \dfrac{1}{(i-j)!} \\
&= \sum_{i=0}^n \sum_{j=0}^k \begin{Bmatrix} k \\ j \end{Bmatrix} \dfrac{n!}{(n-i)!(i-j)!} \\
&= \sum_{i=0}^n \begin{Bmatrix} k \\ j \end{Bmatrix} \sum_{i=0}^n \dfrac{(n-j)!}{(n-i)!(i-j)!} \times \dfrac{n!}{(n - j)!} \\
&= \sum_{j=0}^k \begin{Bmatrix} k \\ j \end{Bmatrix} \dfrac{n!}{(n-j)!} \sum_{i=0}^n \binom{n-j}{n-i} \\
&= \sum_{j=0}^k \begin{Bmatrix} k \\ j \end{Bmatrix} \dfrac{n!}{(n-j)!}2^{n-j}
\end{aligned}
\]
然后直接预处理一下第二类斯特林数就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int N = 5005;
int S[N][N];
int mod(int x){
return x % MOD;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
void pre_work(int mx){
S[0][0] = 1;
for(int i=1; i<=mx; i++){
for(int j=1; j<=i; j++){
S[i][j] = mod(S[i-1][j-1] + mod(j * S[i-1][j]));
}
}
}
signed main(){
int n,k;
scanf("%lld%lld",&n,&k);
pre_work(k);
int ans = 0,tmp1 = 1,tmp2 = power(2,n),inv2 = power(2,MOD-2);
for(int i=0; i<=k; i++){
ans = mod(ans + mod(mod(S[k][i] * tmp1) * tmp2));
tmp1 = mod(tmp1 * (n - i));
tmp2 = mod(tmp2 * inv2);
}
printf("%lld\n",ans);
return 0;
}
CF1485F Copy or Prefix Sum
题目分析:
注意我们是给定 \(b\) 填 \(a\) 别被绕晕了。
我们考虑假设我们已经填完到了第 \(i\) 位且前 \(i-1\) 位和为 \(S\),那么我们这一位可以填什么。
显然只有两个值对应两种性质:\(b_i、b_i - S\)。
那么我们就可以考虑设 \(dp[i]\) 表示和为 \(i\) 的方案,省略第一维前多少位。
那么转移就是:
\sum_{j = -\infty}^{+\infty} dp[j] \to dp[b[i]]
\]
第一个转移就相当于一个偏移,第二个转移就相当于一个加全局和,都是很好弄的。
但是需要注意当上面的两个值相等,也就是 \(S = 0\) 时,一个转移就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
const int MOD = 1e9+7;
int a[N];
signed main(){
int t;
scanf("%lld",&t);
while(t--){
int n;
scanf("%lld",&n);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
map<int,int> f;
int ans = 1,sum = 0; //记录偏移量
f[0] = 1;
for(int i=1; i<=n; i++){
int tmp = f[sum];f[sum] = ans;sum -= a[i];
ans = ((ans + ans - tmp)%MOD+MOD)%MOD;
}
printf("%lld\n",ans);
}
return 0;
}
11.2
CF1628D2 Game on Sum (Hard Version)
题目分析:
显然可以考虑设 \(dp[i][j]\) 表示前 \(i\) 次操作 \(Bob\) 选择了 \(j\) 次加的最终的答案。
那么假设 \(Alice\) 选择 \(t\) 的话,转移方程就是:
\]
可以发现我们睿智的 \(Alice\) 一定会选择 \(t = \dfrac{dp[i-1][j] + dp[i-1][j-1]}{2}\),可以证明如果比这个值大或者比这个值小都不是最优的。
\(dp\) 初值就显然是 \(dp[i][i] = i \times k,dp[i][0] = 0\)。
我们考虑对于这个式子其实就相当于 \(dp[i][j]\) 会对 \(dp[i+1][j]\) 和 \(dp[i+1][j+1]\) 产生 \(\dfrac{dp[i][j]}{2}\) 的贡献,那么就考虑每一个 \(dp[i][i]\) 对 \(dp[n][m]\) 的贡献就好了,显然 \(Bob\) 最多会选择 \(m\) 次加。
我们考虑转化一下其实就是相当于从 \((i,i)\) 走到 \((n,m)\) 的方案数就是它的贡献次数,但是从 \((i,i)\) 走到 \((i+1,i+1)\) 是显然没有意义的,因为 \((i+1,i+1)\) 就是一个初值,所以就是可以理解为从 \((i+1,i)\) 走到 \((n,m)\) 的方案数,其实就是 \(n - i - 1\) 步里选 \(m-i\) 步向上,就是 \(\binom{n-i-1}{m-i}\),但是我们每一步都会造成贡献除二,显然我们总共走了 \(n-i\) 步,因为我们第一次走的也算一步,所以答案也要除以 \(2^{n-i}\),所以最终就是:
\]
那么直接暴力算这个式子的值就好了。
但是需要特判 \(n=m\) 的情况,因为我们把这个当作了初值,所以不会去处理。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
const int MOD = 1e9+7;
int fac[N],inv[N],pw[N];
int mod(int x){
return x % MOD;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
void pre(int mx){
fac[0] = 1;
for(int i=1; i<=mx; i++) fac[i] = mod(fac[i-1] * i);
inv[mx] = power(fac[mx],MOD-2);
for(int i=mx-1; i>=0; i--) inv[i] = mod(inv[i+1] * (i + 1));
int inv2 = power(2,MOD-2);
pw[0] = 1;
for(int i=1; i<=mx; i++) pw[i] = mod(pw[i-1] * inv2);
}
int C(int n,int m){
if(n < m) return 0;
return mod(mod(fac[n] * inv[m]) * inv[n - m]);
}
signed main(){
pre(1000000);
int t;
scanf("%lld",&t);
while(t--){
int n,m,k;
scanf("%lld%lld%lld",&n,&m,&k);
int ans = 0;
for(int i=1; i<=m; i++){
ans = mod(ans + mod(mod(mod(k * i) * C(n-i-1,m-i)) * pw[n-i]));
}
if(n == m) ans = mod(k * m);
printf("%lld\n",ans);
}
return 0;
}
CF1499E Chaotic Merge
题目分析:
我们发现如果我们要求的是整个字符串的答案的话可以轻松地 \(dp\) 解决。
也就是设 \(dp[i][j][0/1]\) 表示使用了 \(x\) 的前 \(i\) 个和 \(y\) 的前 \(j\) 个,最后一个选择的是 \(y\) 或 \(x\) 的合法方案数。
这样可以根据 \(dp\) 值就很轻松地将右端点的问题解决了,但是左端点的移动怎么办呢?
我们会发现对于不同的左端点其对于 \(dp\) 值的影响只在于初值,所以我们对于每一个位置都赋一个初值然后去 \(dp\) 就好了。
但是这样又出现了一个问题,对于题目中式子的一个隐藏条件:\(|x|,|y| \ge 1\),所以这样之后会发生对于 \(i\) 他可能是 \(j\) 来说合法的右端点但不一定是 \(k\) 来说合法的右端点,所以直接对 \(dp\) 值求和就会出问题,因为会发现 \(|x| = 0\) 或 \(|y| = 0\) 的情况。
我们就考虑再记一维这一维是一个二进制状态第一位代表是否选择过 \(x\),第二位代表是否选择过 \(y\),这样统计就很简单了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e3+5;
const int MOD = 998244353;
char x[N],y[N];
int dp[N][N][2][4];
void add(int &x,int y){
x = (x + y)%MOD;
}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
scanf("%s%s",x+1,y+1);
int n = strlen(x+1);
int m = strlen(y+1);
for(int i=0; i<=n; i++){
for(int j=0; j<=m; j++){
if(i < n) add(dp[i+1][j][1][1],1);
if(j < m) add(dp[i][j+1][0][2],1);
for(int s=0; s<4; s++){
if(i < n && x[i+1] != x[i]) add(dp[i+1][j][1][s | 1],dp[i][j][1][s]);
if(j < m && y[j+1] != x[i]) add(dp[i][j+1][0][s | 2],dp[i][j][1][s]);
if(i < n && x[i+1] != y[j]) add(dp[i+1][j][1][s | 1],dp[i][j][0][s]);
if(j < m && y[j+1] != y[j]) add(dp[i][j+1][0][s | 2],dp[i][j][0][s]);
}
}
}
int ans = 0;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
add(ans,dp[i][j][0][3] + dp[i][j][1][3]);
}
}
printf("%lld\n",ans);
return 0;
}
CF1109D Sasha and Interesting Fact from Graph Theory
题目分析:
我们可以考虑拆分问题,把问题看作两个步骤:
- 构造出 \(a,b\) 间的路径
- 将其他点挂到这个路径上,形成一棵树
对于这个数据范围显然可以考虑直接枚举链上点的个数,设为 \(i\),那么对于选择路径的方案数就是 \(\binom{n-2}{i-2} \times (i-2)! \times \binom{m-1}{i-2}\)。
具体解释一下:因为 \(a,b\) 必选,所以我们可以操作的点其实就少了两个,因为 \(i-2\) 个点可以任意排列且不同的排列属于不同的方案所以要乘以一个阶乘,然后最后就是将 \(m\) 的权值分给 \(i-1\) 条边,经典的插板法应用。
然后把其余的点挂到路径上就是广义 Cayley 定理啦,也就是 \(i \times n^{n - i - 1}\)
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
const int MOD = 1e9+7;
int fac[N],inv[N];
int mod(int x){
return x % MOD;
}
int power(int a,int b){
b = (b + MOD-1)%(MOD-1); //会离谱的出现负数,所以就考虑欧拉定理
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
void pre_work(int mx){
fac[0] = 1;
for(int i=1; i<=mx; i++) fac[i] = mod(fac[i-1] * i);
inv[mx] = power(fac[mx],MOD-2);
for(int i=mx-1; i>=0; i--) inv[i] = mod(inv[i+1] * (i + 1));
}
int C(int n,int m){
if(n < m) return 0;
return mod(fac[n] * mod(inv[m] * inv[n-m]));
}
signed main(){
pre_work(1000000);
int n,m; //a,b 形如空谈
scanf("%lld%lld",&n,&m);
int ans = 0;
for(int i=2; i<=min(n,m+1); i++){ //枚举链上有多少个点,显然最多就是 m + 1 了。
int P1 = mod(i * power(n,n - i - 1)); //把剩下的点挂到链上
int P2 = C(m-1,i-2); //把权值 m 分配到 i-1 条边上
int P3 = fac[i-2]; //这几个点可以任意排列
int P4 = C(n-2,i-2); //这几个点可以任选
int P5 = power(m,n - i); //剩下的边的权值可以随意赋
ans = mod(ans + mod(P1 * mod(P2 * mod(P3 * mod(P4 * P5)))));
}
printf("%lld\n",ans);
return 0;
}
11.3
CF856C Eleventh Birthday
题目分析:
显然可以发现一点,题目中的条件可以转化为偶数位上的数与奇数位上的数大小相同。
我们可以发现对于奇数位和偶数位的数对于答案的影响是不同的,所以可以考虑分开处理。
可以考虑设 \(f[i][j][k]\) 表示前 \(i\) 个奇数位的数,有 \(j\) 个的开头在偶数位上,对结果的贡献为 \(k\) 的方案数。
注意:这里的方案数只是指的我们顺次安排偶数位的结果,对于剩下的一些奇数位可能是空余的,不过不要紧。
也同理可以设 \(g[i][j][k]\) 表示前 \(i\) 个偶数位的数,有 \(j\) 个的开头在偶数位上,对结果的贡献为 \(k\) 的方案数。
转移其实就很简单了,就是枚举当前这个数在偶数位还是奇数位,我们记 \(a[i]\) 代表第 \(i\) 个奇数位的数对答案的贡献,\(b[i]\) 代表第 \(i\) 个偶数位的数对答案的贡献:
g[i][j][k] = g[i-1][j][k - b[i]] + f[i-1][j-1][k + b[i]]
\]
也可以显然发现一点,这样转移出来对于 \(f\) 来说,有用的只有 \(f[n][n/2][\cdots]\),我们这里记 \(n\) 为奇数位的数的个数,\(m\) 为偶数位的数的个数。
那么我们接下来就可以考虑将这两个数组合并,可以考虑枚举偶数位 \(i\) 个数位于偶数位上对答案的贡献为 \(j\),那么我们的方案数就是:
\]
但是这个只是我们选数的方案啊,我们还需要考虑数与数之间的插入,可以发现因为任意插入偶数位的数不会改变原来存在的数的贡献,所以就可以考虑将偶数位的数插入奇数位的数内。
对于偶数位的数的这 \(i\) 个,必须位于奇数位的这 \(n - \dfrac{n}{2}\) 个数后面,而且一个数后面可以含有多个或者一个都没有,其实就是一个插板法啊。
也同理对于偶数位的剩下的 \(m-i\) 个数,必须位于奇数位的这 \(n/2\) 个数后面,也是一个插板法。
但是这个是显然不够的,因为我们会发现对于偶数位的数我们将开头在偶数位的数任意交换位置之后都是合法的且全新的一种方案,对于开头在奇数位的同理。而对于奇数位的数这个条件显然也满足,所以答案要乘以一个:
\]
虽然说了这么多,但是其实代码是很好写的。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4005;
int f[2][N][12],g[2][N][12],fac[N],C[N][N],a[N],b[N];
int mod(int x,int MOD){
return ((x % MOD)+MOD)%MOD;
}
void Add(int &x,int y){
x = (x + y) % 998244353;
}
int calc(int n,int m){
if(m == 0) return n == 0;
return C[n + m - 1][m - 1];
}
int get(int x){
if(x == 0) return 1;
int cnt = 0;
while(x){
cnt++;
x/=10;
}
return cnt;
}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%lld",&t);
fac[0] = 1;
for(int i=1; i<=2000; i++) fac[i] = mod(fac[i-1] * i,998244353);
C[0][0] = 1;
for(int i=1; i<=2000; i++){
C[i][0] = 1;
for(int j=1; j<=i; j++){
C[i][j] = mod(C[i-1][j] + C[i-1][j-1],998244353);
}
}
while(t--){
//奇数:奇数位的数 偶数:偶数位的数
int p;
int n = 0,m = 0;
scanf("%lld",&p);
for(int i=1; i<=p; i++){
int h;scanf("%lld",&h);
if(get(h) & 1) a[++n] = h % 11;
else b[++m] = h % 11;
}
//设 f[i][j][k] 表示前 i 个为奇数的数,有 j 个的开头在偶数位上,贡献为 k 的方案数
//g 就是将第一个改为了前 i 个为偶数的数
//这里是强制为每一个数选定一个他是偶数位/奇数位,具体是否合法也不一定呢
f[0][0][0] = 1;
for(int i=1; i<=n; i++){
int now = i & 1;
memset(f[now],0,sizeof(f[now]));
for(int j=0; j<=i; j++){
for(int k=0; k<=10; k++){
Add(f[now][j][k],f[now^1][j][mod(k - a[i],11)]);
if(j) Add(f[now][j][k],f[now^1][j-1][mod(k + a[i],11)]);
}
}
}
g[0][0][0] = 1;
for(int i=1; i<=m; i++){
int now = i & 1;
memset(g[now],0,sizeof(g[now]));
for(int j=0; j<=i; j++){
for(int k=0; k<=10; k++){
Add(g[now][j][k],g[now^1][j][mod(k - b[i],11)]);
if(j) Add(g[now][j][k],g[now^1][j-1][mod(k + b[i],11)]);
}
}
}
int ans = 0;
for(int i=0; i<=m; i++){ //枚举偶数有多少个在偶数位上。
for(int j=0; j<=10; j++){ //枚举偶数的贡献
Add(ans,g[m&1][i][j] * f[n&1][n/2][mod(11 - j,11)] %998244353 * fac[i] %998244353* fac[m - i] %998244353* fac[n/2] %998244353* fac[n - (n / 2)] %998244353* calc(m - i,n / 2 + 1) %998244353* calc(i,n - (n / 2)));
//m - i 个数必须放在 n/2 这些数对应的后面或第一个数前面,也就是插板法,可以为空
}
}
printf("%lld\n",ans);
for(int i=0; i<=n+1; i++) for(int j=0; j<=10; j++)f[1][i][j] = f[0][i][j] = 0;
for(int i=0; i<=m+1; i++) for(int j=0; j<=10; j++)g[1][i][j] = g[0][i][j] = 0;
}
return 0;
}
11.5
CF946F Fibonacci String Subsequences
题目分析:
可以发现,我们其实可以使用合并的思想去看这个题,就是啥意思呢。
我们在 \(F(i)\) 内的方案数,其实就是在 \(F(i-1)\) 里的方案数加在 \(F(i-2)\) 里的方案数加横跨 \(F(i-1)\) 和 \(F(i-2)\) 的方案数。
就考虑怎么做可以做到处理横跨的这种情况。
显然可以想到一个 \(dp\),就是设 \(f[i][j][k]\) 表示在 \(F(i)\) 中 \([j,k]\) 这个子串作为其某一个子序列的子串的次数。
讨论转移也是上面这个想法。
考虑全在 \(F(i-1)\) 中的怎么算,直接就是 \(f[i-1][j][k]\) 吗?显然不是。
因为多加了一个 \(F(i-2)\),所以其实对于这里面的数我们可以随便选,所以是 \(f[i-1][j][k] \times 2^{len_{i-2}}\)(这里设 \(len_i\) 代表 \(F(i)\) 的长度)吗?
因为只有当 \(k=n\) 的时候我们对于 \(F(i-2)\) 才没有什么限制,否则是有限制,所以综合就是这个式子:
\begin{cases}
f[i-1][j][k] \times 2^{len_{i-2}} &k = n \\
f[i-1][j][k] & k \not= n
\end{cases}
\]
而对于全部在 \(F(i-2)\) 中也是同理,就不多分析了,直接给出结论:
\begin{cases}
f[i-2][j][k] \times 2^{len_{i-1}} &j = 1\\
f[i-1][j][k] &j \not= 1
\end{cases}
\]
然后就是考虑跨区间的情况,其实也是很简单的:
\]
初值也非常简单啦,\(f[0][i][i] = [s[i] = 0],f[1][i][i] = [s[i] = 1]\)
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int N = 205;
int f[N][N][N],len[N],pw[N];
char s[N];
int mod(int x){
return x % MOD;
}
void add(int &x,int y){
y = mod(y);
x = mod(x + y);
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
signed main(){
int n,x;
scanf("%lld%lld",&n,&x);
scanf("%s",s+1);
len[0] = len[1] = 1;
pw[0] = 2,pw[1] = 2; //pw 直接记录对应的答案
for(int i=2; i<=x; i++){
len[i] = (len[i-1] + len[i-2]) % (MOD - 1); //卧槽??欧拉定理
pw[i] = power(2,len[i]);
}
for(int i=1; i<=n; i++){
f[0][i][i] = (s[i] == '0');
f[1][i][i] = (s[i] == '1');
}
for(int i=2; i<=x; i++){
for(int j=1; j<=n; j++){
for(int k=j; k<=n; k++){
add(f[i][j][k],f[i-1][j][k] * (k == n ? pw[i-2] : 1));
add(f[i][j][k],f[i-2][j][k] * (j == 1 ? pw[i-1] : 1));
for(int p = j; p < k; p++){
add(f[i][j][k],f[i-1][j][p] * f[i-2][p+1][k]);
}
}
}
}
printf("%lld\n",f[x][1][n]);
return 0;
}
10.6
CF295D Greg and Caves
题目分析:
我们可以发现这个洞从上大小大小就是呈现:小-大-小 的趋势,所以我们知道能知道对于其中一半的方案是什么,就可以通过乘法原理得到整体的方案数。
我们也可以发现对于中间的这个长的洞在哪里是无所谓的,只要我们确定了它的长度以及这一整个洞有多少行我们就可以确定方案数。
所以其实可以考虑直接设 \(f[i][j]\) 表示整个洞有 \(i\) 行第 \(i\) 行的长度为 \(j\),这从 \(1\) 到 \(i\) 洞的长度满足非严格单调递增。
所以转移就是显然地:
\]
为啥 \(k\) 从 \(2\) 开始?因为我们至少是有两个黑块啊。
所以会发现这个很有道理,但是不对啊。那么原因是什么?
我们考虑对于一个长度为 \(k\) 的区间难道 \(i-1\) 只有一种选择吗?显然不是,他有 \(j - k + 1\) 种选择啊,所以最终的方程就是:
\]
但是这样却会超时,很让人头大。冷静的分析一下会发现,我们假设从小到大枚举 \(j\) 那么我们每一次都是加一个前缀和,也就是 \(j \to j + 1\) 我们变化的就是 \(\sum_{k=2}^{j+1} dp[i-1][k]\),所以维护一下前缀和就好了。
那么就考虑最终的答案是什么:
\]
最后乘以一个 \(m - k + 1\) 也是同理的,因为显然不止一种方案
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int N = 2e3+5;
int n,m,f[N][N],res,g[N][N];
int mod(int x){
return x % MOD;
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=2;i<=m;i++) f[1][i]=1;
for(int i=2;i<=n;i++){
int sum = 0;
for(int j=2;j<=m;j++){
sum = mod(sum + f[i-1][j]);
f[i][j] = mod(f[i][j-1] + sum);
}
}
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
g[i][j] = mod(g[i-1][j] + f[i][j]);
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
res = mod(res + mod(mod(f[i][j] * g[n+1-i][j]) * (m - j + 1)));
printf("%lld\n",res);
return 0;
}
CF1620G Subsequences Galore
题目分析:
题意很抽象,稍微转化一下:\(f([t_1,t_2,\cdots,t_m])\) 代表的是 \(t_1,t_2,\cdots,t_m\) 的子序列的并集。
稍微尝试一下就会发现并集其实不好求,但是交集很好求。
因为我们的字母都是按顺序排列的,所以对于每种字母出现的次数取个 \(\min\) 然后乘起来就是交集,既然交集好球并集不好求显然可以直接容斥一下就好了。
那么最后的答案就是奇数个数的减去偶数个数的。
稍微形象一点就是这样的:
设 \(f(S)\) 表示 \(S\) 内这些字符串的子序列的交集,则:
\]
其中 \(mn_c\) 代表 \(c\) 这种字符最少的出现次数。
设 \(g(S)\) 表示 \(S\) 内这些字符串的子序列的并集,可得:
\]
可以对于奇数个和偶数个的分开处理,然后做一次高维前缀和就结束了。
但是在实现的时候需要注意,在计算 \(f(S)\) 的时候稍微精细一下,因为如果完全暴力计算的话是会被最大的一个点卡掉的。
代码:
点击查看代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#define int long long
using namespace std;
const int MOD = 998244353;
const int N = 2e4+5;
int cnt[30][30],mn[1<<23],s[2][1<<24];
char t[N];
int mod(int x){
return x >= MOD ? x - MOD : x;
}
int lowbit(int x){
return x & (-x);
}
int get(int x){
int cnt = 0;
while(x){
cnt++;
x /= 2;
}
return cnt;
}
signed main(){
int n;
scanf("%lld",&n);
for(int i=1; i<=n; i++){
scanf("%s",t+1);
int m = strlen(t+1);
for(int j=1; j<=m; j++) cnt[i][t[j] - 'a']++;
}
for(int i=0; i<26; i++){
memset(mn,0x3f,sizeof(mn));
for(int j=1; j<(1<<n); j++){
int tmp1 = __builtin_popcount(j);
mn[j] = min(mn[j ^ lowbit(j)],cnt[get(lowbit(j))][i]);
s[tmp1&1][j] = ((s[tmp1&1][j]==0) ? (mn[j]+1) : (s[tmp1&1][j] * (mn[j] + 1))%MOD);
}
}
for(int i=1; i<=n; i++){ //高维前缀和
for(int j=1; j<(1<<n); j++){
if((j >> (i-1)) & 1){
s[1][j] = mod(s[1][j] + s[1][j ^ (1<<(i-1))]);
s[0][j] = mod(s[0][j] + s[0][j ^ (1<<(i-1))]);
}
}
}
int ans = 0;
for(int i=1; i<(1<<n); i++){
int tmp1 = 0,tmp2 = 0;
for(int j=1; j<=n; j++){
if((i >> (j-1)) & 1){
tmp1++;
tmp2+=j;
}
}
ans ^= tmp1 * tmp2 * mod(s[1][i] - s[0][i] + MOD);
}
printf("%lld\n",ans);
return 0;
}
11.7
CF886E Maximum Element
题目分析:
考虑如果 \(n\) 在位置 \(i\),那么要使得返回值为 \(n\) 也就是前 \(i-1\) 个不会返回。
那么假设我们可以得到这么一个值:\(f[i]\) 代表 \([1,i]\) 的排列中间没有返回值的方案数。
那么我们最后的答案就是:
\]
其实就是枚举一下 \(n\) 的位置,前面 \(i-1\) 个只需要关注其相对大小关系所以可以看作排列,后 \(n-i\) 个随便排都可以,因为显然都一定小于 \(n\)。
那么 \(f\) 数组怎么求呢,其实也是差不多的道理:
\]
注意这个下界是 \(i-k+1\) 因为我们如果 \(i\) 的位置小于 \(i-k+1\) 那么因为后面的数一定会小于 \(i\),所以至少 \(i\) 不会不返回。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
const int MOD = 1e9+7;
int f[N],fac[N],inv[N];
int mod(int x){
return ((x % MOD) + MOD)%MOD;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
int C(int n,int m){
if(n < m) return 0;
return mod(mod(fac[n] * inv[m]) * inv[n - m]);
}
signed main(){
int n,k;
scanf("%lld%lld",&n,&k);
fac[0] = 1;
for(int i=1; i<=n; i++) fac[i] = mod(fac[i-1] * i);
inv[n] = power(fac[n],MOD-2);
for(int i=n-1; i>=0; i--) inv[i] = mod(inv[i+1] * (i + 1));
f[0] = 1;
int sum = 1;
for(int i=1; i<=n; i++){
f[i] = mod(fac[i-1] * sum);
sum = mod(sum + f[i] * inv[i]);
if(i - k >= 0) sum = mod(sum - f[i-k] * inv[i-k]);
}
int ans = fac[n];
for(int i=1; i<=n; i++){
ans = mod(ans - mod(C(n-1,i-1) * f[i-1]) * fac[n-i]);
}
printf("%lld\n",ans);
return 0;
}
CF1194F Crossword Expert
题目分析:
我们假设做出题目数为 \(i\) 的概率为 \(p[i]\) 的话,那么我们的答案就是:
\]
对于这个式子有一个经典的转化,就是设 \(P[i]\) 表示做出题目数大于等于 \(i\) 的概率,那么答案就是:
\]
那么题目数量大于等于 \(i\) 其实就是前 \(i\) 道题目使用的时间小于等于 \(T\) 就好了。
那么我们设 \(S_i\) 表示在全部不加的情况下前 \(i\) 个数所使用的时间,那么 \(P[i]\) 就是:
\]
也显然 \(T-S_i\) 大于 \(i\) 时没有意义,就直接取一个 \(\min\) 就好了。
但是这样我们依然需要 \(O(n^2)\) 去维护这个东西,不能接受。
但是我们可以发现一个事实就是:\(i\) 是均匀变化的,且 \(T-S_i\) 不升。
为了方便,我们设 \(S(n,m) = \sum_{i=0}^m \binom{n}{m}\),稍微推一下就可以发现这个式子:
&S(n,m-1) = S(n,m) - \binom{n}{m} \\
&S(n+1,m) = \sum_{i=0}^m \binom{n+1}{i} = \sum_{i=0}^m (\binom{n}{i} + \binom{n}{i-1}) = S(n,m) + S(n,m-1) = 2\times S(n,m) - \binom{n}{m}
\end{aligned}
\]
直接从小到大枚举 \(i\) 然后线性地推过去就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+7;
const int N = 5e6+5;
int fac[N],inv[N],f[N],sum[N];
int mod(int x){
return ((x % MOD)+MOD)%MOD;
}
int C(int n,int m){
if(n < m) return 0;
return mod(fac[n] * mod(inv[m] * inv[n - m]));
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
signed main(){
int n,t;
scanf("%lld%lld",&n,&t);
fac[0] = 1;
for(int i=1; i<=n; i++) fac[i] = mod(fac[i-1] * i);
inv[n] = power(fac[n],MOD-2);
for(int i=n-1; i>=0; i--) inv[i] = mod(inv[i+1] * (i + 1));
for(int i=1; i<=n; i++){
int x;scanf("%lld",&x);
sum[i] = sum[i-1] + x;
}
f[0] = 1;
int now = 0,s = 1;
for(int i=1; i<=n; i++){
if(t - sum[i] < 0) break;
int limit = min(i,t-sum[i]);
s = mod(2 * s - C(i-1,now));
while(now < limit) s = mod(s + C(i,now+1)),now++;
while(now > limit) s = mod(s - C(i,now)),now--;
f[i] = mod(s * power(power(2,i),MOD-2));
}
int ans = 0;
for(int i=0; i<=n; i++) ans = mod(ans + (f[i] - f[i+1]) * i);
printf("%lld\n",ans);
return 0;
}
11.10
[AGC002F] Leftmost Ball
题目分析:
最后我们形成的序列其实就是有 \(n\) 个白球,其他颜色的球各有 \(n-1\) 个,且满足任意一个前缀的白球数均大于等于其他颜色的种类数。
我们可以考虑设 \(f[i][j]\) 表示放了 \(i\) 个白球和 \(j\) 种其他颜色的球的方案数,转移就是去考虑从左到右第一个空位选择什么。
如果选择白球就是:
\]
因为 \(j \le i-1\) 所以一定满足 \(j \le i\) 所以就是一定合法的。
如果选择其他颜色的球就是:
\]
容易验证这样转移也一定是合法的。
解释一下这个方程:\(n - (j - 1)\) 就是剩下的没有选择的颜色里随便选一个,\(n \times k - i - (j-1) \times (k-1) - 1\) 就是我们剩下的没有放球的位置,最后减 \(1\) 是我们当前放的这一个球,\(k-2\) 就是剩下 \(k-2\) 球需要放啦。
所以总的式子就是:
\]
需要特判一下 \(k=1\) 的情况。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2005;
const int MOD = 1e9+7;
int fac[N * N],inv[N * N],f[N][N];
int mod(int x){
return x % MOD;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
int C(int n,int m){
if(n < m) return 0;
return mod(fac[n] * mod(inv[m] * inv[n-m]));
}
signed main(){
int n,k;
scanf("%lld%lld",&n,&k);
if(k == 1){
printf("1\n");
return 0;
}
fac[0] = 1;
for(int i=1; i<=n*k; i++) fac[i] = mod(fac[i-1] * i);
inv[n*k] = power(fac[n*k],MOD-2);
for(int i=n*k-1; i>=0; i--) inv[i] = mod(inv[i+1] * (i + 1));
f[0][0] = 1;
for(int i=1; i<=n; i++){
f[i][0] = 1;
for(int j=1; j<=i; j++){
f[i][j] = mod(f[i-1][j] + mod(mod(f[i][j-1] * (n - (j - 1))) * C(n * k - i - (j-1) * (k-1) - 1,k-2)));
}
}
printf("%lld\n",f[n][n]);
return 0;
}
11.12
[八省联考 2018] 林克卡特树
题目分析:
首先可以发现切掉 \(k\) 条边相当于让原图变成了 \(k+1\) 个连通块,然后再串起来求一个树的直径其实就是让我们在树上求 \(k+1\) 条不相交的链,使得他们的权值和最大。
显然可以考虑树形 \(dp\),就是设 \(dp[i][j][0/1/2]\) 代表以 \(i\) 为根的子树中有 \(j\) 条完整的链,其中 \(i\) 点的度数为 \(0/1/2\) 的最大值。
度数为 \(0\) 意味着没有相连的点,度数为 \(1\) 意味着它是链的一个端点,度数为 \(2\) 意味着有一条连接两个子树的链穿过它。
但是会发现这样状态就是 \(O(nk)\) 显然过不去,但是题目有一个提示就是我们要选择恰好 \(k\) 条边,那么就是可以考虑 \(wqs\) 二分了。
感性理解一下也可以发现,当我们以 \(k\) 为 \(x\) 轴以最优解为 \(y\) 轴,形成的图像就是一个凸的。
我们就每多选一条链多 \(mid\) 的惩罚值,二分直到最优解是 \(k\) 条链,然后跑一边将我们多加的这 \(l \times mid\) 减去就好了。
\(dp\) 的转移看代码就很好理解了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
const int INF = 1e10+5;
const double eps = 1e-5;
struct edge{
int nxt,to;
double val;
edge(){}
edge(int _nxt,int _to,double _val){
nxt = _nxt,to = _to,val = _val;
}
}e[2 * N];
struct node{
int y;
double x;
node(){}
node(double _x,int _y){
x = _x,y = _y;
}
}dp[N][4];
bool operator < (node a,node b){
if(a.x == b.x) return a.y > b.y;
return a.x < b.x;
}
node operator + (node a,node b){return {a.x + b.x,a.y + b.y};}
int cnt,head[2 * N];
double mid;
void add_edge(int from,int to,double val){
e[++cnt] = edge(head[from],to,val);
head[from] = cnt;
}
node mmx(node a,node b,node c){
return max(a,max(b,c));
}
void dfs(int now,int fath){
dp[now][0] = {0,0},dp[now][1] = {-INF,0},dp[now][2] = {mid,1}; //可以理解为一个自环啊
for(int i = head[now]; i;i = e[i].nxt){
int to = e[i].to;
if(to == fath) continue;
dfs(to,now);
dp[now][2] = mmx(dp[now][2]+dp[to][3],dp[now][1]+dp[to][0]+node(e[i].val,0),dp[now][1]+dp[to][1]+node(e[i].val-mid,-1));
dp[now][1] = mmx(dp[now][1]+dp[to][3],dp[now][0]+dp[to][0]+node(e[i].val+mid,1),dp[now][0]+dp[to][1]+node(e[i].val,0));
dp[now][0] = dp[now][0] + dp[to][3];
//一定要特别注意这个 0,1,2 的顺序,不能用 to 更新之后再去更新 to 啊
}
dp[now][3] = mmx(dp[now][0],dp[now][1],dp[now][2]);
}
int check(){
dfs(1,0);
return dp[1][3].y;
}
signed main(){
int n,k;
scanf("%lld%lld",&n,&k);++k;
for(int i=1; i<n; i++){
int from,to,val;
scanf("%lld%lld%lld",&from,&to,&val);
add_edge(from,to,val);add_edge(to,from,val);
}
double l = -INF,r = INF;
while(r - l > eps){
mid = (l + r)/2;
int tmp = check();
if(tmp == k){
l = r = mid;
break;
}
if(tmp < k) l = mid;
else r = mid;
}
mid = l;dfs(1,0);
double ans = dp[1][3].x - l * k;
printf("%.0f\n",ans);
return 0;
}
[APIO2014] 连珠线
题目分析:
可以发现我们蓝线只会有两种形态:儿子 - 自己 - 儿子 或者 儿子 - 自己 - 父亲。
而我们也可以发现对于第一种情况一定存在当某一个点当作根的时候它是儿子 - 自己 - 父亲。
所以就可以考虑先随机找一个点当根,然后换根在所有的结果中取最大值就好了。
那么 \(dp\) 就是可以设 \(dp[i][0]\) 代表以 \(i\) 为根的子树 \(i\) 不在蓝线的中点的最大值,\(dp[i][1]\) 代表以 \(i\) 为根的子树 \(i\) 在蓝线的中点的最大值。
考虑 \(dp[i][0]\) 的转移,其实还是比较简单的:
\]
其中 \(val[j]\) 代表 \((i,j)\) 这条边的边权。
考虑对于 \(dp[i][1]\) 的转移,我们可以发现对于某一个点最多是一条蓝线的中点,所以可以考虑枚举是哪一个儿子对应的蓝线的中点,而其他的儿子按 \(dp[i][0]\) 的方式转移就好了,所以也就是:
\]
那么考虑换根,如果是 \(i \to j\) 会有什么影响。
首先 \(i\) 的 \(j\) 这个儿子没了,然后 \(i\) 的父亲变成了它的儿子,\(j\) 的父亲变成了它的儿子。
所以其实可以考虑直接每一个点维护一下缺少某一个点时的这些值,然后只需要考虑父亲变成儿子造成的影响就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5+5;
const int INF = 1e18+5;
struct edge{
int nxt,to,val;
edge(){}
edge(int _nxt,int _to,int _val){
nxt = _nxt,to = _to,val = _val;
}
}e[2 * N];
int ans = -INF,cnt,head[N],len[N],fa[N],f[N][2];
vector<int> g[N][2],son[N],mx[N];
void add_edge(int from,int to,int val){
e[++cnt] = edge(head[from],to,val);
head[from] = cnt;
}
int cost(int x){
return f[x][0] + len[x] - max(f[x][0],f[x][1] + len[x]);
}
void dfs(int now,int fath){
f[now][0] = 0,f[now][1] = -INF;
int mx1=-INF,mx2=-INF;
for(int i = head[now]; i;i = e[i].nxt){
int to = e[i].to;
if(to == fath) continue;
dfs(to,now);
fa[to] = now;len[to] = e[i].val;son[now].push_back(to);
f[now][0] += max(f[to][0],f[to][1] + e[i].val);
if(cost(to) > mx1) mx2 = mx1,mx1 = cost(to);
else if(cost(to) > mx2) mx2 = cost(to);
}
f[now][1] = f[now][0] + mx1;
for(int i = head[now]; i;i = e[i].nxt){
int to = e[i].to;
if(to == fath) continue; //g 记录除去这个点之后的 dp 值,mx 记录除去这个点之后的 1 的转移
g[now][0].push_back(f[now][0] - max(f[to][0],f[to][1] + e[i].val));
if(cost(to) == mx1){
g[now][1].push_back(g[now][0].back() + mx2);
mx[now].push_back(mx2);
}
else{
g[now][1].push_back(g[now][0].back() + mx1);
mx[now].push_back(mx1);
}
}
}
void solve(int now){
for(int i=0; i < son[now].size(); i++){
int to = son[now][i];
int fath = fa[now];
f[now][0] = g[now][0][i],f[now][1] = g[now][1][i];
if(fa[now]){
f[now][0] += max(f[fath][0],f[fath][1] + len[now]);
f[now][1] = f[now][0] + max(mx[now][i],f[fath][0] + len[now] - max(f[fath][0],f[fath][1] + len[now]));
}
ans = max(ans,f[to][0] + max(f[now][0],f[now][1] + len[to]));
solve(to);
}
}
signed main(){
int n;
scanf("%lld",&n);
for(int i=1; i<n; i++){
int from,to,val;
scanf("%lld%lld%lld",&from,&to,&val);
add_edge(from,to,val);add_edge(to,from,val);
}
dfs(1,0);
solve(1);
printf("%lld\n",ans);
return 0;
}
[HNOI2012]集合选数
题目分析:
可以在题目里发现一点提示 “集合论与图论”,那么考虑是不是可以从 \(x\) 向 \(2\times x\) 和 \(3 \times x\) 建图,那么我们把这个图拉直一下,就是一个网格图,我们题目的条件就是这个网格图相邻的点不同时被选择。这个网格图大概可以理解为这个样子:
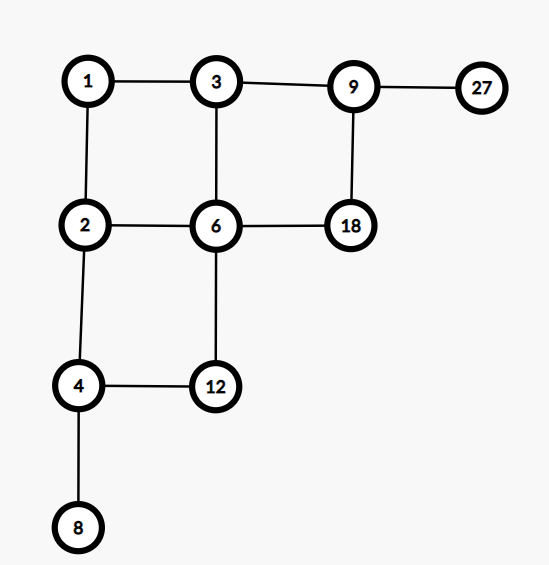
这样会发现其实不是形成一个网格图,是很多个网格图,然后就是考虑一个网格图怎么求,然后多个网格图就直接乘起来就好了。
我们可以发现形成的网格图的行数和列数都不大,一个是 \(\log_2 n\) 一个是 \(\log_3 n\),所以可以考虑直接状压,然后不能用相邻的点同时被选择就是状压的入门题了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1e9+1;
int n,a[30][30],p[30],pw[30],f[20][200005],vis[200005];
void add(int &x,int y){
x = (x + y) % MOD;
}
int dp(int x){
for(int i=1; i<=18; i++) p[i] = 0;
a[1][1] = x;
for(int i=2; i<=18; i++){ //构造矩阵
if(a[i-1][1] * 2 <= n) a[i][1] = a[i-1][1] * 2;
else a[i][1] = n+1;
}
for(int i=1; i<=18; i++){
for(int j=2; j<=11; j++){
if(a[i][j-1] * 3 <= n) a[i][j] = a[i][j-1] * 3;
else a[i][j] = n + 1;
}
}
for(int i=1; i<=18; i++){ //得到每一行的状态
for(int j=1; j<=11; j++){
if(a[i][j] <= n) p[i] += pw[j-1],vis[a[i][j]] = true;
}
}
for(int i=1; i<=18; i++){
for(int j=0; j<=p[i]; j++){
f[i][j] = 0;
}
}
f[0][0] = 1;
for(int i=0; i<=18; i++){
for(int j=0; j<=p[i]; j++){ //因为符合条件的是一个前缀,所以 p[i] 一定是 111...111,所以直接枚举
for(int k=0; k<=p[i+1]; k++){
if(!(j & k) && !(k & (k << 1))){
add(f[i+1][k],f[i][j]);
}
}
}
}
//不可能到达第 18 行,因为 2^18 > 1e5,所以就充当终止条件了。
return f[18][0];
}
signed main(){
scanf("%lld",&n);
pw[0] = 1;
for(int i=1; i<=30; i++) pw[i] = pw[i-1] * 2;
int ans = 1;
for(int i=1; i<=n; i++) if(!vis[i]) ans = (ans * dp(i))%MOD;
printf("%lld\n",ans);
}
11.15
CF28C Bath Queue
题目分析:
显然可以考虑 \(dp\)。
然后用期望推了好久都没有推出来,那么就可以考虑使用期望的定义推,也就是算方案数。
那么就可以考虑设 \(dp[i][j][k]\) 表示前 \(i\) 个洗衣房,去了 \(j\) 个人,最大值为 \(k\) 的方案数。
转移也是很显然:
\]
具体为什么要乘组合数,因为我们稍微模拟一下再手模一下会发现人和人之间是由区别的。
初值就是 \(dp[0][0][0] = 1\)
那么我们的答案就十分显然了:
\]
但是这个题仿佛会爆 \(long long\),那么用一下 \(double\) 就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 55;
double C[N][N],dp[N][N][N];
int a[N];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1; i<=m; i++) scanf("%d",&a[i]);
C[0][0] = 1;
for(int i=1; i<=n; i++){
C[i][0] = 1;
for(int j=1; j<=i; j++) C[i][j] = C[i-1][j] + C[i-1][j-1];
}
dp[0][0][0] = 1;
for(int i=0; i<m; i++){
for(int j=0; j<=n; j++){
for(int k=0; k<=n; k++){
for(int p=0; p<=n; p++){
if(j + p <= n) dp[i+1][j+p][max((p + a[i+1] - 1) / a[i+1],k)] += dp[i][j][k] * C[n-j][p];
}
}
}
}
double tmp = 0;
for(int i=1; i<=n; i++) tmp += dp[m][n][i]; //总方案数
double ans = 0;
for(int i=1; i<=n; i++) ans = ans + 1.0 * dp[m][n][i] * i / tmp;
printf("%.12f\n",ans);
return 0;
}
CF101D Castle
题目分析:
其实期望是没有什么意思的,因为我们只要可以求出最优的总的时间,除以 \(n-1\) 就是期望。
我们可以考虑设 \(dp[i]\) 表示以 \(i\) 为根的子树从 \(i\) 开始走题目要求的值是多少。
那么对于 \(dp[i]\) 它的值难道是 \(\sum_{j \in son[i]} dp[j]\) 吗?显然不是啊。
因为我们对于第 \(i\) 次访问的子树,一定会对 \(j > i\) 的子树 \(j\) 产生影响,所以只需要把影响算好就好了。
那么假设我们固定了一种转移顺序,也就是 \(v[i]\) 表示第 \(i\) 个访问的子树,那么我们的 \(dp\) 值就是:
\]
这里设 \(sz[i]\) 代表 \(i\) 这棵子树的大小,\(w[i]\) 代表 \(fa[i]\) 到 \(i\) 权值的大小,\(s[i]\) 代表完全遍历 \(i\) 这棵子树并回到 \(i\) 花费的时间。
那么就是确定转移顺序了,这个转移顺序也就是一个很显然的套路。
我们考虑对于两个儿子 \(i,j\) 若 \(i\) 在前面更优意味着什么:
首先对于 \(i,j\) 谁在前谁在后对于在 \(i,j\) 后面的数是没有影响的,只是他们两个之间的影响。
稍微推一下就可以发现其实就是:
\]
然后按照这个值排一下序按照排序后的序列直接做就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e6+5;
struct edge{
int nxt,to,val;
edge(){}
edge(int _nxt,int _to,int _val){
nxt = _nxt,to = _to,val = _val;
}
}e[2 * N];
int cnt,head[N],dp[N],s[N],sz[N],val[N];
bool cmp(int a,int b){
return (s[a] + 2 * val[a]) * sz[b] < (s[b] + 2 * val[b]) * sz[a];
}
void add_edge(int from,int to,int val){
e[++cnt] = edge(head[from],to,val);
head[from] = cnt;
}
void dfs(int now,int fath){
sz[now] = 1;//记录子树大小
s[now] = 0; //记录遍历子树需要花费的时间
vector<int> son;
for(int i = head[now]; i;i = e[i].nxt){
int to = e[i].to;
if(to == fath) continue;
dfs(to,now);son.push_back(to);
val[to] = e[i].val;
sz[now] += sz[to];s[now] = s[now] + s[to] + 2 * val[to];
}
sort(son.begin(),son.end(),cmp);
int tmp = 0;
for(int i : son) tmp += sz[i];
for(int to : son){
tmp -= sz[to];
dp[now] = dp[now] + dp[to] + sz[to] * val[to] + (s[to] + 2 * val[to]) * tmp;
}
}
signed main(){
int n;
scanf("%lld",&n);
for(int i=1; i<n; i++){
int from,to,val;
scanf("%lld%lld%lld",&from,&to,&val);
add_edge(from,to,val);add_edge(to,from,val);
}
dfs(1,0);
printf("%.8f\n",1.0 * dp[1] / (n - 1));
return 0;
}
CF1748C Zero-Sum Prefixes
题目分析:
可以发现如果我们将这些 \(0\) 正着填充完其实是不好弄的,所以就考虑倒着填充怎么做。
显然我们可以对原数组求一个前缀和变成前缀和数组,然后一次更改就变成了一段后缀的更改,而且我们可以加任意的一个数,也就是我们可以将某一个数变成任意的一个数。
那么这样来考虑对于一个 \(0\) 的位置 \(i\),我们的目的其实就是为了在不操作它的时候让他后缀的出现次数最多的数出现次数尽可能大。
其实这样的操作也就是对于两个零的位置 \(i,j\) 满足 \(i<j\) 让 \(j\) 后面的出现次数最多的数变成 \(i\) 和 \(j\) 之间出现次数最多的数。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = (int)2e5 + 8;
long long s[N];
int a[N];
int T, n;
int main() {
scanf("%d", &T);
while (T--) {
int ans = 0;
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
for (int i = 1; i <= n; i++) {
if (a[i] == 0) {
map<long long, int> _m;
_m.insert(make_pair(s[i], 1));
int max_cnt = 1;
int j = i + 1;
for (; j <= n && a[j]; j++) max_cnt = max(max_cnt, ++_m[s[j]]);
ans += max_cnt;
i = j - 1;
continue;
}
if (s[i] == 0) ans++;
}
printf("%d\n", ans);
}
return 0;
}
11.17
CF1732A Bestie
题目分析:
我们发现假设整个序列的 \(gcd\) 为 \(p\),那么我们只需要找到一个与 \(p\) 互质的位置然后操作这个位置就好了。
但是这样只是操作一次,我们也可以选择操作 \(n\) 和 \(n-1\) 两个位置,显然这样做一定可以使得 \(gcd\) 为 \(1\)。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5;
int a[N];
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%d",&t);
while(t--){
int n;
scanf("%d",&n);
int tmp = 0;
for(int i=1; i<=n; i++){
scanf("%d",&a[i]);
tmp = __gcd(tmp,a[i]);
}
if(tmp == 1){
printf("%d\n",0);
continue;
}
for(int i=n; i>=1; i--){
if(__gcd(tmp,i) == 1){
printf("%d\n",min(3,n - i + 1));
break;
}
}
}
return 0;
}
CF1732B Ugu
题目分析:
我们发现我们只需要从前到后扫一遍,发现当前位置为 \(1\) 且后面的位置存在 \(0\) 也就是这个位置必须变一下,所以就操作一次就好了。
维护是否存在 \(0\) 可以根据操作数量的奇偶来判断。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5+5;
char s[N];
bool ze[N],on[N];
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%d",&t);
while(t--){
int n;scanf("%d",&n);
scanf("%s",s+1);
for(int i=n; i>=1; i--){
ze[i] = ze[i+1] || (s[i] == '0'); //代表这个后缀是否有 1 是否有 0
on[i] = on[i+1] || (s[i] == '1');
}
int cnt = 0;
for(int i=1; i<=n; i++){
if(cnt & 1){
if(s[i] == '1') s[i] = '0';
else s[i] = '1';
}
if(s[i] == '1' && ((cnt % 2 == 1 && on[i+1]) || (cnt % 2 == 0 && ze[i+1]))) cnt++;
}
printf("%d\n",cnt);
for(int i=1; i<=n; i++){
ze[i] = on[i] = false;
}
}
return 0;
}
CF1732C2 Sheikh (Hard Version)
题目分析:
这种题一般都会考虑这样的一个性质:\(a + b \ge a \oplus b\)
因为异或本质上是不进位加法,显然不可能进位加法大。
我们显然可以考虑前缀和以及前缀异或,设 \(sum_i\) 为 \([1,i]\) 的和,\(xor_i\) 为 \([1,i]\) 的异或。
那么区间 \([l,r]\) 的价值就是 \(sum_r - sum_{l-1} - xor_r \oplus xor_{l-1}\),考虑假设我们新添加了一些数,满足这些数的和为 \(x\),异或为 \(y\),那么新区间的价值就是:
\(sum_r - sum_{l-1} + x - xor_r \oplus xor_{l-1} \oplus y\),根据上面的性质带入一下会发现,新区间的价值一定大于等于原区间的价值。
所以其实对于一个询问 \([L,R]\),最大的价值一定 \([L,R]\) 对应的区间的价值。
那么就是找到一个尽可能短的区间使得价值与 \([L,R]\) 相等了。
不进位加法与普通加法相比就是进位的不同啊,所以只要不进位就一定是合法的,我们最多只有 \(30\) 位,所以根据鸽巢原理我们能选择的数一定不超过 \(30\) 个。
所以就是直接枚举左边删多少个右边删多少个,算一下新区间的答案就好了。
但是需要注意的是我们删 \(30\) 个是指的每一个至少含有一个 \(1\) 的情况下,所以应该先把 \(0\) 全部去掉再做。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e6+5;
int sum[N],xo[N],b[N],a[N];
int calc(int l,int r){return sum[r] - sum[l-1] - (xo[r] ^ xo[l-1]);}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%lld",&t);
while(t--){
int tot = 0;
int n,q;scanf("%lld%lld",&n,&q);
for(int i=1; i<=n; i++){
scanf("%lld",&a[i]);
if(a[i] != 0) b[++tot] = i;
}
n = tot; //直接把零去掉
for(int i=1; i<=n; i++) sum[i] = sum[i-1] + a[b[i]];
for(int i=1; i<=n; i++) xo[i] = xo[i-1] ^ a[b[i]];
while(q--){
int l,r;scanf("%lld%lld",&l,&r);int tmp = l;
l = lower_bound(b+1,b+n+1,l) - b;
r = upper_bound(b+1,b+n+1,r) - b - 1;
if(l > r || n == 0){ //都是零就无所谓了
printf("%lld %lld\n",tmp,tmp);
continue;
}
int ansl = l,ansr = r;
for(int i=l; i<=min(l+30,r); i++){ //最多一边删三十个
for(int j=r; j>=max(r-30,l); j--){
if(i <= j && calc(l,r) == calc(i,j) && b[j] - b[i] < b[ansr] - b[ansl]){
ansl = i,ansr = j;
}
}
}
printf("%lld %lld\n",b[ansl],b[ansr]);
}
}
}
CF1732D2 Balance (Hard version)
题目分析:
乱搞可过,不会分析复杂度。
就是我们维护三个集合:\(S\) 代表题目中所维护的那个集合,\(S2[i]\) 代表可能成为 \(i\) 的答案的数的集合,\(S3[i]\) 代表可能有用的因数的集合。
前两个集合很好理解,第三个集合是因为当我们删除 \(i\) 的时候,\(i\) 的所有因数都会累计上 \(i\) 这个答案,所以要维护一个这个集合。
那么对于加入和删除就非常好理解了,但是注意为了复杂度我们在加入的时候并不同时将这个数在所有数的答案集合中移除,而是等。
在询问的时候我们就从小到大去看每一个可能成为答案的数,如果不在 \(S\) 中则是合法的直接输出就好了。
过程中也要维护一下 \(S3\)。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
map<int,set<int> > S2,S3;
//S2 维护可能成为答案的集合,S3 维护有用的因数集合
set<int> S; //S 维护题目中的这个集合
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int q;scanf("%lld",&q);
while(q--){
char opt;int x;
cin>>opt>>x;
if(opt == '+') S.insert(x);
else if(opt == '-'){
S.erase(x);
set<int>::iterator it = S3[x].begin();
while(it != S3[x].end()){
S2[*it].insert(x);
++it;
}
}
else{
S2[x].insert(x);
int ans = *S2[x].begin();
S3[ans].insert(x);
while(S.count(ans)){
S2[x].erase(ans);
if(S2[x].empty()) S2[x].insert(ans + x);
ans = *S2[x].begin();S3[ans].insert(x);
}
printf("%lld\n",ans);
}
}
return 0;
}
CF1740A Factorise N+M
题目分析:
可以发现一个大于 \(2\) 的偶数一定不是素数,而任何一个大于 \(2\) 的素数都一定是奇数。
所以对于不等于 \(2\) 的素数,直接用 \(3\) 拼成一个偶数,对于 \(2\) 直接用 \(2\) 拼成 \(4\) 就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;scanf("%d",&n);
if(n == 2) printf("2\n");
else printf("3\n");
}
return 0;
}
CF1740B Jumbo Extra Cheese 2
题目分析:
我们可以发现对于组成的多边形的两边的长度就等于立着的最长的边的长度,所以其实这个长度是由最长边限制的,只要最长边一定别的边无论怎么弄都是不会改变的。
我们发现这个和最长边可能有一定的关系,考虑拥有最长边的矩形,我们让最长边成为底还是成为高更优呢?
显然是成为高更优,因为成为高可以放低限制,让更小的边成为底。
那么也就是可以让任意一个矩形随便姿势摆放,都不会影响高,那么就直接让最小的当底就好了,毕竟高一定。
别忘了最后把最长边这个当高的贡献的周长加上。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int t;
scanf("%lld",&t);
while(t--){
int n;
scanf("%lld",&n);
int ans = 0,mx = 0;
for(int i=1; i<=n; i++){
int a,b;
scanf("%lld%lld",&a,&b);
mx = max(mx,max(a,b));
ans = ans + 2 * min(a,b);
}
ans = ans + 2 * mx;
printf("%lld\n",ans);
}
return 0;
}
CF1740C Bricks and Bags
题目分析:
发现绝对值显然我们是无法处理的,就考虑把绝对值化开,下面假设三个包对应的值为 \(x,y,z\) 且满足 \(x < z\)。
那么我们最终拆完的绝对值就有以下三种情况:
2\times y - x - z \\
x - z \\
x + z - 2 \times y
\end{cases}
\]
首先可以发现第二种情况显然是不优的,因为我们可以将 \(x,z\) 对应放到 \(x,y\) 这样我们就可以多一个 \(y,z\) 的贡献。
我们可以考虑枚举 \(y\) 选择什么,分类讨论:
对于第一种情况,显然除非改变 \(y\) 的选择,不然我们一定会选择比 \(y\) 小的最大的数,因为为了使得值最小。而为了尽可能地大,我们就可以直接让 \(z\) 只放一个最小的 \(a\) 这样显然就是最优的了,因为 \(y\) 无法改变,选择比他小的最大的数不会改变。
对于第三种情况类似,必选一个比他大的最小的数,剩下的放一个最大的数就好了。
可以先对数组排一遍序就可以方便很多。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e6+5;
int a[N];
signed main(){
int t;
scanf("%lld",&t);
while(t--){
int n;scanf("%lld",&n);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
sort(a+1,a+n+1);
int ans = 0;
for(int i=1; i<=n; i++){
if(i - 1 > 1) ans = max(ans,a[i] - a[i-1] + a[i] - a[1]);
if(i + 1 < n) ans = max(ans,a[i+1] - a[i] + a[n] - a[i]);
}
printf("%lld\n",ans);
}
return 0;
}
CF1740D Knowledge Cards
题目分析:
我们肯定是让最大的先到,然后次大的然后慢慢来。
所以对于其他牌来说,只要我们最大的一个还没有出现,就必须在某一个位置等着,但是一旦最大值出现就必须有办法让它走。
我们发现这里的 “有办法让它走” 其实就是等价于至少有一个位置是空的,所以我们就考虑一个个出牌,记录牌桌上最多同时会存在多少张牌。
如果牌数大于 \(n \times m - 2\) 显然就是不合法的,减二是因为 \((1,1)\) 和 \((n,m)\) 不算啊。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+5;
int n,m,k,sum[N];
int main(){
int t;
scanf("%d",&t);
while(t--){
scanf("%d%d%d",&n,&m,&k);
int mx = 0,now = k;
set<int> st;
for(int i=1; i<=k; i++){
int a;scanf("%d",&a);
st.insert(a);
while(!st.empty() && st.find(now) != st.end()){
st.erase(now);now--;
}
mx = max(mx,int(st.size()));
}
if(mx >= n * m - 3) printf("TIDAK\n");
else printf("YA\n");
}
return 0;
}
11.18
CF1740E Hanging Hearts
题目分析:
我们可以发现对于某一棵子树我们肯定至少可以获取一条最长链的长度的价值,我们就顺着来标号就好了。
而假设对于 \(i\) 点来说它的所有儿子的贡献其实是独立的,因为我们可以使得后面访问的儿子的最小值都大于前面访问的儿子的最大值。
对于 \(i\) 点我们如果选择的话就以为着我们不能选择两个以上的儿子,因为这样显然不可以构成一个不降的序列,所以选择 \(i\) 其实就可以相当于选择最长链。
所以我们可以考虑同时维护最长链和所有儿子的贡献和,然后取 \(\max\) 就是这个点的答案了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+5;
struct edge{
int nxt,to;
edge(){}
edge(int _nxt,int _to){
nxt = _nxt,to = _to;
}
}e[N];
int cnt,head[N],f[N],dp[N];
void add_edge(int from,int to){
e[++cnt] = edge(head[from],to);
head[from] = cnt;
}
void dfs(int now){
f[now] = 1;
for(int i = head[now]; i;i = e[i].nxt){
int to = e[i].to;
dfs(to);
f[now] = max(f[now],f[to] + 1);
dp[now] = dp[now] + dp[to];
}
dp[now] = max(dp[now],f[now]);
}
int main(){
int n;scanf("%d",&n);
for(int i=2; i<=n; i++){
int fa;scanf("%d",&fa);
add_edge(fa,i);
}
dfs(1);
printf("%d\n",dp[1]);
return 0;
}
11.19
\(ak\) 了一次 \(div3\) 也是有点小兴奋呢。
CF1759A Yes-Yes?
题目分析:
其实这个题需要注意的只有一点:是子串不是某个前缀。
其实也差不多,这个题也就是说 Y 后面必须是 e,e 后面必须是 s,s 后面必须是 Y,且不允许存在 Yes 之外的字符,扫一遍就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+5;
char s[N];
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;scanf("%d",&t);
while(t--){
scanf("%s",s+1);
int n = strlen(s+1);
bool flag = true;
for(int i=1; i<n; i++){
if(s[i] != 'Y' && s[i] != 's' && s[i] != 'e') flag = false;
if(s[i] == 'Y' && s[i+1] != 'e') flag = false;
if(s[i] == 'e' && s[i+1] != 's') flag = false;
if(s[i] == 's' && s[i+1] != 'Y') flag = false;
}
if(s[n] != 'Y' && s[n] != 's' && s[n] != 'e') flag = false;
if(flag) printf("Yes\n");
else printf("No\n");
}
return 0;
}
CF1759B Lost Permutation
题目分析:
既然是一个排列那么就可以直接考虑枚举是什么的排列,也就是枚举排列的最大值是多少。
这样就可以直接根据等差数列求和公式求出来这个排列的,进一步就可以得到增加的值是多少,判一下就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;scanf("%d",&t);
while(t--){
int n,s;
scanf("%d%d",&n,&s);
int mx = 0,sum = 0;
for(int i=1; i<=n; i++){
int p;scanf("%d",&p);
sum += p,mx = max(mx,p);
}
bool flag = false;
for(int i=mx; i<=200; i++){
int tmp = i * (i+1) / 2;
if(tmp - sum == s) flag = true;
}
if(flag) printf("YES\n");
else printf("NO\n");
}
return 0;
}
CF1759C Thermostat
题目分析:
大分类讨论,很恶心。
首先我们发现 \(x\) 如果变动它选择变成 \(l\) 或 \(r\) 就是最优的,所以就分别讨论一下变成 \(l\) 和变成 \(r\) 的时候是否合法然后答案求一个 \(\min\) 就好了。
需要注意 \(x=y\) 的情况。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%d",&t);
while(t--){
int l,r,x,a,b;
scanf("%d%d%d%d%d",&l,&r,&x,&a,&b);
int ans = 4;bool flag = true;
if(a == b) ans = 0;
if(abs(b - a) >= x) ans = min(ans,1);
if(abs(r - a) >= x && abs(r - b) >= x) ans = min(ans,2);
if(abs(l - a) >= x && abs(l - b) >= x) ans = min(ans,2);
if(abs(r - a) >= x && abs(l - b) >= x) ans = min(ans,3);
if(abs(l - a) >= x && abs(r - b) >= x) ans = min(ans,3);
if(abs(r - b) < x && abs(b - l) < x && a != b) flag = false;
if(ans == 4 || !flag) printf("-1\n");
else printf("%d\n",ans);
}
return 0;
}
CF1759D Make It Round
题目分析:
我们知道 \(10 = 2\times 5\),所以有多少个 \(0\) 就相当于有多少个 \(2 \times 5\) 也就是 \(2\) 和 \(5\) 的指数的 \(\min\)。
那么就考虑直接枚举有多少个 \(2 \times 5\),然后和原来就有的抵消一下,假设剩下的乘积为 \(x\),那么只要 \(x \le m\) 那么就意味着是合法的,但是因为题目要求在 \(0\) 最多的情况下最大,也就是找到 \([1,m]\) 中 \(x\) 的最大的倍数,也就是 \(\lfloor \dfrac{m}{x} \rfloor \times x\),用这个数乘以原数就是答案了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%lld",&t);
while(t--){
int n,m;scanf("%lld%lld",&n,&m);
for(int i=18; i>=0; i--){
int tmp = n;
int tw = i,fi = i;
while(tmp % 2 == 0 && tmp) tw--,tmp /= 2;
while(tmp % 5 == 0 && tmp) fi--,tmp /= 5;
int ans = 1;
while(tw > 0) ans = ans * 2,tw--;
while(fi > 0) ans = ans * 5,fi--;
if(ans <= m){
int p = m / ans * ans;
printf("%lld\n",p * n);
break;
}
}
}
return 0;
}
CF1759E The Humanoid
题目分析:
第一反应是一个贪心,也就是先用绿色再用蓝色,但是不对。
其实我们也可以发现关键就在于我们使用绿色和蓝色的顺序,而绿色和蓝色总共就只有三瓶,那么直接枚举使用的顺序然后暴力模拟一遍就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e6+5;
int a[N];
string pre[3] = {"LLB","LBL","BLL"};
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%lld",&t);
while(t--){
int n,h;scanf("%lld%lld",&n,&h);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
sort(a+1,a+n+1);
int ans = 0;
for(int opt=0; opt<3; opt++){
int w = 0,now = 1;
int g = h;
while(w <= 3){
while(a[now] < h && now <= n) h = h + a[now] / 2,now++;
if(w == 3){
ans = max(ans,now);
break;
}
if(pre[opt][w] == 'L') h = h * 2,++w;
else h = h * 3,++w;
}
h = g;
}
printf("%lld\n",ans-1);
}
return 0;
}
CF1759F All Possible Digits
题目分析:
可以发现答案一定不会超过 \(p-1\),因为我们将第一位加 \(p-1\) 次就一定可以使得每一个数都出现一次。
而这个前提下也就是意味着我们最多进一位,所以显然可以考虑分进位与不进位分类讨论。
进位的条件显然就是存在小于它的数且没有出现。
这样讨论完了之后假设第一位为 \(x\) 那么小于等于 \(x\) 的都出现过,那么我们只需要找到一个最大的且没有出现过的数让 \(x\) 加到那个数就好了。
因为我们最多有 \(100\) 个数,那么就从可能的最大值直接向下找 \(300\) 个数就一定可以找到,但是其实感觉上 \(200\) 次就够。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+5;
int a[N];
map<int,bool> vis;
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%d",&t);
while(t--){
int n,p;scanf("%d%d",&n,&p);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
for(int i=1; i<=n; i++) vis[a[i]] = true;
reverse(a+1,a+n+1);
bool flag = true;
for(int i=a[1]; i>=max(a[1]-300,0); i--){
if(!vis[i]){
flag = false;
}
}
set<int> st;
int ans = 0;
int limit = p - 1;
if(!flag){ //必须进位
ans += p - 1 - a[1] + 1;
limit = a[1] - 1;a[1] = 0;
a[2]++;
for(int i=2; i<=n; i++){
if(a[i] == p) a[i] = 0,a[i+1]++;
}
}
for(int i=1; i<=n; i++) vis[a[i]] = true;
if(a[n+1]) vis[a[n+1]] = true;
for(int i=limit; i>=max(limit-300,0); i--){
if(!vis[i]){
ans = ans + i - a[1];
break;
}
}
printf("%d\n",ans);
vis.clear();
for(int i=1; i<=n+1; i++) a[i] = 0;
}
return 0;
}
CF1759G Restore the Permutation
题目分析:
一个比较显然的想法就是从前到后,每一次选择一个最小的合法值。
这样看上去是很好,但是我们会因为选择一个最小的数而使得后面的一些数无法找到合法的值,解决也很好弄。
从后到前每一次选择一个最大的合法值,这样就不会出现这种情况,而且也显然会使得字典序最小。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+5;
int a[N];
vector<int> ans;
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%d",&t);
while(t--){
set<int> st;ans.clear();
int n;scanf("%d",&n);
for(int i=1; i<=n; i++) st.insert(i);
bool flag = true;
for(int i=1; i<=n/2; i++){
scanf("%d",&a[i]);
if(st.find(a[i]) == st.end()) flag = false;
else st.erase(a[i]);
}
if(!flag){
printf("-1\n");
continue;
}
for(int i=n/2; i>=1; i--){
set<int>::iterator it = st.lower_bound(a[i]);
if(it == st.begin()){
printf("-1\n");
flag = false;
break;
}
--it;
ans.push_back(a[i]),ans.push_back(*it);
st.erase(it);
}
if(!flag) continue;
reverse(ans.begin(),ans.end());
for(int i : ans) printf("%d ",i);
printf("\n");
}
return 0;
}
11.20
CF1750A Indirect Sort
题目分析:
我们可以观察到一点如果第一个数不是 \(1\) 那么我们无论如何都不可能让第一个数成为最小值。
而如果第一个数是 \(1\) 那么我们就可以随意地让后面交换以达到目的。
所以就是判断第一个是否为 \(1\) 就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5;
int a[N];
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
if(a[1] != 1) printf("No\n");
else printf("Yes\n");
}
return 0;
}
CF1750B Maximum Substring
题目分析:
对于 \(x \times y\) 的贡献,显然整个字符串是最优的。
对于 \(x^2\) 的贡献,显然最长的一段 \(0\) 是最优的。
对于 \(y^2\) 的贡献,显然最长的一段 \(1\) 是最优的。
那么把三个最优的值都取出来,然后取 \(\max\) 就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e6+5;
char s[N];
signed main(){
int t;
scanf("%lld",&t);
while(t--){
int n;
scanf("%lld",&n);
scanf("%s",s+1);
int ze = 0,on = 0;
for(int i=1; i<=n; i++){
if(s[i] == '0') ze++;
else on++;
}
int now = s[1] - '0',cnt = 1,res = 1;
for(int i=2; i<=n; i++){
if(s[i] - '0' != now){
now = s[i] - '0';
cnt = 1;
}
else{
cnt++;
}
res = max(res,cnt);
}
int ans = max(ze * on,res * res);
printf("%lld\n",ans);
}
return 0;
}
CF1750C Complementary XOR
题目分析:
稍微手模一下就会发现,假设我们 \(a\) 中有两个 \(1\) 分别位于 \(i,j\),那么我们操作两次:\((i,i)\) 和 \((j,j)\) 与操作一次 \((i,j)\) 的影响是一样的,显然推广到多个也是合法的。
那么我们就可以一个一个地操作 \(a\) 中的 \(1\),那么考虑什么样子的 \(b\) 是合法的。
就是 \(b\) 里面全部是 \(0\) 或者全部是 \(1\) 才是合法的。
对于全部是 \(0\) 就不用管了,对于全部是 \(1\) 直接划分为两个区间操作一下就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6+5;
char a[N],b[N];
int tag[4 * N],ze[4 * N],on[4 * N];
vector<pair<int,int> > v;
void pushdown(int now){
if(tag[now]){
tag[now<<1] ^= 1;tag[now<<1|1] ^= 1;
swap(ze[now<<1],on[now<<1]);swap(ze[now<<1|1],on[now<<1|1]);
tag[now] = 0;
}
}
void pushup(int now){
ze[now] = ze[now<<1] + ze[now<<1|1];
on[now] = on[now<<1] + on[now<<1|1];
}
void build(int now,int now_l,int now_r){
ze[now] = on[now] = 0;tag[now] = 0;
if(now_l == now_r){
if(b[now_l] == '1') on[now] = 1;
else ze[now] = 1;
return;
}
int mid = (now_l + now_r)>>1;
build(now<<1,now_l,mid);build(now<<1|1,mid+1,now_r);
pushup(now);
}
void modify(int now,int now_l,int now_r,int l,int r){
if(l <= now_l && r >= now_r){
tag[now] ^= 1;
swap(ze[now],on[now]);
return;
}
pushdown(now);
int mid = (now_l + now_r)>>1;
if(l <= mid) modify(now<<1,now_l,mid,l,r);
if(r > mid) modify(now<<1|1,mid+1,now_r,l,r);
pushup(now);
}
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%d",&t);
while(t--){
int n;scanf("%d",&n);
scanf("%s",a+1);
scanf("%s",b+1);
build(1,1,n);
for(int i=1; i<=n; i++){
if(a[i] == '1'){
if(i != 1) modify(1,1,n,1,i-1);
if(i != n) modify(1,1,n,i+1,n);
}
}
if(ze[1] == n || on[1] == n){
for(int i=1; i<=n; i++){
if(a[i] == '1'){
v.push_back({i,i});
}
}
if(on[1] == n){
v.push_back({1,n});v.push_back({1,1});v.push_back({2,n});
}
printf("YES\n");
printf("%d\n",int(v.size()));
for(auto i : v) printf("%d %d\n",i.first,i.second);
}
else printf("NO\n");
v.clear();
}
return 0;
}
CF1750D Count GCD
题目分析:
其实题目的式子可以化成这个形式:
\gcd(a[i],b[i+1]) &= a[i+1] \\
\gcd(\dfrac{a[i]}{a[i+1]},\dfrac{b[i+1]}{a[i+1]}) &= 1
\end{aligned}
\]
也就是说 \(a[i]\) 和 \(b[i+1]\) 必然是 \(a[i+1]\) 的倍数。
其实也就是找 \([1,\bigg\lfloor \dfrac{m}{a[i+1]} \bigg\rfloor]\) 中有多少个数与 \(\dfrac{a[i]}{a[i+1]}\) 互质。
这个显然可以使用容斥,也就是寻找有多少个不互质的,我们设 \(\dfrac{a[i]}{a[i+1]}\) 的唯一分解形式为 \(p_1^{k_1}\times p_2^{k_2} \times \cdots\)
其实就是求这个范围内有多少个数含有 \(p_1\) 或含有 \(p_2\) 或 \(\cdots\) 作为因数,这个就看上去应该可以就显然容斥了吧。
就是对这个数分解质因数,然后求出所有的因数,对于指数相加为奇数的取正的贡献,对于指数相加为偶数得取负得贡献就好了。
这个是某一个 \(b\) 的可能取值,那么可以直接对每一个 \(b\) 都跑一遍将方案数乘法原理求出来就好了。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e6+5;
const int MOD = 998244353;
vector<int> v;
int a[N];
int mod(int x){
return ((x % MOD) + MOD)%MOD;
}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int t;
scanf("%lld",&t);
while(t--){
int n,m;scanf("%lld%lld",&n,&m);
bool flag = true;
for(int i=1; i<=n; i++){
scanf("%lld",&a[i]);
if(i != 1 && a[i-1] % a[i] != 0) flag = false;
}
if(!flag){
printf("0\n");
continue;
}
int ans = 1;
for(int i=1; i<n; i++){
int x = m / a[i+1];
int y = a[i] / a[i+1];
//找 [1,x] 中与 y 互质的数
for(int i=2; i * i <= y; i++){
if(y % i == 0){
int p = v.size();
for(int j=0; j<p; j++) v.push_back(-v[j] * i);
v.push_back(i);
while(y % i == 0) y /= i;
}
}
if(y > 1){
int p = v.size();
for(int j=0; j<p; j++) v.push_back(-v[j] * y);
v.push_back(y);
}
int tmp = 0;
for(int i : v) tmp = mod(tmp + x / i);
ans = mod(ans * mod(x - tmp));
v.clear();
}
printf("%lld\n",ans);
}
return 0;
}
11.21
CF1761A Two Permutations
题目分析:
发现只要 \(a + b < n - 1\) 就可以构造出现,但是还有一种情况就是 \(a=b\) 且 \(a=n\) 显然也是合法的。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int t;
scanf("%d",&t);
while(t--){
int n,a,b;
scanf("%d%d%d",&n,&a,&b);
if(a + b < n - 1 || (a == b && a == n)){
printf("Yes\n");
}
else printf("No\n");
}
return 0;
}
CF1761B Elimination of a Ring
题目分析:
好恶心啊,一开始想了两个贪心都错了。
考虑如果含有不止两个数,就可以使用其中一个数去搞掉另外的数,然后这样互相搞最后一定删完,也就是答案一定是 \(n\)。
而如果只含有两个数,那么一定是形如 \(a,b,a,b,\cdots\) 的形式,会发现前 \(n-2\) 个我们没办法,只可以获得 \(\dfrac{n-2}{2}\) 的贡献,而对于最后两个我们都可以得到,所以最后的答案就是 \(\dfrac{n-2}{2} + 2\)。
需要特判 \(n=1\) 的情况。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int a[N],n;
bool vis[N];
int main(){
int t;
scanf("%d",&t);
while(t--){
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%d",&a[i]);
int cnt = 0;
for(int i=1; i<=n; i++) if(!vis[a[i]]) cnt++,vis[a[i]] = true;
if(cnt > 2) printf("%d\n",n);
else printf("%d\n",n == 1 ? 1 : (n - 2) / 2 + 2);
for(int i=1; i<=n; i++) vis[a[i]] = false;
}
return 0;
}
CF1761C Set Construction
题目分析:
考虑子集这个条件怎么弄。
我们可以考虑按照给定的子集关系建边,若 \(i\) 是 \(j\) 的子集就从 \(i\) 到 \(j\) 连边,这样跑一边拓扑序就是可以得到子集的关系。
也就是把 \(i\) 全部放到 \(j\) 里显然就可以满足子集的条件,但是不相同怎么办呢?
我们对于任意的 \(i\) 的集合中都放上一个 \(i\) 它本身,这样就可以很完美地限制好了。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e3+5;
struct edge{
int nxt,to;
edge(){}
edge(int _nxt,int _to){
nxt = _nxt,to = _to;
}
}e[N * N];
int cnt,head[N],deg[N];
char s[N][N];
set<int> st[N];
void add_edge(int from,int to){
e[++cnt] = edge(head[from],to);
head[from] = cnt;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
int n;scanf("%d",&n);
for(int i=1; i<=n; i++){
scanf("%s",s[i]+1);
}
for(int i=1; i<=n; i++) st[i].insert(i);
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(s[i][j] == '1'){
add_edge(i,j);
deg[j]++;
}
}
}
queue<int> q;
for(int i=1; i<=n; i++){
if(deg[i] == 0){
q.push(i);
}
}
while(!q.empty()){
int now = q.front();q.pop();
for(int i = head[now]; i;i = e[i].nxt){
int to = e[i].to;
for(int j : st[now]) st[to].insert(j);
deg[to]--;
if(deg[to] == 0) q.push(to);
}
}
for(int i=1; i<=n; i++){
printf("%d ",int(st[i].size()));
for(int j : st[i]) printf("%d ",j);
printf("\n");
}
for(int i=1; i<=n; i++) head[i] = 0,st[i].clear();
cnt = 0;
}
return 0;
}
CF1761D Carry Bit
题目分析:
不要管题目里给的那个式子,就是迷惑人的。
我们发现进位都是连续的一段一段的,所以其实可以分段考虑。
考虑一段进位意味着什么(我们上面一行代表 \(a\) 的二进制,下面一行代表 \(b\) 的二进制),只有可能是这种情况:
0 \cdots 1
\]
其实也就是最左端为 \((0,0)\) 最右端为 \((1,1)\),中间因为必须一直连续地进位下去所以必须至少含有一个 \(1\) 也就是以下三种情况之一:
1 \ 0 \ 1
\]
而对于不参与进位的位置来说,为了不进位,显然只可以是以下三种情况之一:
0 \ 1 \ 0
\]
然后就可以考虑枚举分了多少段,假设分了 \(p\) 段,也就是说我们要将 \(k\) 个进位分配到 \(p\) 段里每段大于等于 \(1\),经典问题。
然后将剩余的 \(n - k - p\) 个不进位的位置分配到 \(p\) 段分割成的 \(p + 1\) 个段内。\(n - k - p\) 是因为我们进位不算最前面的 \((0,0)\) 但是它也可以理解为和我们的某一段是捆绑在一起的,因为这个就是为了预防影响外界的。
然后将上面分析的三种情况乘一下,就是乘以 \(3^{k - p} \times 3^{n - k - p}\)
总结一下,设 \(calc(i,j)\) 表示将 \(i\) 个球放到 \(j\) 个盒子里,每个盒子里至少有一个的方案数,那么答案就是这个值:
\]
别急啊,这样会发现不对,少算了一些情况,少算的其实是类似这样的情况:
1 \ 1 \ 0
\]
我们会发现开头的这一段的左端点不是 \((0,0)\),因为这种情况下对于最高位而言比他还高就不可以选所以必然是 \((0,0)\) 只不过不会体现出现罢了,但是这种情况会发现也是很好算的。只需要限制第一段之前没有任何位置不进位然后多了一个不进位的位置而已,类比一下答案就是这个:
\]
两种情况显然不会重复,因为第一种相当于默认第一段最左边是 \((0,0)\),所以直接加起来就是答案。
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e6+5;
const int MOD = 1e9+7;
int fac[N],inv[N],pw[N];
int mod(int x){
return (x % MOD + MOD)%MOD;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
int C(int n,int m){
if(n < m) return 0;
return mod(fac[n] * mod(inv[m] * inv[n - m]));
}
int calc(int x,int y){
return C(x-1,y-1);
}
signed main(){
int n,k;
scanf("%lld%lld",&n,&k);
pw[0] = 1;
for(int i=1; i<=n+k; i++) pw[i] = mod(pw[i-1] * 3);
fac[0] = 1;
for(int i=1; i<=n+k; i++) fac[i] = mod(fac[i-1] * i);
inv[n+k] = power(fac[n+k],MOD-2);
if(k == 0){
printf("%lld\n",pw[n]);
return 0;
}
for(int i = n + k - 1; i>=0; i--) inv[i] = mod(inv[i+1] * (i + 1));
int ans = 0;
for(int p=1; p<=k; p++){ //枚举划分成多少段
if(n - k - p >= 0){
int tmp = mod(pw[n - k - p] * pw[k - p]); //这里相当于做的是不考虑他在最前面不要 (0,0) 的情况
int tmp2 = calc(k,p); //把 k 个小球划分到 p 个盒子里
int tmp3 = calc(n - k - p + p + 1,p + 1);
//把 n - k - p 个剩余的空位置,划分到 p + 1 个盒子里,每个盒子大于等于 0
ans = mod(ans + mod(mod(tmp * tmp2) * tmp3));
}
if(n - k - p + 1 >= 0){
//如果考虑不要 (0,0) 的话
int tmp = mod(pw[n - k - p + 1] * pw[k - p]);
int tmp2 = calc(k,p);
int tmp3 = calc(n - k - p + 1 + p,p);
ans = mod(ans + mod(mod(tmp * tmp2) * tmp3));
}
}
printf("%lld\n",ans);
return 0;
}