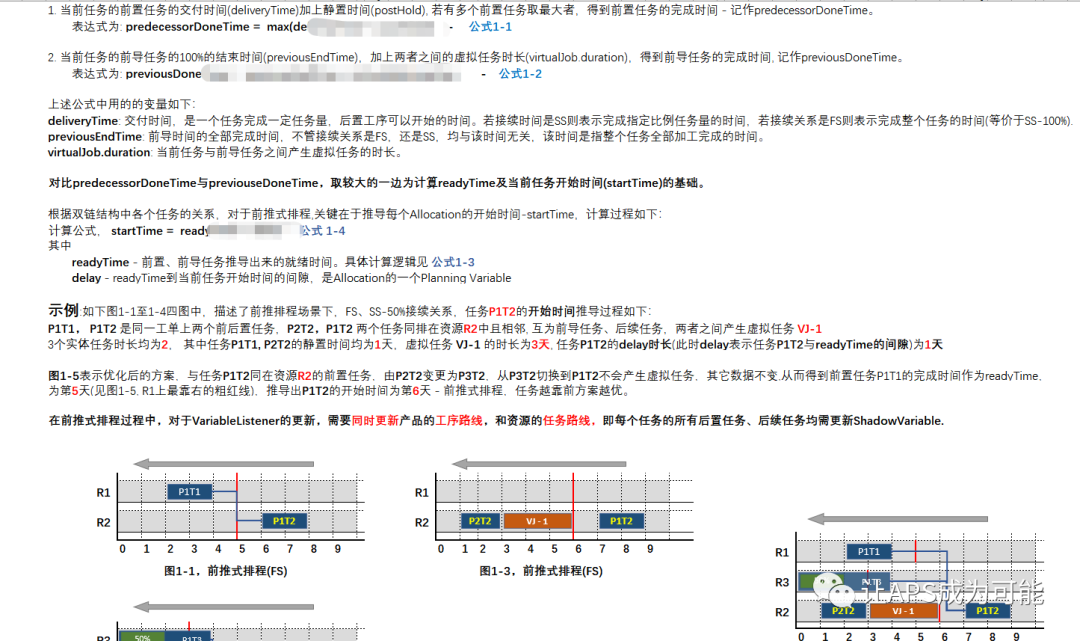
将相邻且颜色相同的点视作一个连通块，若该连通块是二分图，那么从连通块中一点\(x\)到连通块中一点\(y\)的路径的奇偶性确定

所以对于块外一点\(x\)到块内一点\(y\)，可以将它们的路径在连通块内的部分看作在一条边上反复横跳（这样奇偶性不变且当路径长度不够时可以凑长度），然后决定是否走出这条边而走向下一条边

所以在二分图中，环没有必要存在，只需要它的最小生成树即可（二分图的环的作用就是凑长度，而反复横跳一条边也可以达成这一目的，且二者都不会改变奇偶性）

若不是连通块，也就是存在奇环，那么奇偶性就会发生变化（奇环走一圈），所以奇环不能用反复横跳来替代

所以在非二分图的连通块中，我们只需要保留一个奇环即可，而为了方便，我们可以随机给一个节点连一条自环

#include<bits/stdc++.h>
#define pr pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=5e3+5,M=5e5+5,MN=1e6+5e3+5;
int n,m,Q;
char s[N];
int head[N],cnt;
struct node{
	int v,nxt;
}tree[MN];
void add(int x,int y){
	tree[++cnt].v=y,tree[cnt].nxt=head[x],head[x]=cnt;
}
vector<int> edge[N];
bool flag[N][N];
queue<pr> q;

void add1(int x,int y){
	flag[x][y]=flag[y][x]=1,q.push(pr(x,y));
}
int color[N];
bool f;
void dfs(int x,int now){
	color[x]=now;
	for(int i=0,y;i<edge[x].size();++i){
		y=edge[x][i];
		if(s[x]==s[y]){
			if(color[x]==color[y]) f=true;
			if(color[y]!=-1) continue;
			add1(x,y),add(x,y),add(y,x);
			dfs(y,now^1);
		}
	}
}
bool vis[N];
void dfs1(int x){
	vis[x]=true;
	for(int i=0,y;i<edge[x].size();++i){
		y=edge[x][i];
		if(s[x]!=s[y]&&!vis[y]) add(x,y),add(y,x),dfs1(y);
	}
}
void solve(){
	int x,y;
	while(q.size()){
		x=q.front().fi,y=q.front().se,q.pop();
		for(int i=head[x],x1;i;i=tree[i].nxt)
			for(int j=head[y],y1;j;j=tree[j].nxt){
				x1=tree[i].v,y1=tree[j].v;
				if(s[x1]==s[y1]&&!flag[x1][y1]) add1(x1,y1);
			}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&Q);
	getchar(); cin>>s+1;
	for(int i=1,u,v;i<=m;++i) scanf("%d%d",&u,&v),edge[u].push_back(v),edge[v].push_back(u);
	for(int i=1;i<=n;++i) add1(i,i),color[i]=-1; 
	for(int i=1;i<=n;++i){
		f=false;
		if(color[i]!=-1) continue;
		dfs(i,1);
		if(f) add(i,i);
	}
	for(int i=1;i<=n;++i) if(!vis[i]) dfs1(i);
	solve();
	while(Q--){
		int u,v; scanf("%d%d",&u,&v);
		printf(flag[u][v]?"YES\n":"NO\n");
	}
	return 0;
}