一、定义
在一棵无根树中,若需要分别计算以多个节点为根的多个答案,而当节点总数 \(n\) 过大时,则可以考虑使用 二次扫描与换根法 。
二、解法
解决方法如下:换根 dp 通常会与树形 dp 结合,我们可以先任定一个根节点 \(root\) ,通过树形 dp 的思想计算出一个答案,再考虑当 \(root\) 的子节点作为根节点时,答案怎样变化。一般可以在 \(O(1)\) 的复杂度内完成答案的转化。这样整道题的复杂度就由 \(O(n ^ 2)\) 降为了 \(O(n)\)
在代码中,我们一共需要两个 \(dfs\) 函数,第一个处理以 \(root\) 为根时的答案,第二个进行换根操作。具体见例题。
三、例题
1、Sta
分析:
此题非常经典和模板。我们可以先求解出以节点 1 为根节点时的答案,再考虑换根。
见下图:
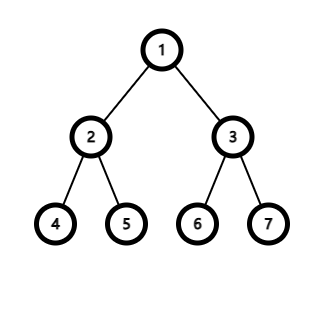
显然,当 1 的儿子节点 3 成为根时,3 和 3 的子树中的所有节点的深度都会减 1,而其它节点的深度都会加 1。推广一下即得:设以 \(i\) 为根时的答案为 \(dp_i\) ,其子树(包括自己)的节点一共有 \(size_i\) 个 ,若有两个节点 \(u\) 和 \(v\),\(v\) 是 \(u\) 的儿子节点,则有: \(dp_v = dp_u - size_v + (n - size_v)\) ,这样我们就以 \(O(1)\) 的时间复杂度得到了以另一个节点为根时的答案。
Code:
#include<bits/stdc++.h>
using namespace std;
#define SF scanf
#define PF printf
#define int long long
struct Edge {
int to, next;
}edge[2000005];
int head[1000005], cnt, dep[1000005], siz[1000005], dp[1000005], n;
void add(int u, int v) {
edge[++cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt;
}
void dfs1(int x, int fa) {
dep[x] = dep[fa] + 1;
siz[x] = 1;
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
dfs1(to, x);
siz[x] += siz[to];
}
}
void dfs2(int x, int fa) {
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
dp[to] = dp[x] - siz[to] + (n - siz[to]);
dfs2(to, x);
}
}
signed main() {
SF("%lld", &n);
for(int i = 1; i < n; i++) {
int u, v;
SF("%lld%lld", &u, &v);
add(u, v), add(v, u);
}
dfs1(1, 0);
for(int i = 1; i <= n; i++) dp[1] += dep[i];
dfs2(1, 0);
int ans = 0, index;
for(int i = 1; i <= n; i++) {
if(dp[i] > ans) ans = dp[i], index = i;
}
PF("%lld", index);
return 0;
}
2、积蓄程度
分析:
我们先考虑一个节点最多能蓄的水受哪些因素影响。
首先,若它的所有儿子最多只能蓄 \(a\) 的水,那它蓄的水一定不能超过 \(a\) ,不然无法满足儿子的条件。其次,如果它的父亲到它间的河道只能蓄 \(b\) 的水,那它最多只能得到 \(b\) 的水。所以,它最多能蓄的水就是 \(\min(a, b)\) 。不过为了换根方便,我们可以把 \(a\) 和 \(\min(a, b)\) 都存下来。
现在思考如何换根。
令 \(dp_i\) 为以 \(i\) 为根时的答案, \(sum_i\) 为 \(i\) 节点的所有儿子最多蓄的水。若有两个节点 \(u\) 和 \(v\) , \(v\) 是 \(u\) 的儿子节点,他们之间的河道能蓄 \(w\) 的水。因为现在 \(u\) 是根节点,自身能得到无限多的水,易证 \(dp_u = sum_u\), 换根后显然 \(v\) 就变成了 \(u\) 的父亲节点。此时 \(u\) 的儿子最多能蓄的水就变成了 \(dp_u - sum_v\),而 \(u\) 节点最多也只能得到 \(w\) 的水了。因此 \(u\) 对 \(v\) 的贡献即为 \(\min(dp_u - sum_v, w)\),再加上 \(v\) 原来儿子能蓄的水,即得到了 \(dp_v\) 。
方程式可写作: \(dp_v = sum_v + \min(dp_u - sum_v, w)\)。
但有一种特殊情况:如果 \(u\) 节点只能到达 \(v\) 这一个节点,那么换根后 \(u\) 节点一定是叶子节点,可以排无限多的水。贡献即为它最多能得到的水 \(w\) 。 写作: \(dp_v = sum_v + w\)
Code:
#include<bits/stdc++.h>
using namespace std;
#define SF scanf
#define PF printf
#define int long long
struct Edge {
int to, next, w;
}edge[400005];
int head[200005], cnt, dp[2][200005], n, ans[200005], d[200005];
// 0 儿子最多能装的 1 自己最多能装的
void add(int u, int v, int w) {
edge[++cnt].to = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
}
void dfs1(int x, int fa, int Max) {
bool flag = true;
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
flag = false;
dfs1(to, x, edge[i].w);
dp[0][x] += dp[1][to];
}
dp[1][x] = min(Max, dp[0][x]);
if(flag) dp[1][x] = Max;
}
void dfs2(int x, int fa) {
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
if(d[x] == 1) ans[to] = dp[0][to] + edge[i].w;
else ans[to] = dp[0][to] + min(ans[x] - dp[1][to], edge[i].w);
dfs2(to, x);
}
}
signed main() {
int t;
SF("%lld", &t);
while(t--) {
cnt = 0;
memset(head, 0, sizeof(head));
memset(dp, 0, sizeof(dp));
SF("%lld", &n);
for(int i = 1; i < n; i++) {
int u, v, w;
SF("%lld%lld%lld", &u, &v, &w);
d[u]++, d[v]++;
add(u, v, w), add(v, u, w);
}
dfs1(1, 0, 1e18);
ans[1] = dp[1][1];
dfs2(1, 0);
int sum = 0;
for(int i = 1; i <= n; i++) sum = max(sum, ans[i]);
PF("%lld\n", sum);
}
return 0;
}
3、概率充电器
分析:
首先我们要知道期望是什么。
现有 \(n\) 个事件,我们对第 \(i\) 个事件有一个期望值 \(a_i\) ,且第 \(i\) 个事件发生的概率为 \(b_i\) ,则总的期望值即为:\(\sum_{i=1}^{n}{a_ib_i}\)
在此题中,我们对每个元件进入充电状态的期望固定为 1 ,因此我们只需要计算所有元件进入充电状态的概率的总和就行了。
其次,我们要了解最基本的有关于概率的知识。
假设现有两个事件 \(A\) 和 \(B\) , \(A\) 发生的概率为 \(a\) , \(B\) 发生的概率为 \(b\) 。那么请问 \(A\) 和 \(B\) 中至少发生一个事件的概率为多少呢?
结论:概率为 \(a + b - ab\) 。证明如下:
\(A\) 发生且 \(B\) 不发生的概率为: \(a * (1 - b) = a - ab\)
\(A\) 不发生且 \(B\) 发生的概率为: \(b * (1 - a) = b - ab\)
\(A\) 和 \(B\) 都发生的概率为: \(ab\)
将它们相加即可。
现在回到题目里。一个元件的电有三个来源:来自父亲,来自自己,来自儿子。后两个较好解决。设第 \(i\) 个元件充上电的概率为 \(dp_i\) ,则对于第 \(u\) 个元件,自己直接充电的概率为 \(q_u\) ,儿子 \(v\) 给自己充电的概率为 \(dp_v * w\) , \(w\) 即为它们间通电的概率。显然现在有两个事件,套用上述公式即可。
具体即为: \(dp_u = q_u + dp_v * w - q_u * dp_v * w\),求出所有节点对应的 \(dp_i\) 可以在第一次扫描里解决。
现在考虑第一种情况:来自父亲。
若父亲 \(u\) 向儿子 \(v\) 通电的概率为 \(w\) ,则 \(u\) 的电的来源分为两种情况讨论:是 \(v\) 转移过来的,不是 \(v\) 转移过来的。设它们分别为事件 \(C\) 和事件 \(D\) ,发生的概率分别为 \(c\) 和 \(d\) 。不难发现 \(c = dp_v * w\) 。所以我们只需要求出 \(d\) 即可。
根据换根 dp 的性质,我们已经得到了 \(dp_u\) 的最终答案。因此有: \(c + d - c * d = dp_u\) ,将 \(c\) 带入求解 \(d\) 就可以了。需要注意的是: \(d\) 最终化简出来会是一个分数,你需要判断是否有解。
得到这些之后,转移出 \(dp_v\) 已经不难了。两种可能:由父亲转移过来,即 \(d * w\) (为什么不是 \(dp_u * w\) ?因为既然是父亲影响儿子,那儿子一定不可能对父亲造成影响),不由父亲转移过来,即第一次得到的 \(dp_v\) 。
所以套用公式,即可得到: \(dp_v = dp_v + d * w - dp_v * d * w\) 。
Code:
#include<bits/stdc++.h>
using namespace std;
#define SF scanf
#define PF printf
struct Edge {
int to, next;
double w;
}edge[1000005];
int head[500005], cnt;
double dp[500005];
const double eps = 1e-8;
void add(int u, int v, double w) {
edge[++cnt].to = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
}
void dfs1(int x, int fa) {
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
dfs1(to, x);
dp[x] = dp[x] + dp[to] * edge[i].w - dp[x] * dp[to] * edge[i].w;
}
}
void dfs2(int x, int fa) {
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
if(fabs(dp[to] * edge[i].w - (double)(1.0)) <= eps) dfs2(to, x); //判分母是否为0
else {
double a = (dp[x] - dp[to] * edge[i].w) / (1 - dp[to] * edge[i].w);
dp[to] = dp[to] + a * edge[i].w - dp[to] * a * edge[i].w;
dfs2(to, x);
}
}
}
int main() {
int n;
SF("%d", &n);
for(int i = 1; i < n; i++) {
int u, v;
double w;
SF("%d%d%lf", &u, &v, &w);
add(u, v, w / 100.0), add(v, u, w / 100.0);
}
for(int i = 1; i <= n; i++) SF("%lf", &dp[i]), dp[i] /= 100.0;
dfs1(1, -1);
dfs2(1, -1);
double ans = 0;
for(int i = 1; i <= n; i++) ans += dp[i];
PF("%.6lf", ans);
return 0;
}
4、计算机
分析:
设节点 \(i\) 到其它节点的最远距离为 \(dp_i\) ,那么距离 \(i\) 最远的节点有两种可能:在 \(i\) 的子树里,或是 \(i\) 的祖先。第一种情况很好考虑。求出它的儿子 \(v\) 对应的 \(dp_v\) ,如果 \(i\) 到 \(v\) 的距离是 \(w\) ,那么 \(v\) 对于 \(i\) 的贡献即为: \(dp_v + w\),所以可得: \(dp_i = \max\{dp_v + w\}\)
在换根 dfs 中考虑第二种情况。
若父亲 \(u\) 和儿子 \(v\) 间的距离为 \(w\) ,那么父亲 \(u\) 对其的贡献即为 \(w + dp_u\) 。
什么,你想 Hack 我?
确实很好 Hack ,请看下图:
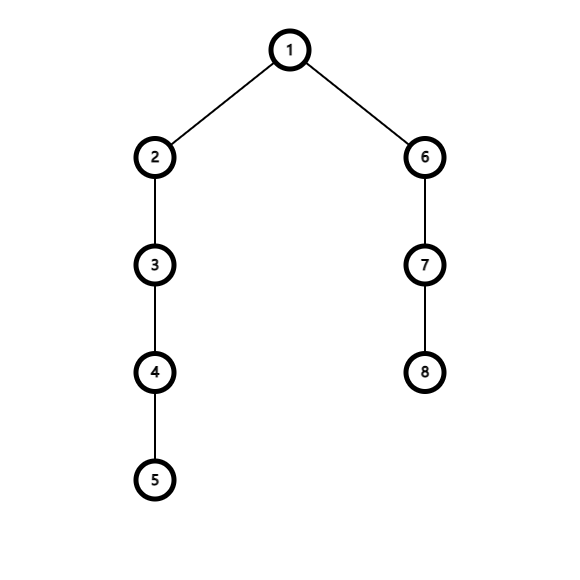
令此图中所有的边权都为 1 ,显然 \(dp_1 = 4\) ,但如果想要转移出 \(dp_2\) ,按照上述思路得到的答案是 5 ,但真实答案应该为 4 ,这是因为节点 \(u\) 的答案路径中包括了 \(v\) 。那么如何解决呢?
我们设节点 \(i\) 到其它节点的次远距离为 \(cmax_i\) ,且设其答案路径中的第一个儿子节点为 \(pos_i\) ,则如果当前需要转移的节点 \(v\) 就是 \(pos_u\) ,则 \(u\) 对其的贡献就变成了 \(\max\{dp_u - w, cmax_u + w\}\) ,否则就像上述一样转化。至此,本题主要思路完结。
当然,在进行换根 dp 的同时需要实时更新 \(dp\) , \(cmax\) 以及 \(pos\) 的值。因为第一次 dfs 得到的值只是在其子树中的最优,加入父亲的贡献后最优可能会发生变化。
Code:
#include<bits/stdc++.h>
using namespace std;
#define SF scanf
#define PF printf
struct Edge {
int to, next, w;
}edge[20005];
int head[10005], cnt, Max[2][10005], dp[10005], p[10005];
// 0 最大 1 次大
void add(int u, int v, int w) {
edge[++cnt].to = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
}
void dfs1(int x, int fa) {
Max[0][x] = 0, Max[1][x] = 0x3f3f3f3f;
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
dfs1(to, x);
int now = Max[0][to] + edge[i].w;
if(now > Max[0][x]) Max[1][x] = Max[0][x], Max[0][x] = now, p[x] = to;
else if(now > Max[1][x]) Max[1][x] = now;
}
}
void dfs2(int x, int fa) {
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
if(to == p[x]) {
Max[0][to] = max(dp[x] - edge[i].w, edge[i].w + Max[1][x]);
Max[1][to] = max(Max[1][to], min(dp[x] - edge[i].w, edge[i].w + Max[1][x]));
if(edge[i].w + Max[1][x] == Max[0][to]) p[to] = x;
else p[to] = p[p[x]];
dp[to] = Max[0][to];
}
else {
Max[0][to] = dp[to] = dp[x] + edge[i].w;
p[to] = x;
}
dfs2(to, x);
}
}
int main() {
int n;
while(SF("%d", &n) != EOF) {
memset(Max, 0, sizeof(Max));
memset(dp, 0, sizeof(dp));
memset(head, 0, sizeof(head));
cnt = 0;
for(int i = 2; i <= n; i++) {
int u, w;
SF("%d%d", &u, &w);
add(i, u, w), add(u, i, w);
}
dfs1(1, -1);
dp[1] = Max[0][1];
dfs2(1, -1);
for(int i = 1; i <= n; i++) PF("%d\n", dp[i]);
}
return 0;
}
5、连珠线
本人觉得最有意思同时也是最难的一道题目
提醒:该题目会用到上一题的思想,建议弄懂上一题后再进行阅读。
拿到题之后很可能会看不懂。没关系,我们要学会转化题意。
给出一棵树,一些边是蓝色的,剩下的边都是红色的。蓝色的边权值总和作为答案,求答案可能的最大值。
当然蓝色的边是有限制条件的。不然还需要你来做?,见下图,当树的结构形如。
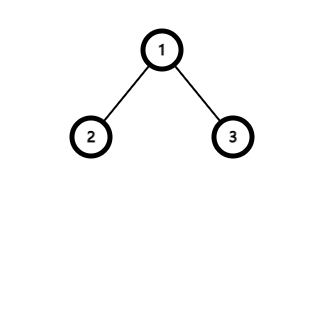
或者
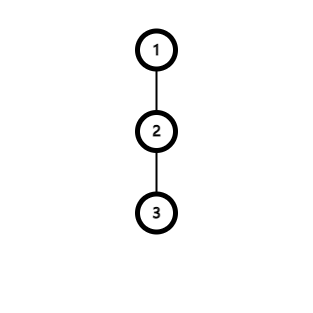
时,其边可以为蓝色。
其实我们把第一棵树拉直后,结构也就变成了第二棵树。
问题来了,怎么求呢?
我们设 \(dp_{0, i}\) 为以 \(i\) 为根节点,且 \(i\) 不是蓝色边中点时的答案。设 \(dp_{1, i}\) 为以 \(i\) 为根节点,且 \(i\) 是蓝色边中点时的答案。
第一种情况稍微好处理一点。设当前节点 \(u\) 和其儿子节点 \(v\) 间的边权为 \(w\) ,则若 \(u\) 不是中点,那 \(v\) 要么是中点(此时它们间的边为蓝色边),要么不是中点(此时它们间的边为红色边)。这两个贡献取较大的即为 \(v\) 对 \(u\) 的贡献。即:\(dp_{0, u} = dp_{0, u} + \max\{dp_{1, v} + w, dp_{0, v}\}\) 。
接下来考虑第二种情况:
如果 \(u\) 是中点,那么根据上面的两幅图可知,它只能与它的一个儿子节点 \(v\) 构成中点和非中点的关系,贡献即为: \(dp_{0, v} + w\) 。其余所有儿子节点都只能按照 \(u\) 不是中点的情况转移。所以方程式可写为: \(dp_{1, u} = dp_{0, u} + \max\{dp_{0, v} + w\}\) 。
但是好像有什么问题?
显然,选出来的最优节点 \(v\) 对于 \(dp_{0, u}\) 的贡献不应该累计在 \(dp_{1, u}\) 里。所以应该减去之前推出的贡献 \(\max\{dp_{1, v} + w, dp_{0, v}\}\) 。
因此最终的转移方程式可记作: \(dp_{1, u} = dp_{0, u} + \max\{dp_{0, v} + w - \max\{dp_{1, v} + w, dp_{0, v}\}\}\) 。
然后考虑如何换根。
为了避免混淆之前得到的答案,我们令 \(now\) 数组为换根时的意义与 \(dp\) 数组相同的新数组, \(ans_i\) 为以 \(i\) 为根节点时的答案。
设当前节点 \(u\) 和它的儿子节点 \(v\) 间有一条权值为 \(w\) 的边。则当 \(v\) 变成根的时候,原先对 \(u\) 的贡献就没有了。即为: \(now_{0, u} = ans_u - \max\{dp_{1, v} + w, dp_{0, v}\}\) 。
那么 \(now_{1, u}\) 怎么转化呢?
类比上面的做法,我们在第一次 dfs 的时候用一个数组 \(maxn\) 来记录当 \(u\) 为根节点时,最大的 \(dp_{0, v} + w - \max\{dp_{1, v} + w, dp_{0, v}\}\) 。所以 \(now_{1, u} = now_{0, u} + maxn_u\) 。
但是这真的正确吗?
和上一题的思想一样,如果 \(v\) 就在 \(maxn_u\) 的路径上,那我们也应该用次大值来更新。设其为 \(cmaxn\) 。
所以也需要一个 \(pos\) 数组来存 \(maxn_u\) 路径上的第一个节点,如果当前节点 \(v = pos_u\) ,则方程就应写作: \(now_{1, u} = now_{0, u} + cmaxn_u\)
当然,这并不是最终的 \(now_{1, u}\) 。因为在换根后,原来 \(u\) 的父亲节点 \(fa\) 也会变成 \(u\) 的儿子节点,对 \(now_{1, u}\) 可能有贡献。设 \(fa\) 到 \(u\) 间的边的边权为 \(S\) ,所以类比上面的思路可得: \(now_{1, u} = \max(now_{1, u}, now_{0, u} + now_{0, fa} + S - \max(now_{1, fa} + S, now_{0, fa}))\) 。这样才算拿到了最后的 \(now_{1, u}\) 。
那么为什么不用考虑 \(fa\) 对 \(now_{0, u}\) 的贡献呢?
因为我们在计算的时候已经得到了最终答案 \(ans_u\) ,而根节点一定是作为蓝线的中心节点的,即: \(ans_u = dp_{0, u}\) 。换句话说, \(fa\) 对 \(now_{0, u}\) 的贡献早就计算进去了。对 \(now_{0, u}\) 进行修改只是为了换根的时候好处理一点。
虽然但是,在计算 \(ans_v\) 的时候,真的可以直接写成 \(ans_v = dp_{0, v}\) 吗?
当然不行!
还得把父亲 \(u\) 对其的贡献加进去。
由于根节点一定是作为蓝线的中心节点的,所以可写作: \(ans_v = dp_{0, v} + \max\{now_{0, u}, now_{1, u} + w\}\) 。
至此,本题完美结束。可以看一下代码,也许会思路更清晰一点。
Code:
#include<bits/stdc++.h>
using namespace std;
#define SF scanf
#define PF printf
struct Edge {
int to, next, w;
}edge[400005];
int head[200005], cnt, dp[2][200005], now[2][2000005], Max[2][200005], sum[200005], p[200005];
// 0 不是中点 1 是中点
// 0 最大 1 次大
void add(int u, int v, int w) {
edge[++cnt].to = v;
edge[cnt].next = head[u];
edge[cnt].w = w;
head[u] = cnt;
}
void dfs1(int x, int fa) {
Max[0][x] = Max[1][x] = -0x3f3f3f3f;
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
dfs1(to, x);
dp[0][x] += max(dp[1][to] + edge[i].w, dp[0][to]);
int now = dp[0][to] + edge[i].w - max(dp[1][to] + edge[i].w, dp[0][to]);
if(now > Max[0][x]) Max[1][x] = Max[0][x], Max[0][x] = now, p[x] = to;
else if(now > Max[1][x]) Max[1][x] = now;
}
dp[1][x] = dp[0][x] + Max[0][x];
}
void dfs2(int x, int fa, int w) {
for(int i = head[x]; i; i = edge[i].next) {
int to = edge[i].to;
if(to == fa) continue;
int k = Max[0][x];
if(p[x] == to) k = Max[1][x];
now[0][x] = sum[x] - max(dp[1][to] + edge[i].w, dp[0][to]);
now[1][x] = now[0][x] + k;
if(fa != -1) now[1][x] = max(now[1][x], now[0][x] + now[0][fa] + w - max(now[1][fa] + w, now[0][fa]));
sum[to] = dp[0][to] + max(now[0][x], now[1][x] + edge[i].w);
dfs2(to, x, edge[i].w);
}
}
int main() {
int n, ans = 0;
SF("%d", &n);
for(int i = 1; i < n; i++) {
int u, v, w;
SF("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, w);
}
dfs1(1, -1);
sum[1] = dp[0][1];
dfs2(1, -1, 114514);
for(int i = 1; i <= n; i++) ans = max(ans, sum[i]);
PF("%d", ans);
return 0;
}