深入分析：矩阵梯度类实例研究

写在前面

本文主要用于围绕矩阵类求梯度等问题进行证明与分析，由于笔者的数理基础浅薄，下面的证明过程若存在错误，欢迎评论指正。

分子布局和分母布局是什么？

分子布局表示求导的结果维度以分子为主，如向量$y$关于标量$x$求导，结果的维度和y的维度是一致的，如果$y$为列向量，那么结果为列向量。
分母布局表示求到的结果维度以分母为主，如向量$y$关于标量$x$求导，$y$为行向量，那么结果为列向量；如标量$y$对矩阵$X$求导，按分母布局则求导结果的维度和$X$一致为$m\times n$，安分子布局则求导结果的维度为$n\times m$。分子布局和分母布局之间相差一个转置。

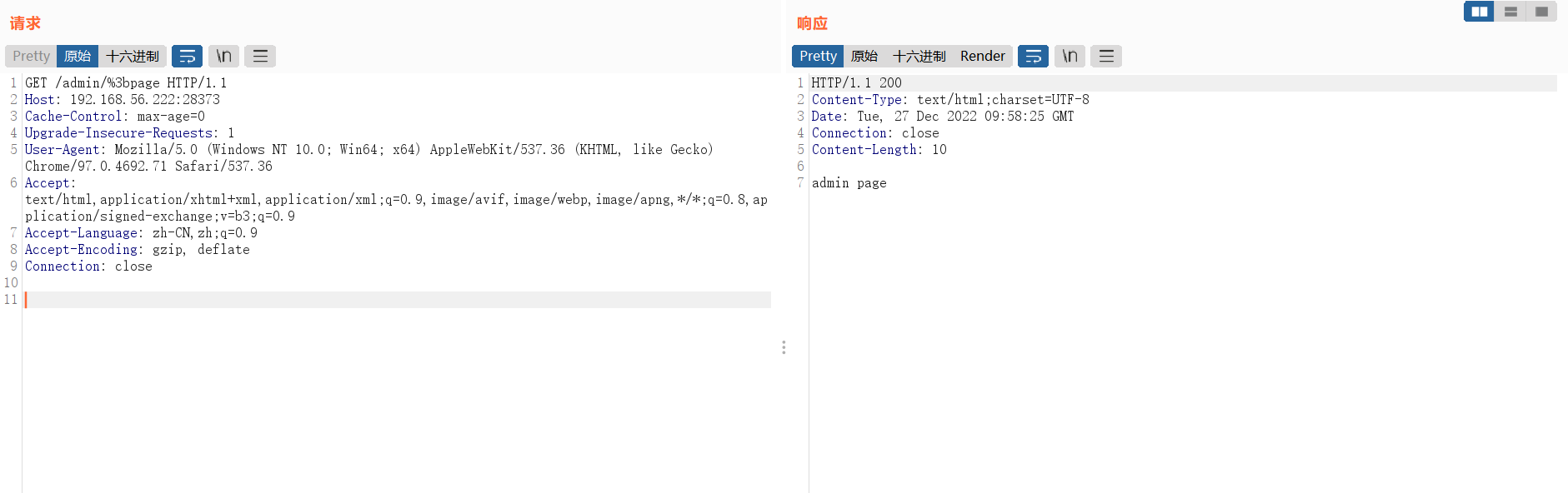
上述问题适合于标量对向量或矩阵，向量或矩阵对标量求导等情况。在向量对向量求导中，以列向量对列向量求导为例，$m$维列向量$y$对$n$维列向量$x$求导，其可以表示为$mn$个标量对标量的求导，求导结果一般排列为一个矩阵。如果为分子布局，矩阵的第一个维度以分子为准，结果是$m\times n$矩阵；如果为分母布局，矩阵的第一个维度以分母为准，分别如下所示：

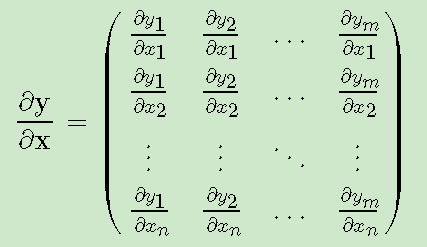
按分子布局的向量对向量求导的结果矩阵，我们一般叫做雅克比 (Jacobian)矩阵。
按分母布局的向量对向量求导的结果矩阵，我们一般叫做梯度矩阵。

矩阵微分和梯度的关系是什么？

矩阵梯度的通用方法：先将矩阵写成微分形式，$df=tr(GdX)$，然后得到$\nabla f=G^T $
矩阵微分求解得到的算子可称为偏导算子，梯度矩阵通常是偏导算子的转置。

案例1

$\begin{array}{ll}\min_{U}&\dfrac{1}{2}\left\|\boldsymbol{R}\circ\left(\boldsymbol{Y}-\boldsymbol{UV}^{\top}\right)\right\|_{F}^{2}+\dfrac{\lambda_{1}}{2}\left\|\boldsymbol{U}-\boldsymbol{SU}\right\|_{F}^{2}+\dfrac{\lambda_{3}}{2}\left\|\boldsymbol{U}-\boldsymbol{T}\right\|_{F}^{2}.\end{array}$

在上式中，主要目的为更新$U$，其中$V,Z,W,b$固定,$T=\psi(X)W+1b^T=KA+1b^T$

首先对第一项求导，可以得到以下过程：

$\underset{U}{\text{min}}\dfrac{1}{2}\left\|R\circ\left(Y-UV^{\mathrm{T}}\right)\right\|_{F}^{2}\Rightarrow\nabla U=R\circ\left(UV^{\mathrm{T}}-Y\right)V$

1、将第一项展开可以得到如下形式：

$\frac{1}{2}tr\{R^T\circ(Y-UV^T)^T(R\circ(Y-UC^T)) \}=\frac{1}{2} tr\{ R^T\circ(Y^T-VU^T)(R\circ(Y-UV^T))\}=\frac{1}{2}tr\{R^T\circ Y^T \cdot R \circ Y-2R^T\circ VU^T \cdot R\circ Y+\\ R^T\circ VU^T\cdot R \circ Y+R^T\circ VU^T\cdot R \circ UV^T \}$

2、上式中第一项为与$U$无关项，可以忽略，下面对后面2项分别求导即可：

2.1 下面使用了$tr(AB)=tr(BA)$的性质

$\frac{1}{2}\mathrm{tr}\left(-2(R\circ Y)\cdot\left(R^{\mathrm{T}}\circ V d(U^{\mathrm{T}})\right)\right) +\frac{1}{2}\left[\mathrm{tr}\left(\left(R\circ U V^{\mathrm{T}}\right)\cdot R^{\mathrm{T}}\circ V d(U^{\mathrm{T}})+\right.\right.\operatorname{tr}\left(\left(R^\mathrm{T}\circ VU^\mathrm{T}\circ R^\mathrm{T}\right)\cdot d(U)V^\mathrm{T}\right]$

2.2 下面使用了$tr(A(B\circ C))=tr((A\circ B^T)C)$的性质

$\frac{1}{2}\mathrm{tr}\left(-2((R\circ Y)\circ R)\cdot\left(V d(U^{\mathrm{T}})\right)\right)+\frac{1}{2}\left[\mathrm{tr}\left(\left(\left(R\circ U V^{\mathrm{T}}\right)\circ R\right)\cdot V d(U^{\mathrm{T}})\right)+\mathrm{tr}\left(\left(R^{\mathrm{T}}\circ V U^{\mathrm{T}}\right)\cdot d(U)V^{\mathrm{T}}\right)\right]$

2.3 下面这项规定不一定通用，原文给出的$R$为指示矩阵,$\{r_{ij}\}=1$,$1$和$1$的哈达玛内积必然为$1$，因此有$R\circ R=R$

$\frac{1}{2}\mathrm{tr}(-2)(R\circ V)\cdot V d\left(U^{T}\right)+\frac{1}{2}\left[\mathrm{tr}\left(\left(R\circ U V^{T}\right)\cdot V d\left(U^{T}\right)\right)+\mathrm{tr}(V^{T}\left(R^{T}\circ V U^{T}\right)\cdot d(U))\right]$

2.4 将最后一项利用$tr(A)=tr(A^T)$性质,那么2.3中式子可以更新为:

$\begin{array}{r l}{-}&{\left(R\circ Y\right)\cdot V+\frac{1}{2}\times\left[\left(R\circ U V^{\mathrm{T}}\right)\cdot V+\left(R\circ U V^{\mathrm{T}}\right)\cdot V\right]}\end{array}$

2.5 进一步简化可以得到其关于$U$的偏导为$R\circ\left(UV^\mathrm{T}-Y\right)V\text{}$