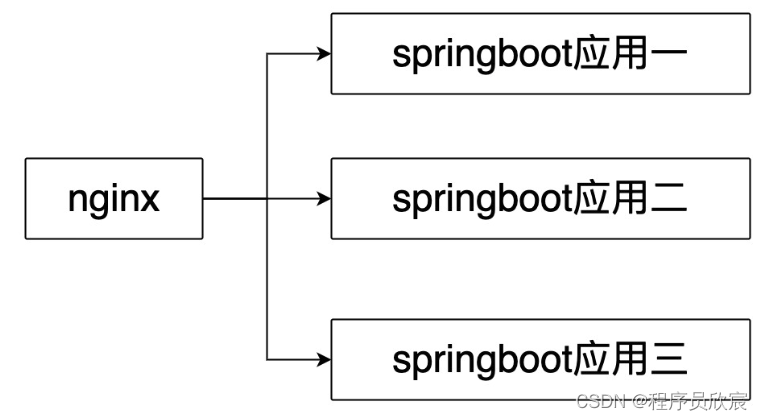
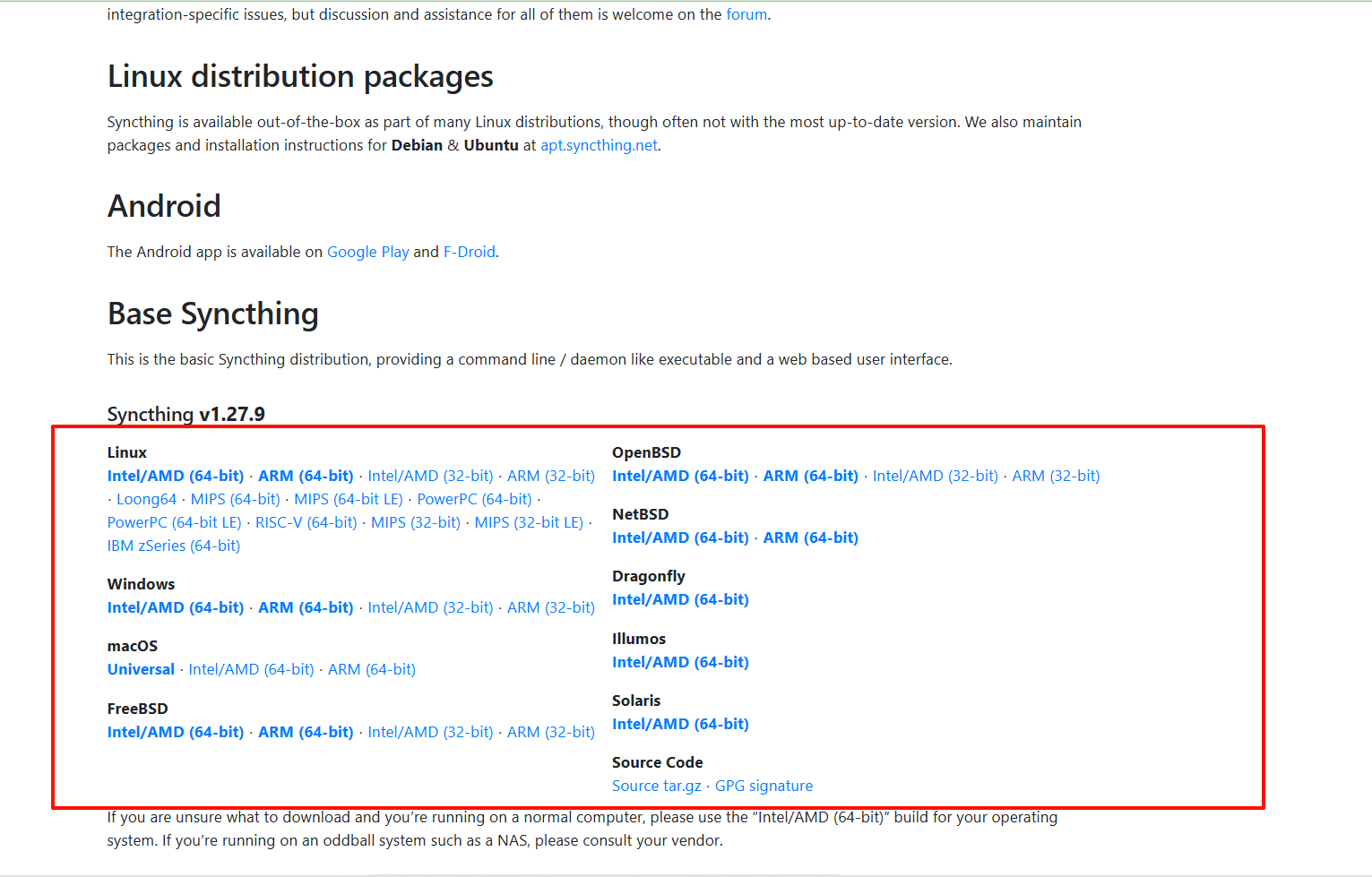
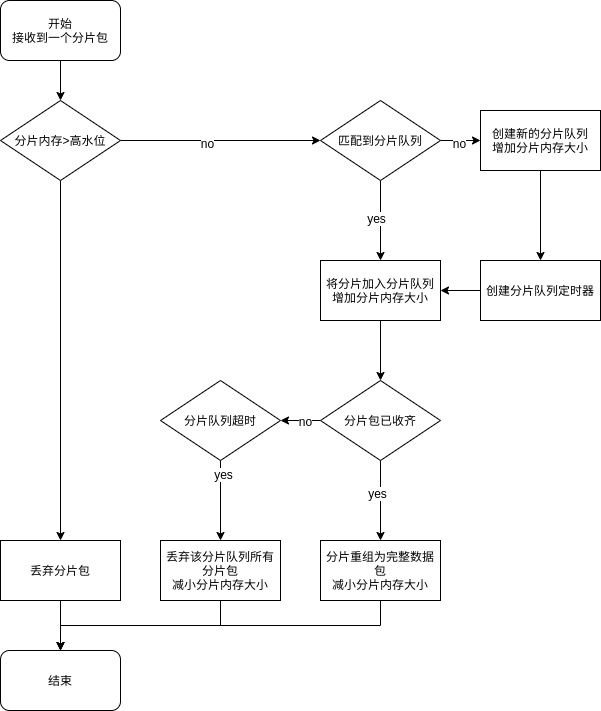
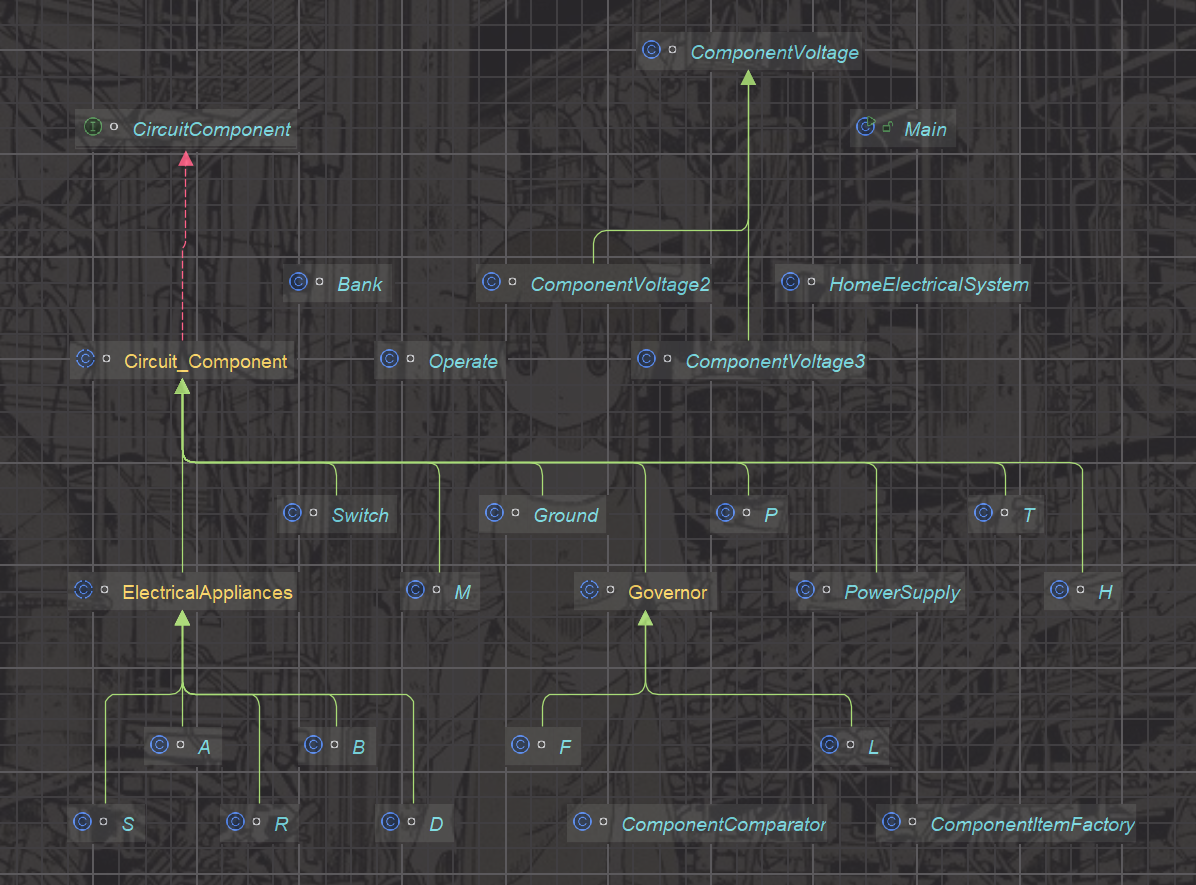
树上随机游走

问题描述

给定一颗树，树上有一点，每一时刻都会等概率地移动至邻接节点上，求该点移动至某一点的期望距离。

定义

$ T = (V,E) : $ 所讨论的树；
$ d(u) : u$ 节点的度数；
$ w(u,v) : u$ 结点与 $ v $ 结点之间的边的边权；
$ size(u) : u$ 结点的子树大小；
$ p_u : u$ 结点的父节点；
$ son_u : u$ 结点的子节点集合；
$ sibling_u : u$ 结点的兄弟结点集合。

向父结点走的期望距离

设 $ f(u) $ 代表 $ u $ 结点走到其父结点 $ p_u $ 的期望距离，则有：

\[\begin{aligned}

f(u) &= \frac{w(u, p_u) + \sum_{v \in son_u }(w(u, v) + f(v) + f(u))}{d(u)}

\end{aligned}\]

分子中的前半部分代表直接走向了父结点的距离；后半部分代表先走向了子结点，再由子结点走回来然后再向父结点走的距离。

从 $u$ 结点走向其任何邻接点的概率相同，所以总体除以 $d(u)$。

将上式右边和式中的 $f(u)$ 提出来：

\[\begin{aligned}

f(u) &= \frac{w(u, p_u) + (d(u) - 1) \cdot f(u) + \sum_{v \in son_u}{(w(u, v) + f(v))}}{d(u)}

\end{aligned}\]

两边同乘 $d(u)$，则有：

\[\begin{aligned}

d(u) \cdot f(u) &= w(u, p_u) + \sum_{v \in son_u }(w(u, v) + f(v)) + (d(u) - 1)\cdot f(u)

\end{aligned}\]

两边同减 $(d(u) - 1) \cdot f(u)$ 得：

\[\begin{aligned}

f(u) &= w(u, p_u) + \sum_{v \in son_u }(w(u, v) + f(v))

\end{aligned}\]

再将权值，即 $w$ 整合至一个和式得：

\[\begin{aligned}

f(u) &= \sum_{(u, s) \in E} w(u, s) + \sum_{v \in son_u } f(v)

\end{aligned}\]

我们将这个式子设为 $(1)$ 式，下文需要用到。

叶结点的初始值为 $1$，即 $f(leaf) = 1$（因为它只能直接向父结点走）。

特别地，当边权全部为 $1$ 时，上式可化简为：

\[\begin{aligned}

f(u) &= d(u) + \sum_{v \in son_u} f(v)

\end{aligned}\]

即 $u$ 子树的所有结点的度数和，同时也是 $2 \cdot size(u) - 1$，因为除 $u$ 与 $p_u$ 之间的边只有 $1$ 点贡献以外，每条边会产生 $2$ 点度数的贡献（一去一回走两次），而每个结点连向其父亲的边有且只有一条，所以就是 $2 \cdot size(u) - 1$。

向子节点走的期望距离

我们再设 $g(u)$ 代表从 $u$ 结点的父节点 $p_u$ 走到 $u$结点的期望距离。注意看清楚，$g(u)$ 不是代表从 $u$ 结点走向其子结点的期望距离。

易得：

\[\begin{aligned}

g(u) &= \frac{w(u, p_u) + w(p_u,p_{p_u}) + g(p_u) + g(u) + \sum_{v \in sibling_u}{(w(p_u, v) + f(v) + g(u))}}{d(p_u)}

\end{aligned}\]

分子中的第一部分代表从 $p_u$ 直接走向了结点 $u$；第二部分代表先走向了 $p_{p_u}$ 再走回来，然后再向 $u$ 结点走；第三部分代表先走向 $u$ 结点的兄弟结点再走回来，然后再向 $u$ 结点走。

从 $p_u$ 结点走向其任何邻接点的概率相同，所以总体再除以 $d(p_u)$。

上式左右两边同乘 $d(p_u)$ 得：

\[\begin{aligned}

d(p_u) \cdot g(u) &= w(u, p_u) + w(p_u,p_{p_u}) + g(p_u) + g(u) + \sum_{v \in sibling_u}{(w(p_u, v) + f(v) + g(u))}

\end{aligned}\]

右边和式中共有 $d(p_u) - 2$ 个 $g(u)$，和式外还有一个 $d(u)$，所以等式左右两边同时减去 $(d(p_u) - 1) \cdot g(u)$ 得：

\[\begin{aligned}

g(u) &= w(u, p_u) + w(p_u,p_{p_u}) + g(p_u) + \sum_{v \in sibling_u}{(w(p_u, v) + f(v))}

\end{aligned}\]

将所有的权值，即 $w$ 合并到一个和式，得：

\[\begin{aligned}

g(u) &= g(p_u) + \sum_{(p_u, s) \in E} w( p_u, s) + \sum_{v \in sibling_u} f(v)

\end{aligned}\]

我们将这个式子设为 $(2)$ 式，下文也需要用到。

再将刚刚得到的 $(1)$ 式：

\[\begin{aligned}

f(u) &= \sum_{(u, s) \in E} w(u, s) + \sum_{v \in son_u } f(v)

\end{aligned}\]

转化成

\[\begin{aligned}

\sum_{(p_u, s) \in E} w(p_u, s) + \sum_{v \in sibling_{u} } f(v) + f(u) &= f(p_u)

\end{aligned}\]

即

\[\begin{aligned}

\sum_{(p_u, s) \in E} w(p_u, s) + \sum_{v \in sibling_{u} } f(v) &= f(p_u) - f(u)

\end{aligned}\]

再带入 $(2)$ 式得：

\[\begin{aligned}

g(u) &= g(p_u) + f(p_u) - f(v)

\end{aligned}\]

根节点的初始值设为 $0$，即 $g(root) = 0$。

下面是代码（以无权树为例）

void dfs1(int u, int p_u) {
    f[u] = edge[u].size();
    for (int i = 0; i < edge[u].size(); ++ i) {
        int v = edge[u][i];
        if (v == p_u)
            continue;
        dfs1(v, u);
        f[u] += f[v];
    }
}

void dfs2(int u, int p_u) {
    if(u != root)//root 一般为 1
        g[u] = g[p_u] + f[p_u] - f[u];
    for(int i = 0; i < edge[u].size(); ++ i) {
        int v = edge[u][i];
        if(v == p_u)
            continue;
        dfs2(v, u);
    }
}