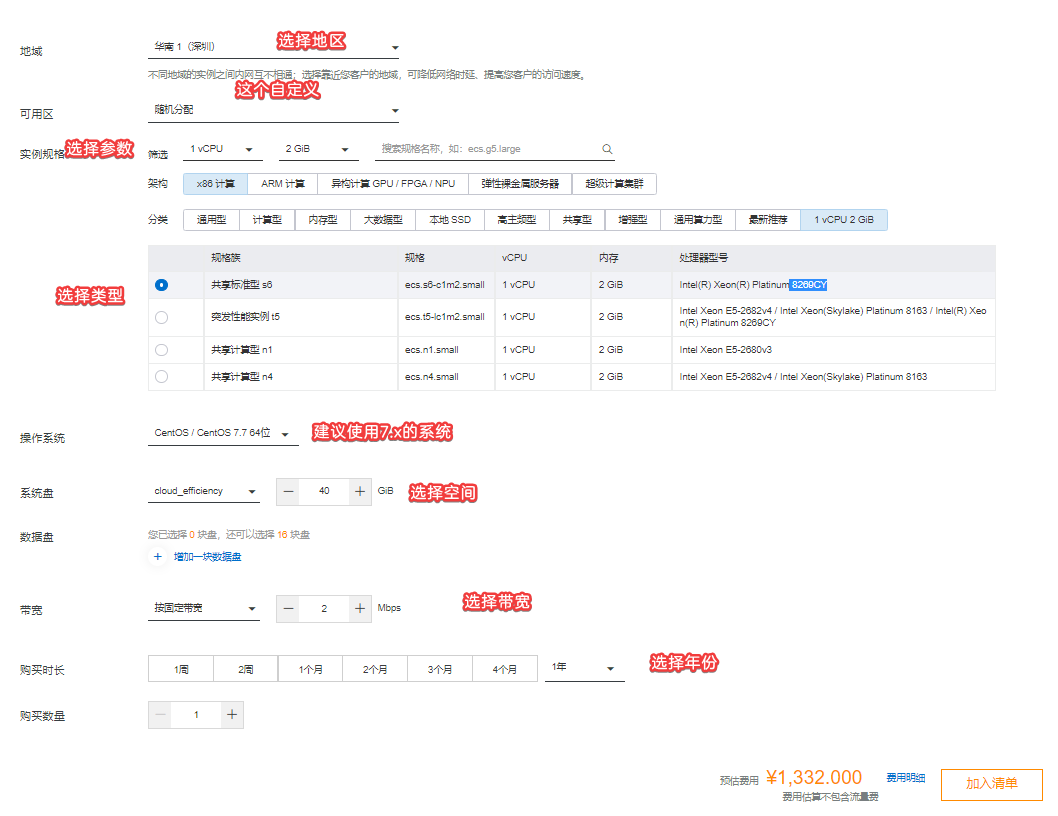
贝叶斯滤波预测方程与观测方程：

其中：\(X_k, X_{k-1}, Y_k, Q_k, R_k\)都是随机变量

推出了贝叶斯滤波的三个公式

1. 预测步

   \[f_k^{-}(x)=\int_{-\infty}^{+\infty}f_{Q_k}[x-f(v)]f_{k-1}^{+}(v)dv
   \]

2. 更新步

   \[f_k^+(x)=\eta_k \cdot f_{R_k}[y_k-h(x)]\cdot f_k^-(x)
   \]
   \[\eta_k = (\int_{-\infty}^{+\infty}f_{R_k}[y_1-h(x)]\cdot f_k^-(x)dx)^{-1}
   \]

相比于贝叶斯滤波，卡尔曼滤波多了几个假设：

1. 卡尔曼滤波假设$ f(X_{k-1})
   \(,\)h(X_k)$是线性的

   \[f(X_{k-1})=F\cdot X_{k-1}
   \]
   \[h(X_{k})=H(X_{k})
   \]

2. \(Q_k, R_k\)都是正态分布

   \[f_{Q}(x)=(2\pi Q)^{-\frac{1}{2}}e^{-\frac{x^2}{2Q}}

   \qquad Q \backsim N(0, Q)
   \]

   \[f_R(x)=(2\pi R)^{-\frac{1}{2}}e^{-\frac{x^2}{2R}}
   \qquad R \backsim N(0, R)
   \]

下面来推导卡尔曼滤波：

设\(X_{k-1} \backsim N(\mu_{k-1}^{+}, \sigma_{k-1}^{+})\)

1. 预测步

   \[\begin{equation}
   \begin{aligned}

   f_k^{-}(x)&

   =\int_{-\infty}^{+\infty}f_{Q_k}[x-f(v)]f_{k-1}^{+}(v)dv \\&
   =\int_{-\infty}^{+\infty}(2\pi Q)^{-\frac{1}{2}} e^{-\frac{(x-Fv)^2}{2Q}} \cdot (2\pi \sigma_{k-1}^{+})^{-\frac{1}{2}}e^{-\frac{(v-\mu_{k-1}^{+})^2}{2\sigma_{k-1}^{+}}}dv \\&
   \implies N \backsim (F\mu_{k-1}^{+},F^2\sigma_{k-1}+Q)

   \end{aligned}
   \end{equation}
   \]

   这个公式比较难算，推荐：

   1. 数学软件，mathematica
   2. 复变函数，留数定理计算
   3. 傅里叶变换+卷积计算
      设\(f_k^{-}(x)\)，这样就得到了卡尔曼滤波的前两个方程：
   \[\mu_k^-=F\mu_{k-1}^+
   \]
   \[\sigma_k^-=F^2\sigma_{k-1}^-+Q
   \]

2. 更新步

   \[f_k^{-}(x)\backsim N(\mu_k^-, \sigma_k^-)
   \]
   \[\begin{equation}
   \begin{aligned}

   f_k^+(x)&
   =\eta f_R(y_k-h\cdot x)\cdot f_k^-(x)\\&
   =\eta (2\pi R)^{-\frac{1}{2}} e^{-\frac{(y_k - h\cdot x)^2}{2R}}\cdot (2\pi \sigma_k^-)^{-\frac{1}{2}}e^{-\frac{(x-\mu_k^-)^2}{2\sigma_k^-}}

   \end{aligned}
   \end{equation}

   \]

   \[\eta = (\int_{-\infty}^{+\infty}(2\pi R)^{-\frac{1}{2}} e^{-\frac{(y_k - h\cdot x)^2}{2R}}\cdot (2\pi \sigma_k^-)^{-\frac{1}{2}}e^{-\frac{(x-\mu_k^-)^2}{2\sigma_k^-}}dx)^{-1}
   \]

   使用数学软件，可以得出：

   \[X_k^+ \backsim N(\frac{h\sigma_k^{-}y_{k} + R\mu_k^-}{h^2\sigma_k^- + R}, \frac{R\sigma_k^-}{h^2\sigma_k^-+R})
   \]

   假设\(X_K^+\backsim N(\mu_K^+, \sigma_k^+)\),我们就得到了卡尔曼滤波的后三个公式：

   \[\begin{equation}
   \begin{aligned}

   \mu_k^+ &
   = \frac{h\sigma_k^-}{h^2\sigma_k^-+R}y_k+\frac{\mu_k^-(R+h^2\sigma_k^-) - \mu_k^-h^2\sigma_k^-}{h^2\sigma_k^-+R} \\&

   = \frac{h\sigma_k^-}{h^2\sigma_k^-+R}(y_k-h\mu_k^-)+\mu_k^-

   \end{aligned}
   \end{equation}
   \]

   \[\begin{equation}
   \begin{aligned}

   \sigma_k^+&

   =\frac{R\sigma_k^-}{h^2\sigma_k^-+R}\\&
   =\frac{\sigma_k^-(R+h^2\sigma_k^-) - \sigma_k^-h^2\sigma_k^-}{h^2\sigma_k^-+R}\\&

   =(1-\frac{h^2\sigma_k^-}{h^2\sigma_k^-+R})\sigma_k^-
   \end{aligned}
   \end{equation}
   \]

   \[K=\frac{h^2\sigma_k^-}{h^2\sigma_k^-+R}
   \]

卡尔曼滤波的5个公式总结：

公式(1)：预测均值，也就是预测的状态量；

公式(2)：预测的状态量的方差，也就是预测步的噪声，或者预测的可信度；

公式(3)：卡尔曼增益

公式(4)：观测更新的均值，也是k时刻输出的状态量；

公式(5)：观测更新的均值，也是k时刻输出的状态量；

\(Q\)为预测噪声，\(R\)为观测噪声。\(K\)也叫做卡尔曼增益。观察它的公式，不难看出，

当\(R \gg h^2\sigma_k^-\)时候，\(K\to 0\),\(\mu_k^+=\mu_k^- + K(y_k - h \mu_k^-)=\mu_k^-\)，这时候更加相信预测。

当\(R \ll h^2\sigma_k^-\) 时候，$ K\to\frac{1}{h}$, \(\mu_k^+=\mu_k^- + \frac{(y_k - h \mu_k^-)}{h}=\frac{y_k}{h}\)，$ y_k=hx_k+R $， 由于 $ R $ 较小，所以我们这时候更倾向于相信观测，这是十分合理的。

接下来看一下矩阵形式的卡尔曼滤波

\(\mu_k \to \vec \mu_k\), \(\sigma_k \to \sum_k\)协方差矩阵，\(F\)和\(H\)皆为矩阵。\(Q\)为预测噪声，\(R\)为观测噪声

类推一下