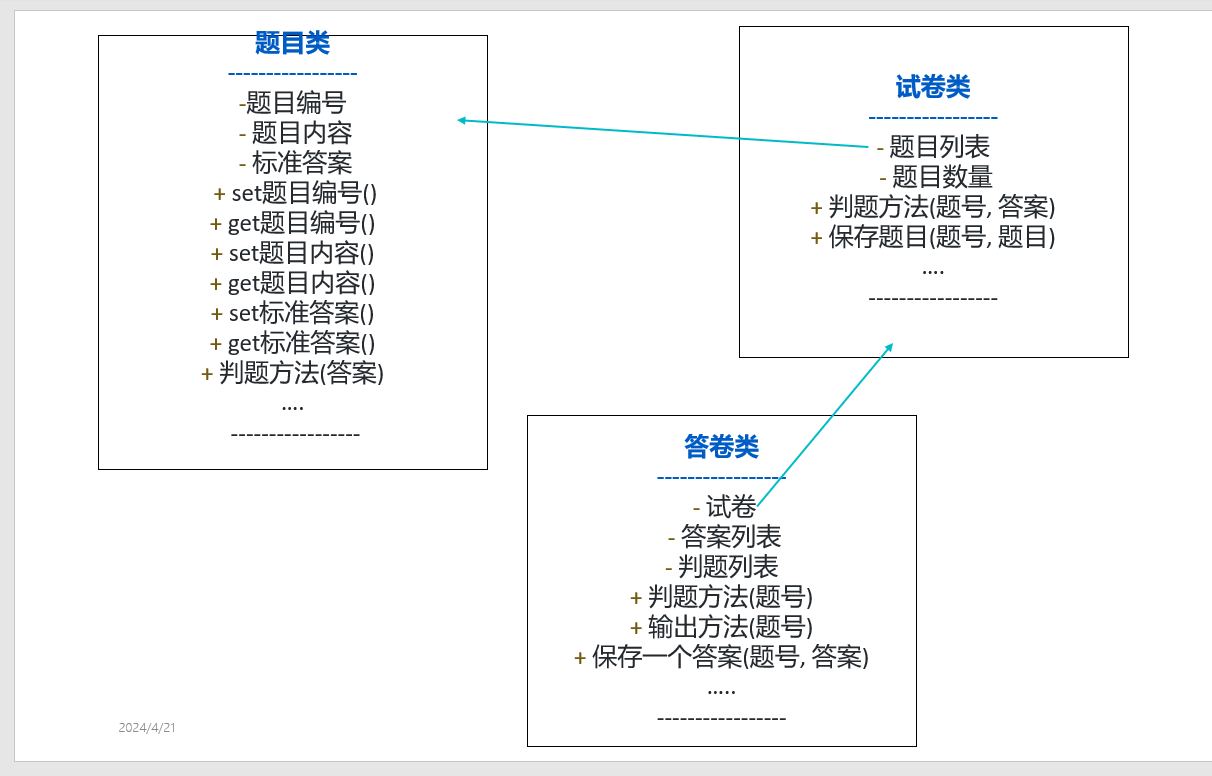
本质矩阵的内在性质和本质矩阵的分解

1.0 概述

\(\quad\)我们在前面的文章中已经分析过对极几何约束，并且详细的推导了对极几何是怎么来的，但是对其中的一些关于本质矩阵的性质，我们只是一笔代过，并没有做详细的分析，这里主要对本质矩阵的一些性质以及本质矩阵的分解结果做出详细的讨论和推导。

本质矩阵：

\[E=t^{\wedge }R
\]

2.0 特征值分解

2.1 特征值和特征向量的几何意义

\(\quad\)矩阵和向量作乘法，向量会变成另一个方向或长度的新向量，主要会发生旋转、伸缩的变化如果矩阵乘以某些向量后，向量不发生旋转变换，只产生伸缩变换那么就说这些向量是矩阵的特征向量，伸缩的比例就是特征值。

2.2 特征值和特征向量的数学描述

\(\quad\)如果 \(A\) 是 \(n\) 阶方阵，数 \(λ\) 和 \(n\) 维非零列向量 \(x\) 是 \(A\) 的对应于特征值的特征向量，有：

\[Ax=\lambda x
\]

\(\quad\)也可以写成：

\[(A-\lambda E)x=0
\]

2.3 特征值分解

特征值分解就是将一个矩阵分解成：

\[A=P\Lambda P^{-1}
\]

\(P\) 是这个矩阵 \(A\) 的特征向量组成的矩阵。
\(Λ\) 是特征值组成的对角矩阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向。

2.4 特征值分解的过程

解下面的线性方程组：

\[|A-\lambda E|=0
\]

可以解出 \(n\) 个特征值：\(\lambda_1,\lambda_2,\lambda_3, \dots \lambda_n\)。

再把 \(n\) 个特征值代入下面的式子：

\[(A-\lambda E)x=0
\]

可以求出 \(n\) 个对应的特征向量：\(P_1,P_2,P_3,\dots P_n\)。
对于每一个特征值与特征向量满足：

\[Ax_i=\lambda _i
\]

令：

\[P=\begin{pmatrix}
x_1 & x_2 & x_2 & x_2& \dots &x_n\\
\end{pmatrix} \\
\Lambda = \begin{bmatrix}
\lambda _1 & & & \\
& \ddots & & \\
& & \ddots & \\
& & & \lambda _n
\end{bmatrix}
\]

对于 \(n\) 个特征值和特征向量可写成：

\[\begin{array}{l}
{\left[\begin{array}{llll}
A \boldsymbol{x}_{1} & A \boldsymbol{x}_{2} & \ldots & A \boldsymbol{x}_{n}
\end{array}\right]=A\left[\begin{array}{llll}
\boldsymbol{x}_{1} & \boldsymbol{x}_{2} & \ldots & \boldsymbol{x}_{n}
\end{array}\right]=A P} \\
{\left[\begin{array}{llll}
\lambda_{1} \boldsymbol{x}_{1} & \lambda_{2} \boldsymbol{x}_{2} & \ldots & \lambda_{n} \boldsymbol{x}_{n}
\end{array}\right]=\left[\begin{array}{llll}
\boldsymbol{x}_{1} & \boldsymbol{x}_{2} & \ldots & \boldsymbol{x}_{n}
\end{array}\right]\left[\begin{array}{lll}
\lambda_{1} & & \\
& \ddots & \\
& & \lambda_{n}
\end{array}\right]=P \Lambda}
\end{array}
\]

可得:

\[AP=P\Lambda \\
A=P\Lambda P^{-1}
\]

3.0 本质矩阵性质

3.1 自由度

本质矩阵由 \(t\) 和 \(R\) 组成，本身应该有 \(6\) 个自由度，平移和旋转各三个，但是由于对极约束中的尺度等价性的存在，退化成了 \(5\) 个自由度。
且由于 \(t^{\wedge}\) 的行列式为 \(0\)，即 \(det([t]^{\wedge})=0\)，所以 \(Rank([t]^{\wedge})=2\)，因此有 \(det(E)=0\)，\(Rank(E)=2\)。

3.2 本质矩阵奇异值的形式

\(\quad\)根据 \(E = t^{\wedge}R\)，可以证明，本质矩阵 \(E\) 的奇异值必定是 \([\sigma,\sigma,0] ^T\) 的形式，这称为本质矩阵的内在性质。下面对该性质进行证明。

\(\quad\)对 \(E\) 的奇异值分解可以由对 \(E E^T\) 的特征值分解得到，E 的奇异值分解的最终形式为

\[E=U\Sigma V^T
\]

\(\quad\)对 \(EE^T\) 为:

\[\begin{array}{c}
EE^T=U\Sigma V^TV\Sigma ^TU^T \\
EE^T=U\Sigma \Sigma ^TU^T
\end{array}
\]

\(\quad\) 设 \(\Sigma \Sigma ^T = M\) ，则：

\[\begin{array}{c}
EE^T=UMU^T
\end{array}
\]

\(\quad\)也就是说对 \(EE^T\) 进行特征值分解可以得到 \(U,M\)（特征值组成的对角阵），对 \(M\) 对角线上的特征值开方即可得到 \(\Sigma\)。

\(\quad\)所以我们的步骤为：

求 \(EE^T\)
求 \(EE^E\) 的特征值分解得到 \(U,M\)
对 M 的对角线上的特征值开根号得到 \(\Sigma\) ，并查看其中的 \(\sigma_i\) 是否符合 \([\sigma,\sigma,0]\)的形式。

1.0 求解 \(EE^T\)

\[\begin{array}{l}
E=t^{\wedge} R \\
E E^{\top}=t^{\wedge} R\left(t^{\wedge} R\right)^{\top} \\
=t^{\wedge} R R^{\top} t^{\wedge \top} \quad\left(R \text { 是旋轻矩阵，故也是正交矩阵，故 } R R^{\top}=I\right) \\
=t^{\wedge} t^{\wedge \top} \\
\end{array}
\]

2.0 特征值分解

\[t=\left[\begin{array}{l}a_{1} \\ a_{2} \\ a_{3}\end{array}\right] \quad \Rightarrow t^{\wedge}=\left[\begin{array}{ccc}0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0\end{array}\right]
\]

把 \(t\) 规范化为长度为 \(1\)，所以 \(t_1^2 + t_2^2 + t_3^2 = 1\)。（对极约束为0，尺度等价）

\[\begin{aligned}
E E^{\top} & =t^{\wedge} t^{\wedge} \\
& =\left[\begin{array}{ccc}
0 & -a_{3} & a_{2} \\
a_{3} & 0 & -a_{1} \\
-a_{2} & a_{1} & 0
\end{array}\right]\left[\begin{array}{ccc}
0 & a_{3} & -a_{2} \\
-a_{3} & 0 & a_{1} \\
a_{2} & -a_{1} & 0
\end{array}\right] \\
& =\left[\begin{array}{ccc}
a_{3}^{2}+a_{2}^{2} & -a_{1} a_{2} & -a_{1} a_{3} \\
-a_{1} a_{2} & a_{1}^{2}+a_{3}^{2} & -a_{2} a_{3} \\
-a_{1} a_{3} & -a_{2} a_{3} & a_{2}^{2}+a_{1}^{2}
\end{array}\right]
\end{aligned}
\]

求特征值：

\[\begin{array}{l}
\left(E E^{\top}-\lambda I\right) x=0 \text { 即 }\left|E E^{\top}-\lambda I\right|=0 \\
\Rightarrow\left|\begin{array}{ccc}
a_{3}^{2}+a_{2}^{2}-\lambda & -a_{1} a_{2} & -a_{1} a_{3} \\
-a_{1} a_{2} & a_{1}^{2}+a_{3}^{2}-\lambda & -a_{2} a_{3} \\
-a_{1} a_{3} & -a_{2} a_{3} & a_{1}^{2}+a_{2}^{2}-\lambda
\end{array}\right|=0 \\
\Rightarrow\left|\begin{array}{ccc}
1-\lambda-a_{1}^{2} & -a_{1} a_{2} & -a_{1} a_{3} \\
-a_{1} a_{2} & 1-\lambda-a_{2}^{2} & -a_{2} a_{3} \\
-a_{1} a_{3} & -a_{2} a_{3} & 1-\lambda-a_{3}^{2}
\end{array}\right|=0 \\
\end{array}
\]

\[\begin{aligned}
& \left(1-\lambda-a_{1}^{2}\right)\left(1-\lambda-a_{2}^{2}\right)\left(1-\lambda-a_{3}^{2}\right)-a_{1}^{2} a_{2}^{2} a_{3}^{2}-a_{1}^{2} a_{2}^{2} a_{3}^{2} \\
& -\left(1-\lambda-a_{2}^{2}\right) a_{1}^{2} a_{3}^{2}-\left(1-\lambda-a_{3}^{2}\right) a_{1}^{2} a_{2}^{2}-\left(1-\lambda-a_{1}^{2}\right) a_{2}^{2} a_{3}^{2} \\
= & \left((1-\lambda)^{2}-(1-\lambda) a_{2}^{2}-(1-\lambda) a_{1}^{2}+a_{1}^{2} a_{2}^{2}\right)\left(1-\lambda-a_{3}^{2}\right)-a_{1}^{2} a_{2}^{2} a_{3}^{2}-a_{1}^{2} a_{2}^{2} a_{3}^{2} \\
& -\left(1-\lambda-a_{2}^{2}\right) a_{1}^{2} a_{3}^{2}-\left(1-\lambda-a_{3}^{2}\right) a_{1}^{2} a_{2}^{2}-\left(1-\lambda-a_{1}^{2}\right) a_{2}^{2} a_{3}^{2} \\
= & (1-\lambda)^{3}-(1-\lambda)^{2} a_{2}^{2}-(1-\lambda)^{2} a_{1}^{2}+(1-\lambda)\left(a_{1}^{2} a_{2}^{2}-(1-\lambda)^{2} a_{3}^{2}+(1-\lambda) a_{2}^{2} a_{3}^{2}\right. \\
& +\left(1-\lambda a_{1}^{2} a_{3}^{2}-a_{1}^{2} a_{2}^{2} a_{3}^{2}-a_{1}^{2}\left(a_{2}^{2} a_{3}^{2}-a_{1}^{2} a_{2}^{2} a_{3}^{2}\right.\right. \\
& -\left(1-\lambda-a_{2}^{2}\right) a_{1}^{2} a_{3}^{2}-\left(1-\lambda-a_{3}^{2}\right) a_{1}^{2} a_{2}^{2}-\left(1-\lambda-a_{1}^{2}\right) a_{2}^{2} a_{3}^{2} \\
= & (1-\lambda)^{3}-(1-\lambda)^{2} a_{2}^{2}-(1-\lambda)^{2} a_{1}^{2}-(1-\lambda)^{2} a_{3}^{2} \\
= & (1-\lambda)^{3}-(1-\lambda)^{2} \\
= & (1-\lambda)^{2}(1-\lambda-1) \\
= & (1-\lambda)^{2}(-\lambda)=0
\end{aligned}
\]

解得:

\[\lambda_1 = \lambda_2 = 1, \lambda_3=0
\]

这里等于 \(1\) 的原因是因为我们假设 \(t\) 的模长为 \(1\)

最终开根号可以得到形如 \([\lambda,\lambda,0]\)的形式。

4.0 本质矩阵分解后的结果为什么有四种

旋转矩阵的伴随性质，后面会用到:

\[\begin{aligned}
& (\mathbf{R v})^{\wedge}=\mathbf{R} \mathbf{v}^{\wedge} \mathbf{R}^{T} \\
\Leftrightarrow & (\mathbf{R v})^{\wedge} \mathbf{R}=\mathbf{R} \mathbf{v}^{\wedge} \\
\Leftrightarrow & \forall \mathbf{u} \in \mathbb{R}^{3},(\mathbf{R v})^{\wedge} \mathbf{R u}=\mathbf{R } \mathbf{v}^{\wedge} \mathbf{u} \\
\Leftrightarrow & \mathbf{u} \in \mathbb{R}^{3},(\mathbf{R v}) \times(\mathbf{R u})=\mathbf{R}(\mathbf{v} \times \mathbf{u})
\end{aligned}
\]

所以上面是一直等价的（倒数第二个式子到最后一个式子等价，因为矩阵乘法满足结合律），我们只需要证明最后一个式子即可，最后一个式子通过利用向量叉乘的旋转变换不变性（参照Wikipedia）。

其实最后一个式子很好理解，对于任意\(v,u∈\mathbf{R}^3v,u∈\mathbf{R}^3\)，它们是任意三维向量，将他们经过同一个旋转，它们的相对位姿与模长都不会改变，所以 \(Rv\) 与 \(Ru\)的叉乘仍然是相对它们垂直、大小也不变的三维向量。

\(\quad\) 先来看14讲中的说明，比较简单的概括

我们知道 \(\Sigma = diag(\sigma, \sigma, 0)\)。在 \(SVD\) 分解中，对于任意的一个 \(E\) ,存在两个可能的 \(t, R\) 与之对应：

\[\begin{array}{l}
\boldsymbol{t}_{1}^{\wedge}=\boldsymbol{U} \boldsymbol{R}_{Z}\left(\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}_{1}=\boldsymbol{U} \boldsymbol{R}_{Z}^{T}\left(\frac{\pi}{2}\right) \boldsymbol{V}^{T} \\
\boldsymbol{t}_{2}^{\wedge}=\boldsymbol{U} \boldsymbol{R}_{Z}\left(-\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}_{2}=\boldsymbol{U} \boldsymbol{R}_{Z}^{T}\left(-\frac{\pi}{2}\right) \boldsymbol{V}^{T} .
\end{array}
\]

其中 \(\boldsymbol{R}_{Z}\left(\frac{\pi}{2}\right)\) 表示沿 \(Z\) 轴旋转 \(90\) 度得到的旋转矩阵。同时, 由于 \(-\boldsymbol{E}\) 和 \(\boldsymbol{E}\) 等价, 所以对任意一个 \(t\) 取负号, 也会得到同样的结果。因此, 从 \(\boldsymbol{E}\) 分解到 \(\boldsymbol{t}, \boldsymbol{R}\) 时, 一共存在四个可能的解。

这里笔者本身是比较蒙的，负号的等价性还可以理解，直接乘过去对极约束相当于是乘了个 \(-1\)，当然也是满足的，但是两对解是怎么来的还是比较模糊的，下面我们对其进行说明。

\(\quad\)其实 \(\Sigma\) 是可以分成两个矩阵相乘的形式

\[\begin{array}{l}
\Sigma=\left[\begin{array}{lll}
a & 0 & 0 \\
0 & a & 0 \\
0 & 0 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & a & 0 \\
-a & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\\
\begin{array}{c}
E=U\left[\begin{array}{lll}
a & 0 & 0 \\
0 & a & 0 \\
0 & 0 & 0
\end{array}\right] V^{T}=U\left[\begin{array}{ccc}
0 & a & 0 \\
-a & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] V^{T} \\
=U\left[\begin{array}{ccc}
0 & a & 0 \\
-a & 0 & 0 \\
0 & 0 & 0
\end{array}\right] U^{T} U\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] V^{T}=[\boldsymbol{t}]^{\wedge} R \\
{\left[\boldsymbol{t}_{1}\right]^{\wedge}=U\left[\begin{array}{ccc}
0 & a & 0 \\
-a & 0 & 0 \\
0 & 0 & 0
\end{array}\right] U^{T}=\left[U\left[\begin{array}{l}
0 \\
0 \\
a
\end{array}\right]\right]^{\wedge}} \\
\boldsymbol{t}_{1}=U\left[\begin{array}{l}
0 \\
0
\end{array}\right]=\left[\begin{array}{lll}
U_{0} & U_{1} & U_{2}
\end{array}\right]\left[\begin{array}{l}
0 \\
0 \\
a
\end{array}\right]=U_{2} a \\
R_{1}=U\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] V^{T} \triangleq U W V^{T}
\end{array}
\end{array}
\]

同样 \(\Sigma\) 还有另外一种分解方式：

\[\begin{array}{c}
\Sigma=\left[\begin{array}{lll}
a & 0 & 0 \\
0 & a & 0 \\
0 & 0 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & -a & 0 \\
a & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\left[\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] \\
\boldsymbol{t}_{2}=U\left[\begin{array}{c}
0 \\
0 \\
-a
\end{array}\right]=-U_{2} a=-\boldsymbol{t}_{1} \\
R_{2}=U\left[\begin{array}{ccc}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] V^{T} \triangleq U W^{T} V^{T}
\end{array}
\]

除此之外我们再无其他分解了，容易看出这两种解有这样的关系：

\(\boldsymbol{t}_{2}=-\boldsymbol{t}_{1}\)
\(R_{2}\) 是 \(R_{1}\) 绕 \(\boldsymbol{t}\) (平移向量) 轴旋转 \(\pi\) 弧度;

这两种分解通常这样表示:

\[\begin{array}{l}
\boldsymbol{t}_{1}^{\wedge}=\boldsymbol{U} \boldsymbol{R}_{Z}\left(\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}_{1}=\boldsymbol{U} \boldsymbol{R}_{Z}^{T}\left(\frac{\pi}{2}\right) \boldsymbol{V}^{T} \\
\boldsymbol{t}_{2}^{\wedge}=\boldsymbol{U} \boldsymbol{R}_{Z}\left(-\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}_{2}=\boldsymbol{U} \boldsymbol{R}_{Z}^{T}\left(-\frac{\pi}{2}\right) \boldsymbol{V}^{T} .
\end{array}
\]

其中 \(R_{z}\left(+\frac{\pi}{2}\right)\) 表示绕 \(z\) 轴旋转90度得到的旋转矩阵。

\[R_{z}\left(+\frac{\pi}{2}\right)=\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]
\]

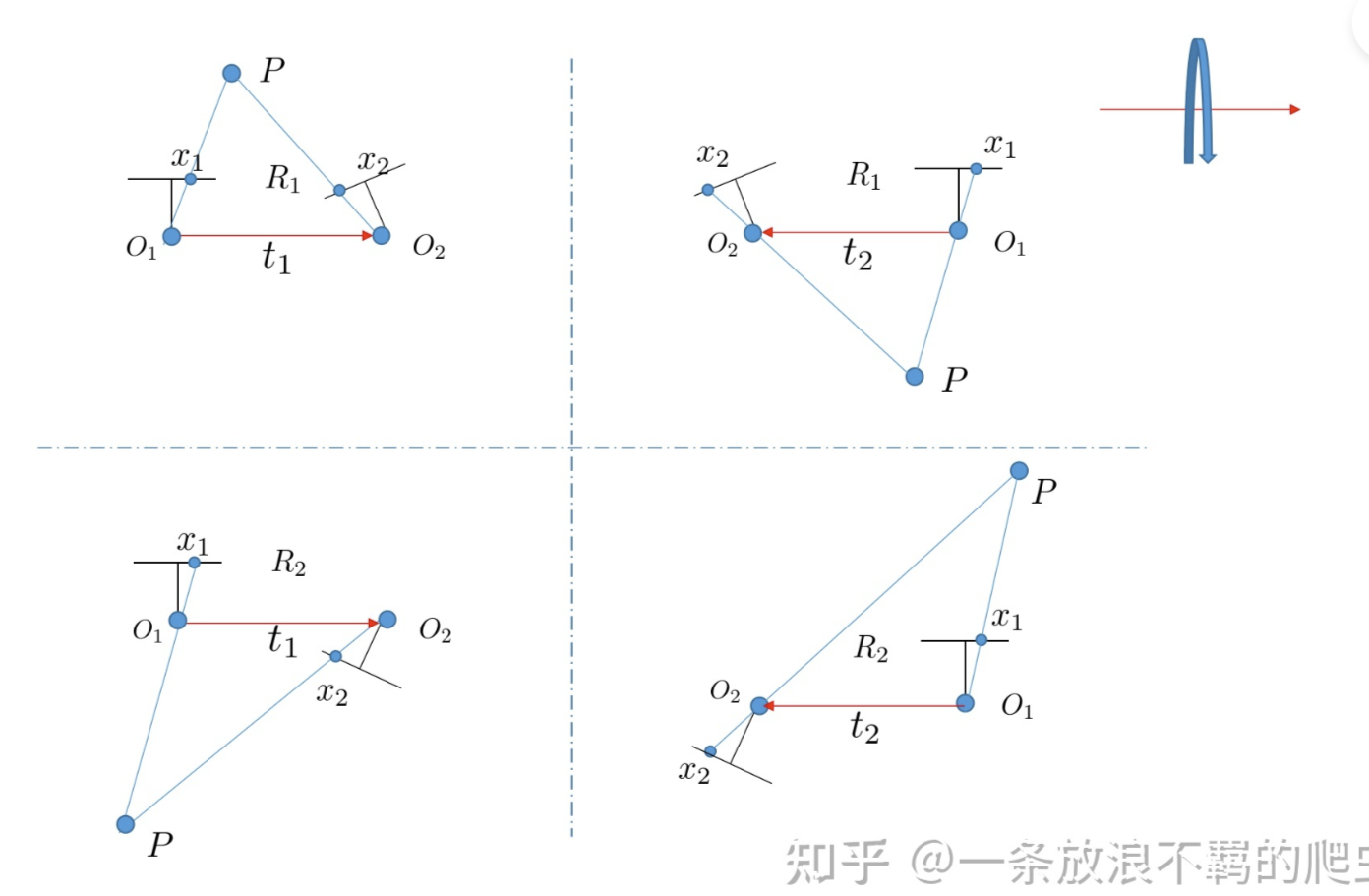
同时参考这位大佬的博客中的图对上述结果作可视化上的解释：

保持第一个相机的朝向和位置不变当做基准参考系，\(O_1,O_2\) 表示为平移量 \(t\) ， \(O_2\) 相机相对于 \(O_1\) 相机旋转过的角度为 \(R_1\) ，假设左上角第一组解 \(R_1,t_1\) 满足要求，都在相机前方；左下角的 \(R_2\) 是第二个相机绕 \(t_1\) （纸面旋转）旋转 \(\pi\) 之后得到的结果，右上角是 \(t=-t_1\) 的结果，右下角是 \(R_2,t_2\)的结果。