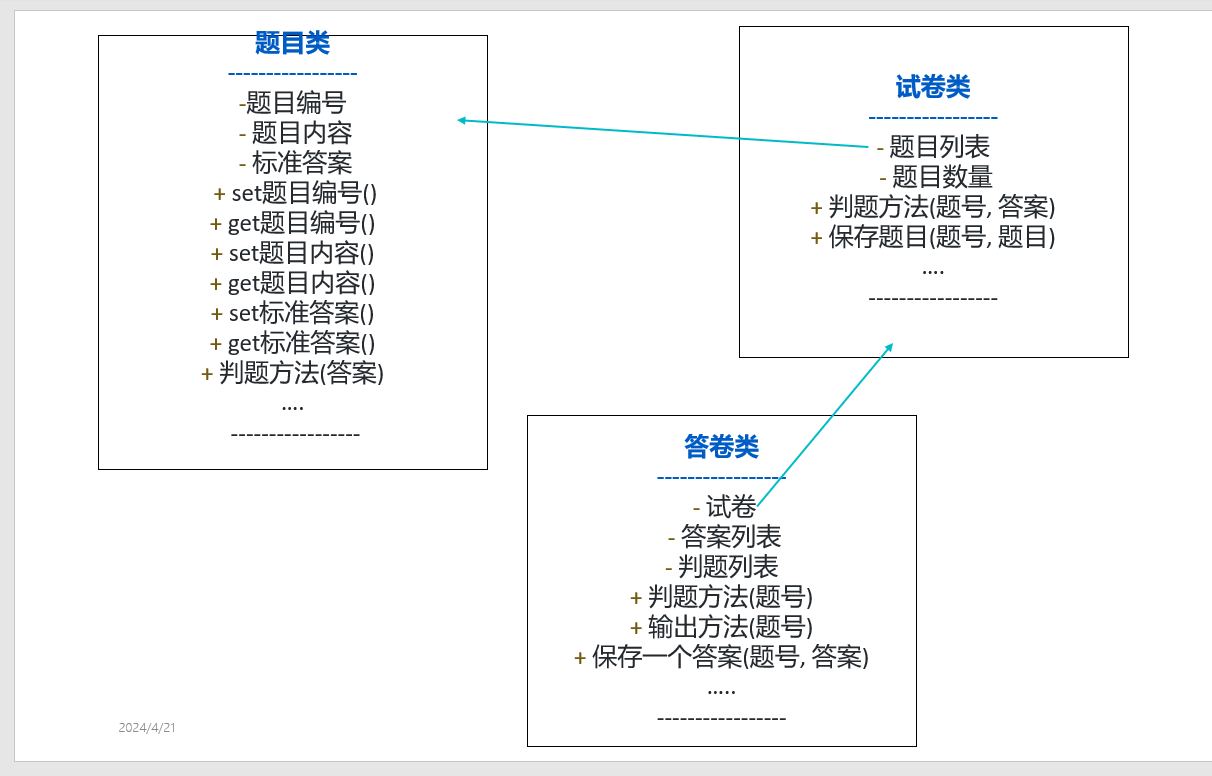
Definition. (Lebesgue outer measure)

对于任意集合 \(A \subset \mathbb{R}\) 的勒贝格外测度（Lebesgue outer measure）定义为：

同时我们称区间序列 \(\left\{ I_{n} \right\}^{\infty}_{n=1}\) 覆盖（cover）了集合 \(A\)。

Theorem 7.1

对于集合 \(A \subset \mathbb{R}\)，当且仅当 \(m^{*}(A) = 0\)，\(A\) 为一个零测集。

Proof. (Theorem 7.1)

\(\Longrightarrow\) 设 \(A \subset \mathbb{R}\) 且 \(m^{*}(A) = 0\)。由定义：

Mapping:

为一个 surjection（满射）。即对于：

（意思就是，对于每一个这种区间长度和，总能找到一个满足相同条件的区间序列，最差的情况也可以是自己。）

所以可以应用 infimum 的定义：

1. for \(~ \forall \left\{ I_{n} \right\}^{\infty}_{n=1}, ~ I_{n} \mbox{ are intervals}, ~ A \subset \bigcup\limits^{\infty}_{n=1} I_{n}: ~ \sum\limits^{\infty}_{n=1}l(I_{n}) \geq 0\)

2. for \(~ \forall \varepsilon > 0: ~ \exists \left\{ I^{'}_{n} \right\}^{\infty}_{n=1}, ~ I^{'}_{n} \mbox{ are intervals}, ~ A \subset \bigcup\limits^{\infty}_{n=1} I^{'}_{n}: ~ \sum\limits^{\infty}_{n=1} l(I^{'}_{n}) < \varepsilon\)

其中 2. 恰好满足了零测集的定义。

\(\Longleftarrow\) 设 \(A \subset \mathbb{R}\) 且 \(A\) 为零测集，由定义：

并且：\(\sum\limits^{\infty}_{n=1} l(I_{n})\) 为长度和，必有：\(\sum\limits^{\infty}_{n=1} l(I_{n}) \geq 0\)，所以：

Theorem 7.2

如果 \(A \subset B\)，那么 \(m^{*}(A) \leq m^{*}(B)\)。

Lemma.

若 \(A\subset B\)，则 \(\inf A \geq \inf B\)。

Proof. (Lemma)

由下确界定义：

又：\(A \subset B\)，则有：

所以：

由下确界定义：

假设 \(\inf A < \inf B\)，令 \(\varepsilon = \inf B - \inf A > 0\)，则：

这与： \(\forall a \in A: ~ a \geq \inf B\) 矛盾，故 \(\inf A \geq \inf B\)。

Proof. (Theorem 7.2)

设：

由于 \(A \subset B\)，则：\(A \subset B \subset \bigcup\limits^{\infty}_{n=1}J_{n}\)，\(\left\{ J_{n} \right\}^{\infty}_{n=1}\) 为以上定义的区间序列。所以包含 \(B\) 的这样的区间序列 \(\left\{ J_{n} \right\}^{\infty}_{n=1}\) 也一定包含 \(A\)。

（即：\(\left\{ J_{n} \right\}^{\infty}_{n=1}\) 一定是 \(\left\{ I_{n} \right\}^{\infty}_{n=1}\)，但\(\left\{ I_{n} \right\}^{\infty}_{n=1}\) 不一定是 \(\left\{ J_{n} \right\}^{\infty}_{n=1}\)）

所以：

由 Theorem 7.1 的证明中构造的映射，有：

which implies:

Theorem 7.3

如果 \(I\) 是一个区间，那么 \(m^{*}(I) = l(I)\)。

Proof. (Theorem 7.3)

首先，我们知道：

对于 \(\forall \sum\limits^{\infty}_{n=1}l(I_{n}), ~ I_{n} \mbox{ are intervals, } I \subset \bigcup\limits^{\infty}_{n=1}I_{n}\)：

由于 \(I \subset \bigcup\limits^{\infty}_{n=1} I_{n}\)，则 \(l(I) \leq \sum\limits^{\infty}_{n=1} l(I_{n})\)，故：

由于 \(I\) 为区间，且 \(I \subset I\)，则：

则：

所以：

• 注：这里运用到一条显然的等价条件，即：
  \[\mbox{If } ~ \forall a \in A: ~ a_{0} \leq a \; \mbox{ and } \; a_{0} \in A \quad \iff \quad \inf A = \min A = a_{0}
  \]

Theorem 7.4 (Countable subadditivity - 次可加性)

Proof. (Theorem 7.4)

由定义：

For \(\forall E_{n}\)，有：\(m^{*}(E_{n}) = \inf\left\{ \sum\limits^{\infty}_{s=1}l(I^{n}_{s}): ~ I^{n}_{s} \mbox{ 为区间, } E_{n} \subset \bigcup\limits^{\infty}_{s=1} I^{n}_{s} \right\}\)

若对于 \(\forall n \in \mathbb{N}^{+}: ~ E_{n} \subset \bigcup\limits^{\infty}_{s=1} I^{n}_{s}\)，其中\(I_{s}^{n}\) 为区间，则对于 \(\forall x \in \bigcup\limits^{\infty}_{n=1} E_{n}: ~ \exists n_{0} \in \mathbb{N}^{+}: x \in E_{n_{0}}\)，则 \(x \in \bigcup\limits^{\infty}_{s=1}I^{n_{0}}_{s}\)。

又：\(\bigcup\limits^{\infty}_{s=1}I^{n_{0}}_{s} \subset \bigcup\limits^{\infty}_{n=1}\bigcup\limits^{\infty}_{s=1} I^{n}_{s}\)，则：

因此，若对于 \(\forall n \in \mathbb{N}^{+}: ~ E_{n} \subset \bigcup\limits^{\infty}_{s=1}I^{n}_{s}\)，则有：\(\bigcup\limits^{\infty}_{n=1} E_{n} \subset \bigcup\limits^{\infty}_{n=1}\bigcup\limits^{\infty}_{s=1} I^{n}_{s}\)

设两集合：

可以发现，若视 \(B\) 中的 \(\left\{ I^{n}_{s} \right\}^{\infty, \infty}_{n=1, s=1}\) 为一个新的区间序列，且该区间序列的可数并包含了 \(\bigcup\limits^{\infty}_{n=1} E_{n}\)，这符合 \(A\) 的定义，所以：

由 (i) 中所述的满射方式，存在以下满射 \(f\) ：

而：

由 \(B \subset A\)，则 \(D \subset C\)，则：

又：\(\left\{ I^{n}_{s} \right\}^{\infty}_{s=1}\) 的选择至于条件 “\(E_{n} \subset \bigcup\limits^{\infty}_{s=1} I^{n}_{s}\)” 有关（对于每个 \(n \in \mathbb{N}^{+}\)）， 则与 \(n\) 无关，则：

• 其实这里有种更简单的证明，即直接证明以上两边相等。设：

  \[\begin{align*}
  D & = \left\{ \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}): ~ I^{n}_{s} \mbox{ 为区间, } E_{n} \subset \bigcup\limits^{\infty}_{s=1}I^{n}_{s}, ~ \bigcup\limits^{\infty}_{n=1} E_{n} \subset \bigcup\limits^{\infty}_{n=1}\bigcup\limits^{\infty}_{s=1} I^{n}_{s} \right\}\\
  D_{n} & = \left\{ \sum\limits^{\infty}_{n=1}l(I^{n}_{s}): ~ I^{n}_{s} \mbox{ 为区间, } E_{n} \subset \bigcup\limits^{\infty}_{s=1} I^{n}_{s} \right\}
  \end{align*}
  \]

  则 \(\inf{D}\) 满足：

  ① \(\sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \in D: ~ \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \geq \inf{D}\)

  ② \(\forall \varepsilon: ~ \exists \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \in D: ~ \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) < \inf{D} + \varepsilon\)

  则：

  ①

  \[\begin{align*}
  & \forall n \in \mathbb{N}^{+}: ~ \forall \sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \in D_{n}: ~ \sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \geq \inf{D_{n}}\\
  \implies & \\
  &\forall \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \in D: ~ \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \geq \sum^{\infty}_{n=1} \inf{D_{n}}
  \end{align*}
  \]

  ②

  \[\begin{align*}
  & \forall n \in \mathbb{N}^{+}: ~ \forall \varepsilon_{n} = \frac{\varepsilon}{2^{n}} > 0: ~ \exists \sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \in D_{n}: ~ \exists \sum\limits^{\infty}_{s=1} l(I^{n}_{s}) < \inf{D_{n}} + \varepsilon_{n} \\
  \implies & \\
  & \forall \sum\limits^{\infty}_{n=1} \varepsilon_{n} = \varepsilon > 0: ~ \exists \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) \in D: ~ \sum\limits^{\infty}_{n=1}\sum\limits^{\infty}_{s=1} l(I^{n}_{s}) < \sum\limits^{\infty}_{n=1} \inf{D_{n}} + \varepsilon
  \end{align*}
  \]

所以：

所以：

Theorem 7.5 (Translation invariant - 平移不变性)

对于 \(\forall A \subset \mathbb{R}: ~ \forall t \in \mathbb{R}: ~ m^{*}(A) = m^{*}(A + t)\)，其中 \(A + t = \left\{ a + t: ~ \forall a \in A \right\}\)

Proof. (Theorem 7.5)

对于 \(\forall A \subset \mathbb{R}: ~ \forall t \in \mathbb{R}\)，令：

由满射确定 \(m^{*}(A)\) 的原象：

令：

由于 \(I_{n} + t = \left\{ i_{n} + t: ~ i_{n} \in I_{n} \right\}\) ，\(I_{n}\) 为区间，则 \(I^{'}_{n} = I_{n} + t\) 也为区间。

令 \(I_{n}\) 的左端点为 \(a_{n}, b_{n}\)，则 \(I^{'}_{n}\) 的左右端点为 \(a_{n} + t, b_{n} + t\)，则：

并且，如果 \(A \subset \bigcup\limits^{\infty}_{n=1}I_{n}\)，则

又因为：

则：

反之可证：若 \(A + t \subset \bigcup\limits^{\infty}_{n=1} I^{'}_{n}\)，则 \(A \subset \bigcup\limits^{\infty}_{n=1} I_{n}\)， 则：

所以二者下确界也相等，所以：