开路
数位 dp 开路
1. 每个 \(a_i\in [l_i,r_i]\) —— 维护极长不顶上下界连续段技巧
数位 dp 过程中,如果发现相邻两个数相同时最优,则可以设每个位置为 0/1/2 代表其 顶上界/顶下界/两者都不顶,于是极长 2 连续段的贡献由于可以任选易于计算, 于是记录 \(f(i,j,l,r,u)\) 表示 2 区间为 \([i,j]\),其中 \(i\) 位置高位情况为 \(l\),\(j\) 位置高位情况为 \(r\),当前位上右端点为 \(u\),进行转移。用区间 dp,每次将左边一段新区间和右边一段旧区间合并,时间复杂度 \(O(n^3\log V)\)。
树形 dp 开路
1. 关于包含一个点的连通块性质 dp —— dfs 序前后缀背包合并技巧
考虑点分治,那么令 \(f(i,j)\) 表示 dfs 序在 \(u\) 前,选 \(j\) 个点的 dp 值,令 \(g(i,j)\) 表示 dfs 序在 \(u\) 后,选 \(j\) 个点的 dp 值,转移方程为 \(f_(i,j)\rightarrow f(i+siz_u,j)\) 以及 \(f_(i,j)\rightarrow f(i+1,j+1)\),前者表示 \(u\) 这个点及其子树都不选,后者表示至少选了 \(u\)。\(g\) 的转移需要被动转移,方程类似。注意这里 \(f\) 不考虑 \(u\) 的贡献,\(g\) 考虑 \(u\) 的贡献(而不钦定选或不选),因此对 \(u\) 计算答案时直接将背包 \(f\) 和 \(g\) 合并即可。
奇怪操作开路
1. 对于每次最小元素有关的技巧
可以每次只考虑 \(\le k\) 的所有元素,忽略其余元素,从而收获一些有用的性质。
优化
图论优化
1. Dijikstra 相同边权点建虚点技巧
如果一张图中一个点 \(u\) 需要向若干个点连很多条边权相同的边,那么可以建一个虚点 \(w\),改为 \(u\) 向 \(w\) 连一条这个边权的边,然后视为 \(w\) 向这一堆点连边权为 \(0\) 的边,只把 \(w\) 塞进堆里。当将 \(w\) 弹出时,由于 \(w\) 连出的边边权均为 \(0\),因此 \(w\) 所连向的这些点可以不用塞进堆而是立即赋为 \(dis_w\) 并更新其他点。可以用数据结构加速找点的过程。
2. 交互题/通信题卡次数技巧
在我们运用人类智慧推出一车性质最终被卡 1~2 步次数时,一定要记得可以在小范围内使用 dp 进行决策! 往往较小的范围才会出问题,并且也省去了许多大力分讨的过程。
时间复杂度证明
1. 基于势能观察的时间复杂度证明
尝试对一个东西进行不断的调整直至合法,可以考虑构造一个势能 \(\varphi\),每花 \(T\) 的时间该势能会减 \(\varphi\),则这个不断调整的时间复杂度至多为 \(\varphi\)。
计数
多项式科技
1. \(O(n^2)\) 相邻位置 dp 转移技巧
对于 \(f(i-1,j)\) 转移到 \(f(i,j-1),f(i,j),f(i,j+1)\) 的问题,可以将其转化成 $F\rightarrow F\cdot (ax+b+cx^{-1}) $ 的形式。发现最终的答案会形如 \(G_0F+G_1f_1[0]+G_2f_2[0]+\dots\) 的形式,其中 \(f_i[0]\) 表示第 \(i\) 次做完乘法之后的结果。考虑分治,计算每次乘完之后的 \(f[0]\) 然后再做一遍分治 NTT 即可。考虑计算区间 \([l,r]\) 中的答案,发现只有 \(x^{-(mid-l+1)}\dots x^{mid-l+1}\) 会对 \([l,mid]\) 中的 \(f[0]\) 产生影响。 于是可以拎出这部分的多项式递归下去处理,时间复杂度 \(O(n\log^2n)\)。尚未实现
构造
证明成立
1. 证明图中不存在环的势能法
考虑对图 \(G\) 定义一个势能 \(\varphi(G)\),然后尝试证明如果 \(G\) 中存在环,那么令 \(G\) 以某种方式消环之后的结果为 \(G'\),并尝试证明 \(\varphi(G')<\varphi(G)\),如果成功,那么我们只需求出 \(\varphi(G)\) 最小的 \(G\) 即可。
建模
转化
1. 曼哈顿距离转切比雪夫距离技巧
将坐标 \((x,y)\) 转化为 \((x+y,x-y)\) 之后,原先的曼哈顿距离变为 \(\max (|x_1-x_2|,|y_1-y_2|)\),在最优化问题中,后者可以拆开,让每个点的贡献为 \(\pm x\) 或 \(\pm y\)。
2. 大小关系转 01 序列技巧
对于只和数与数之间的大小有关的序列及其操作题目,可以考虑枚举阈值 \(x\) 后转 01 序列并用数据结构维护。由于某个特定的 \(x<y\) 在转化后必然会在某个阈值时在 01 中显现出来, 因此这样做是对的。
网络流
1. 模拟费用流——中间一排点数较少
可以对于中间每两个点(以及源汇)之间维护一个优先队列表示所有边的权值 (由于这些点必然被经过),然后每次增广的时候只需要关心堆顶的边权的值,于是每次增广的复杂度是 \(O(1)\) 的(虽然常数有点大),然后将边反向的时候也最多改变 \(O(1)\) 次优先队列。
2. 若干物品每种物品选一种属性的技巧
最小割模型,从 \(S\) 到 \(T\) 拉出 \(n\) 条链代表 \(n\) 个物品,链的长度(边数)为 \(m\),断掉第 \(i\) 条链中的第 \(j\) 条边代表第 \(i\) 个物品选第 \(j\) 种属性。注意可以从 \((i,j)\) 向 \((i,j-1)\) 连一条 \(+\infty\) 流量的边防止一条链被断两次,详见 这里
3. 最小割模型由式子建边技巧
对于一种建模,可以列出许多 \(01\) 变量,注意每个代价形如 \(ax_i\),\(b\overline{x_i}\) 或 \(cx_i\overline{x_j}\),这样就可以对于每个变量 \(x_i\) 建一个点并处理 \(x_i\) 与 \(x_j\) 之间的连边了。
4. 每个点选黑色或白色,一个点的颜色受其它点限制贡献的技巧
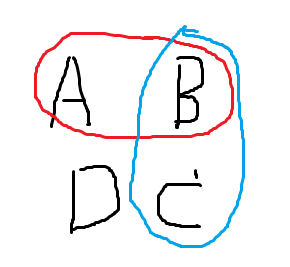
以 BZOJ 3218 a+b problem 为例,每个黑点受是否在 \(S_i\) 中有白点而是否产生 \(p_i\) 的贡献。正确连边如下图所示,连 \(S\) 代表黑点,连 \(T\) 代表白点,题目求最大价值,因此答案为 \(W-\) 最小割:
分四类情况讨论:
- \(u\in S,u'\in S\):此时 \(p_u\) 不用割,因此产生 \(p_i\) 的贡献;
- \(u\in S,u'\in T\):此时 \(p_u\) 必须割,失去的 \(p_i\) 的贡献,注意此时边 \((u',u)\) 并不影响;
- \(u\in T,u'\in S\):此时由于 \((u',u)\) 的存在,不合法;
- \(u\in T,u'\in T\):此时 \(p_u\) 也必须割,失去的 \(p_i\) 的贡献。
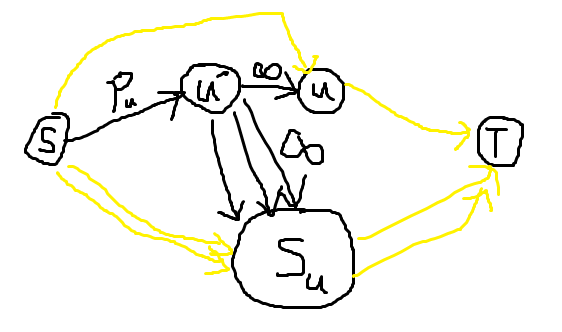
(如果一个黑点受 \(S_u\) 中是否有黑点而是否产生贡献,则可以考虑变成不用割 \((u',u)\) 会产生贡献,即代价为最小割而非 \(W-\) 最小割。)
5. 网络流边权解方程技巧
发现想用最小割而发现容量可能为负,或者想用最小费用最大流而发现费用无法确定,可以通过枚举所有情况并解方程得出每条边的正确边权。
例题:Uoj336 无限之环 要求旋转右边的水管使得整张图不漏水。

直接分类讨论,其中第一类要求中间的点拆成两个相对的各选一个,第三个 trivial,重点在第二个。
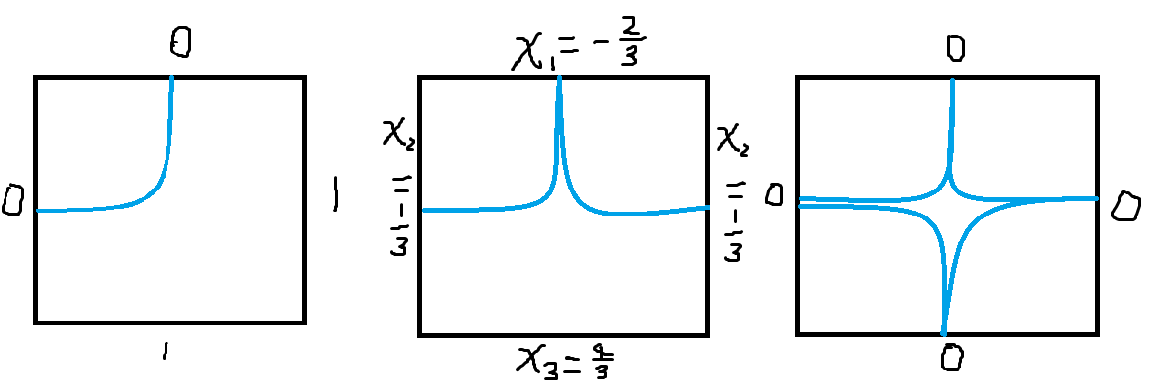
这个结果实际上是解方程解出来的,实现上可以所有流量 \(\times 3\) 即可:
x_1+2x_2=0\\
x_1+x_2+x_3=1\\
x_3+2x_2=2
\end{cases}
\Longrightarrow
\begin{cases}
x_1=-2/3\\
x_2=1/3\\
x_3=4/3
\end{cases}
\]