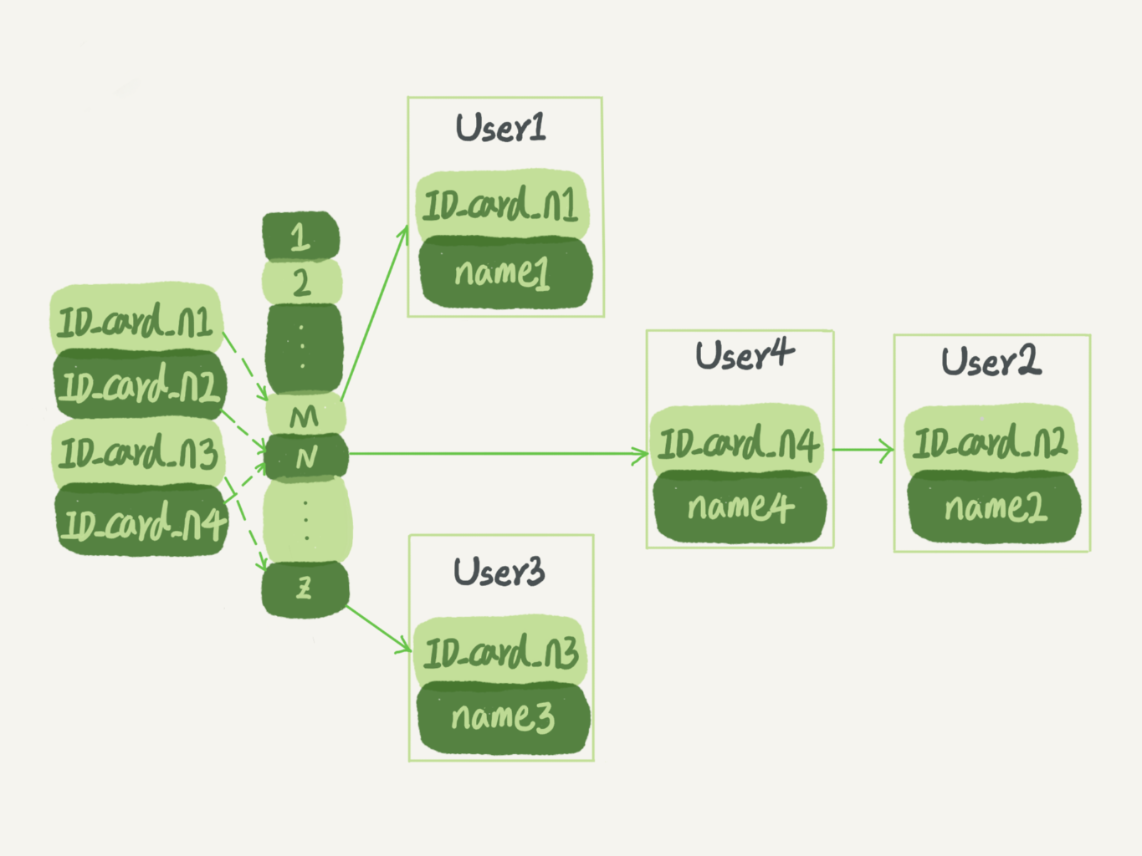
很多人都听说过汉诺塔问题，这是来源于印度的古代游戏。一个板子上有三根柱子以及一些大小和颜色各不相同的圆盘。我们分别把这三根柱子叫做起始柱A、辅助柱B已经目标柱C，游戏的要求如下：

把起始柱A上所有的圆盘都移动到C柱，且在移动过程中始终保持圆盘从小到大排列，即大盘在下、小盘在上。

移动过程中可以把盘子放在A、B、C任意一杆上。

场景如图所示：

由于盘子的数量是不固定，数量越大，越难直接分析出每个步骤。所以需要把问题简化到我们可以分析的程度，然后找到算法来解决。如果存在某种规律，那么可以考虑用递归来解决问题了。

从最简单的情况开始分析，如果圆盘数量只有1个，那么步骤非常简单：

把圆盘从A柱移动到C柱。过程如图所示。

如果是2个盘子，那么需要三步：

1.先把最上面的小盘子从A移动到辅助柱B，

2.然后把最大的盘子从A移动到C。

3.然后把最小的盘子从B移动到C。

如图所示，一共三步。

到目前为止没发现什么规律，需要进行增加盘子。

当盘子数量变成3，则步骤变多了。经过实验，如下：

1.把盘子从A移动C。

2.把盘子从A移到B。

3.把盘子从C移到B。

4.把盘子从A移动到C。

5.把盘子从B移动到A。

6.把盘子从B移动到C。

7.把盘子从A移动到C。

发现了一些规律，假设一共要转移N个盘子（N大于0，且为正整数）：

1. 每次都是先把除了最后一个盘子之外的盘子，也就是N -1个盘子先从起始柱A移动到了辅助柱B。
2. 然后把最后一个盘子直接从起始柱A移动到目标柱C。
3. 把N-1个盘子从辅助柱B移动到目标柱C。

通过重复将问题分解为同类的子问题而解决问题的方法，我们找到了递归终止的条件，就是当N等于1。

于是可以开始写代码了，JS实现如下所示：

/**
 * The solution of the hanoi question
 * 
 * @param {number} num  the number of the disks
 * @param {string} source  start bar name
 * @param {string} buffer  auxiliary bar name
 * @param {string} target  target bar name
 * @returns 
 */
function hanoi(num, source, buffer, target) {
    // When the num is 1, we can move the disk from source to target directly
    if (num === 1) {
        console.log(`Move the disk from ${source} to ${target}`);
        return;
    }

    // move source to buffer
    hanoi(num - 1, source, target, buffer);
    // move 1 from source to target
    hanoi(1, source, buffer, target);
    // move num - 1 from buffer to target
    hanoi(num - 1, buffer, source, target);
}

测试一下三个盘子的情况，结果输出如下：

Move the disk from A to C
Move the disk from A to B
Move the disk from C to B
Move the disk from A to C
Move the disk from B to A
Move the disk from B to C
Move the disk from A to C

对于递归问题，最重要的是找到递归终止条件和递推函数，也要注意有时候递归深度太大，会导致性能问题。征服汉诺塔问题，我们也同时弄懂了如何用好递归。