参考题解地址

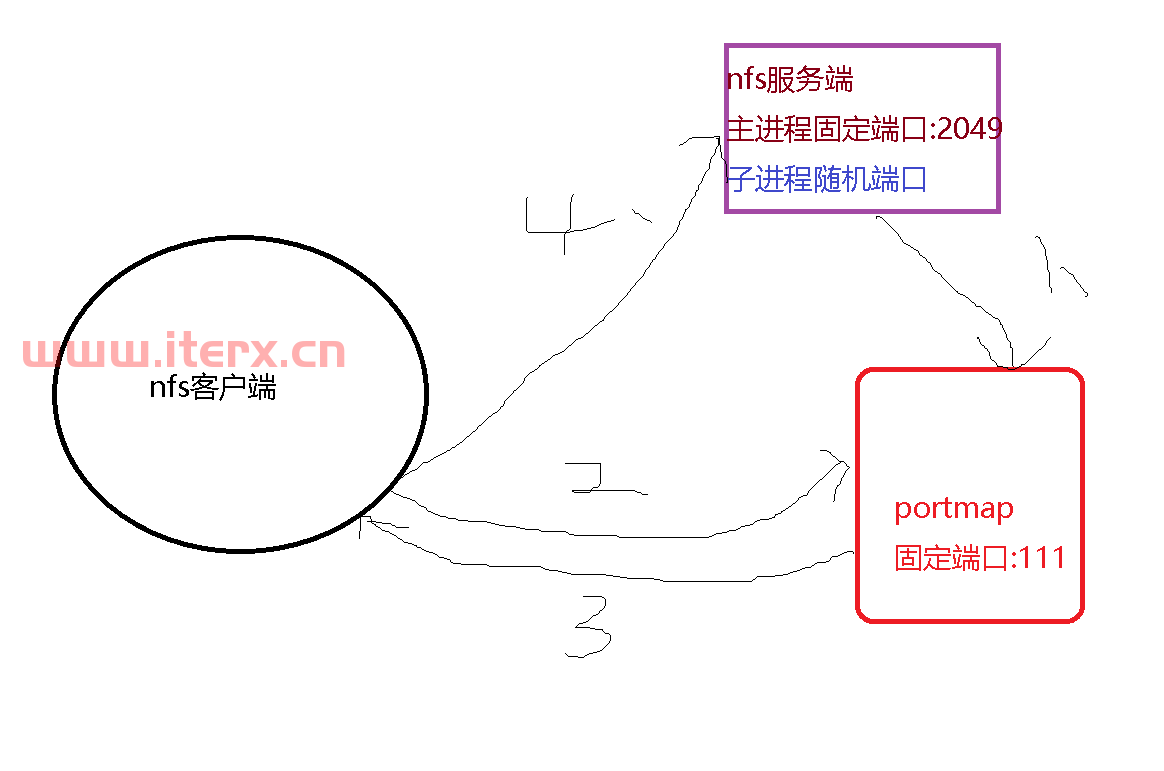
1. 从树上任意一个节点开始，跳到其随机一个后代，跳到叶子的期望次数为 \(H_{siz_u}=\ln(siz_u)\)。

证明：
首先考虑一条链的情况。设在第 \(i\) 个点期望次数为 \(a_u\)，\(\{a\}\) 的前缀和为 \(\{S\}\)，那么就有 \(a_u=1+\frac{S_{u-1}}{u-1}\)。

\[a_u=1+\frac{S_{u-1}}{u-1}\\
(u-1)a_u=u-1+S_{u-1}\\
ua_{u+1}=u+S_u\\
ua_{u+1}-(u-1)a_u=a_u+1\\
a_{u+1}=a_u+\frac 1 u\\
a_u=H_{u-1}
\]

（注意调和级数的 \(\ln\) 不带常数）
对于非链的树，随便挑一个叉出去的子树接到一个叶子下面，显然每个节点的期望步数增加，总步数增加。于是链是最坏的情况，证毕。

2. 对于任意一棵树，可以将其划分成 \(O(\log)\) 层叶链，每层叶链定义为剥出叶子及其向上跳最远使得沿途节点只有一个儿子的链。

证明：
设 \(T(u)\) 为节点 \(u\) 被删的时间，则若 \(u\) 的儿子 \(v\) 中 \(T(v)\) 最大值唯一，则 \(T(u)=T(v)\)，否则 \(T(u)=T(v)+1\)。
不难归纳证明使得 \(T(u)\ge k\) 时 \(siz_u\ge 2^k-1\)，证毕。

3. 对于一棵树的任意一种点分形式（不一定选重心），记一次分治的代价为分出的所有非最大子树的 \(siz\) 之和，则总代价为 \(O(n\log n)\)。

证明：
考虑每个点的贡献，每当它对代价产生贡献时 \(siz\) 一定翻倍，于是显然贡献之和为 \(O(n\log n)\)。